Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the inflection points of a function of one variable
ResourceFunction["InflectionPoints"][expr, x] computes the inflection points of the expression expr with respect to variable x. | |
ResourceFunction["InflectionPoints"][{expr,constraint},x] computes the inflection points expr, subject to the given condition constraint on x. | |
ResourceFunction["InflectionPoints"][…, "Properties"] computes the inflection points of a function, along with function properties at these points. |
Find the inflection points of a cubic function:
| In[1]:= |
| Out[2]= |
Plot the function and its inflection points found above:
| In[3]:= |
| Out[3]= | 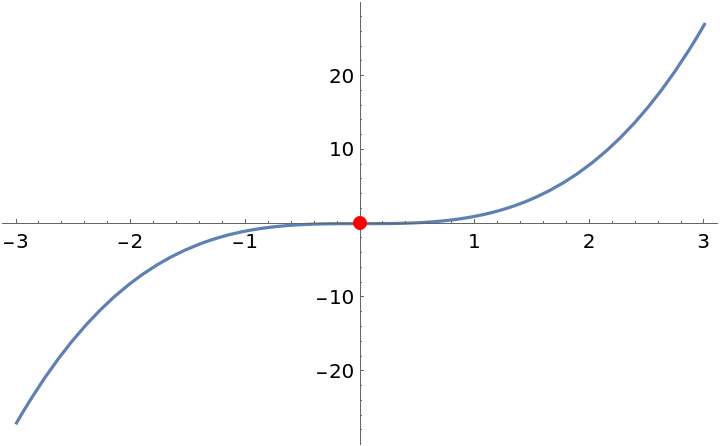 |
Repeat the calculation, classifying inflection points:
| In[4]:= |
| Out[4]= |
Find and classify the inflection points of a polynomial function:
| In[5]:= |
| Out[6]= |
Plot the function and its inflection points:
| In[7]:= |
| Out[7]= | 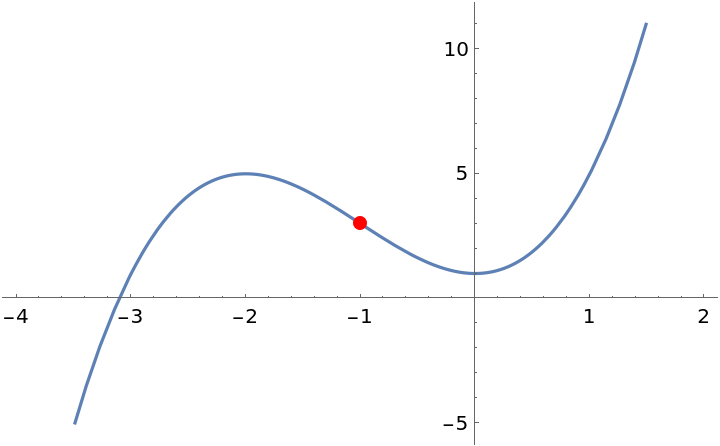 |
Find and classify the inflection points of another polynomial function:
| In[8]:= |
| Out[9]= |
Plot the function and its inflection points:
| In[10]:= |
| Out[10]= | 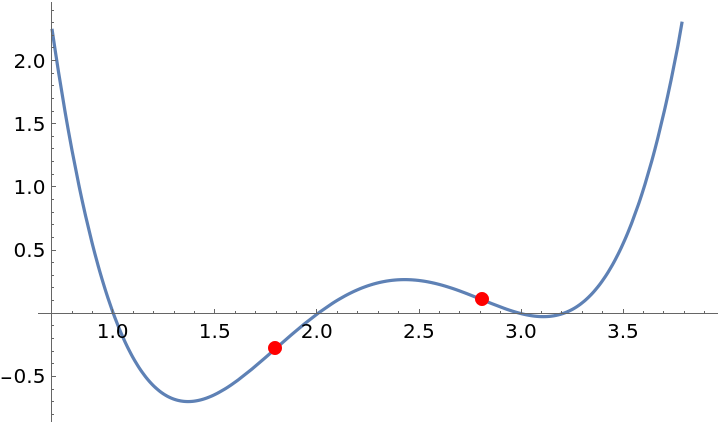 |
Find and classify the inflection points of a trigonometric function:
| In[11]:= |
| Out[12]= |  |
Plot the function and a single cycle's worth of its inflection points:
| In[13]:= |
| Out[13]= | 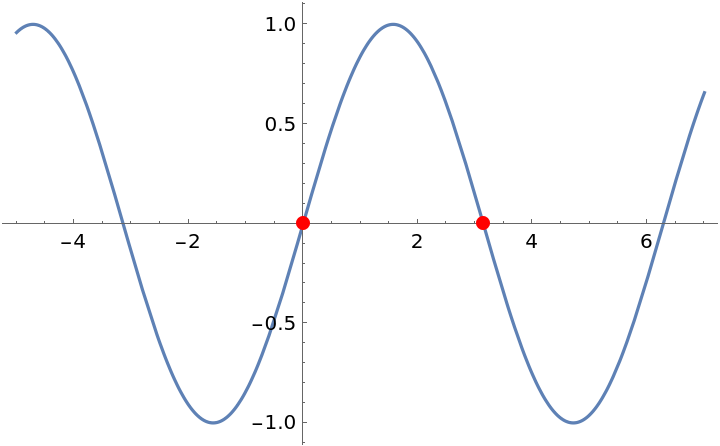 |
Find and classify the inflection points of a function, specifying the range of the independent variable to include:
| In[14]:= |
| Out[15]= |  |
Plot the function and its inflection points:
| In[16]:= |
| Out[16]= | 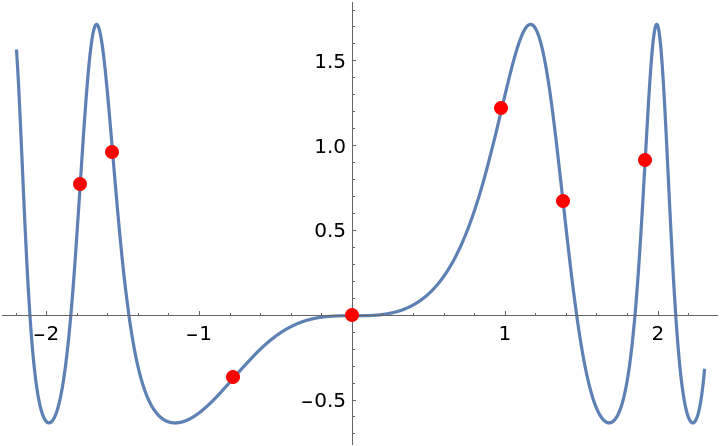 |
InflectionPoints will sometimes return results in terms of Root objects:
| In[17]:= |
| Out[18]= |
Applying N to these outputs converts to an ordinary numeric result:
| In[19]:= |
| Out[19]= |
Plot the function and its inflection points:
| In[20]:= |
| Out[20]= | 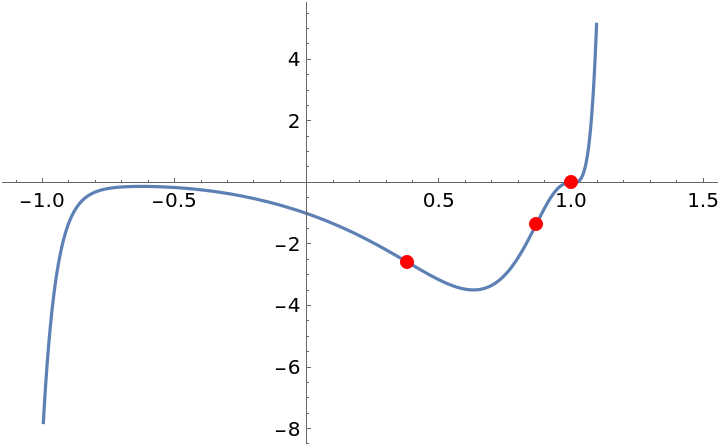 |
For functions with a repeating pattern of inflection points, InflectionPoints returns results in terms of one or more undetermined constants, which can take any integer value:
| In[21]:= |
| Out[22]= |  |
Plot the function and a single period's worth of its inflection points:
| In[23]:= |
| Out[23]= | 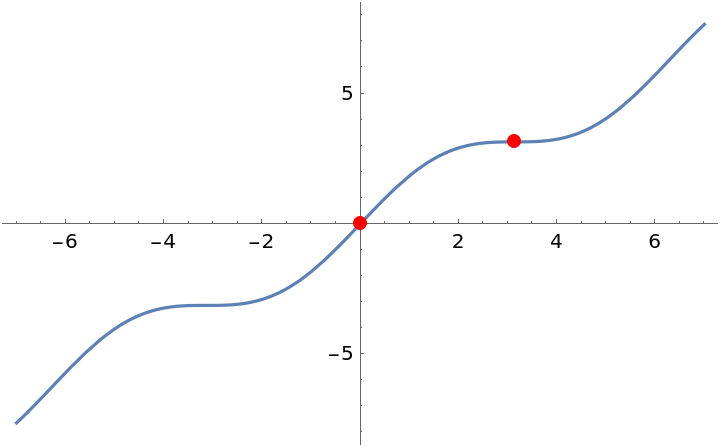 |
Find the inflection points of another periodic function:
| In[24]:= |
| Out[25]= |  |
Plot the function and a single cycle's worth of its inflection points:
| In[26]:= |
| Out[26]= | 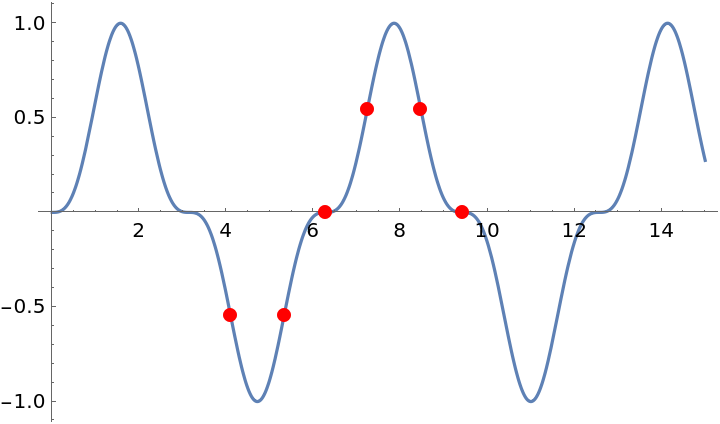 |
This work is licensed under a Creative Commons Attribution 4.0 International License