Basic Examples (3)
Decompose 25 as a sum of powers of 3 and 4:
Expand 7, 11 and 13 to the twentieth power and take the sum:
Recover the representation of this sum using bases 7, 11 and 13:
Get a random integer:
Express it as a sum of powers of 7, 11 and 13:
Confirm the result:
Scope (6)
InactiveSumOfPowers works with negative numbers:
InactiveSumOfPowers[0,…] works with both non-List and List second arguments. In the prior case, InactiveSumOfPowers[0,q] returns an Inactive version of Power[q,-Infinity]:
In the latter case, InactiveSumOfPowers[0,{a1,…,an}] returns an Inactive form of Power[a1,-Infinity]+⋯+Power[an,-Infinity]:
InactiveSumOfPowers[Infinity,…] and InactiveSumOfPowers[-Infinity,…] both work as expected. Here are some computations with Infinity:
Here are some with -Infinity:
Both Infinity and -Infinity work as elements of first-argument lists as well:
InactiveSumOfPowers[list1,list2] threads over list1 and equals InactiveSumOfPowers[#,list2]&/@list1:
In all cases, the the Inactive output equals the input when activated:
InactiveSumOfPowers[list,q] threads over list when q is an Integer:
Confirm the results:
InactiveSumOfPowers[list] is equivalent to InactiveSumOfPowers[list,2]:
Options (8)
CollectLikeTerms (2)
With "CollectLikeTerms"->False (the default), repeated terms remain uncombined:
With "CollectLikeTerms"->True, repeated terms are combined together:
In both cases, the activated version of the output equals the input:
If no like terms are produced during the decomposition, "CollectLikeTerms"->True has no effect on the output:
FactorNegative (3)
Given an input n<0, InactiveSumOfPowers[n,…] produces negative signs in the output. Setting "FactorNegative"->False (the default) specifies that each term in the sum is made negative:
With "FactorNegative"->True, a single negative is "factored out" of the sum so the individual summands remain positive:
In both cases, the activated version of the output equals the input:
HoldListProducts (3)
If n is a product of powers of the elements of list, then the output of InactiveSumOfPowers[n,list,…,"HoldListProducts"->True] will be an Inactive factorization of n. This uses the resource function InactiveFactorInteger in the backend:
Conversely, using "HoldListProducts"->False (the default) will result in the usual decomposition:
In both cases, the activated version of the output equals the input:
Applications (7)
InactiveSumOfPowers[n,q] can be used to mimic the output of BaseForm[n,q]. First, define a random n and q:
Apply InactiveSumOfPowers:
Strip away the excess and see which powers are present and which are missing in the sum:
Use Tally to figure out how many copies of each term exist inside the sum (including the ones with coefficient 0):
Now, collect the data:
Apply BaseForm to it:
The result is effectively the same as BaseForm[n,q]:
Properties and Relations (4)
Define an integer:
Express it as the sum of powers of 4:
Confirm the result:
The same result can be achieved using {4} as a second argument instead of 4:
Define a new (large) integer:
Express it as the sum of (many) powers of 2 using a two-argument form and use Shallow to show a small snippet of the result:
The same can be achieved using the one-argument form:
Confirm the results:
If n is a product of powers of the elements of list, then the output of InactiveSumOfPowers[n,list,…,"HoldListProducts"->True] will be an Inactive factorization of n:
This is equivalent to the result returned by the resource function InactiveFactorInteger:
It is also equivalent to the result returned by the resource function FormatFactorization, though the latter is formatted differently:
The equivalence of all three forms can be verified with a combination of Activate and ReleaseHold:
If a single base is given then InactiveSumOfPowers is equivalent to IntegerDigits:
Compare to the result of IntegerDigits with some post-processing to show explicit powers:
Possible Issues (3)
InactiveSumOfPowers remains unevaluated for a number of input types. The first element must be an integer, a List of integers, Infinity or -Infinity:
If the second argument is a List, all of its elements must be integer quantities greater than 1:
The main use case for defining this function originally was to write a given integer as a sum of powers of primes. For example, this will express Factorial2[25]=7905853580625 as the sum of powers of 5 and 7:
Given complicated sums like this, collecting like terms is a natural desire. As such, the functionality for "CollectLikeTerms"->True was built in:
The outcome is that factorial2b now has coefficients which are no longer in the list {5,7} of desired bases. Here are the coefficients not in the list {5,7}:
This is a desired outcome of the algorithm, but it could ostensibly be an issue for some users.
Regardless of what is chosen for "HoldListProducts", InactiveSumOfPowers[p1n1p2n2⋯pknk,list,…] results in the usual decomposition if any factor pi is not present in list. This is because the algorithm used in InactiveSumOfPowers looks for list to contain all of the pi when considering whether n=p1n1p2n2⋯pknk is a "list product":
On the other hand, if list contains all of the factors p1,p2,…,pk plus additional items, "HoldListProducts"->False returns a different (though equivalent) factorization than "HoldListProducts"->True:
Neat Examples (3)
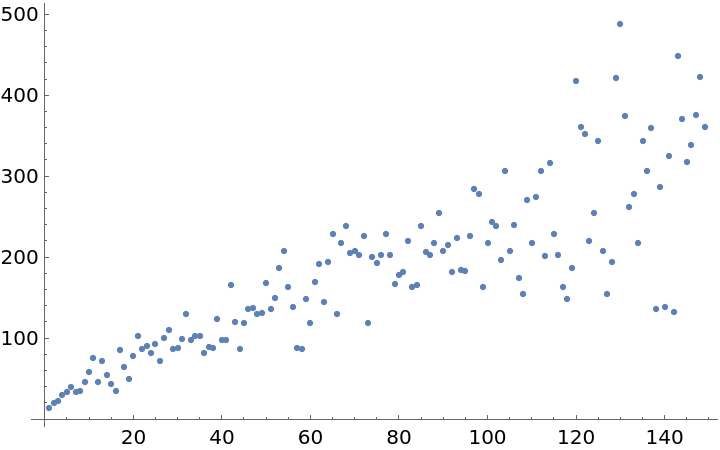
As n increases, the number of terms in InactiveSumOfPowers[n] displays an interesting quasi-periodic pattern. First, compute the lengths:
Plot the values to observe the pattern:
For fixed n, the number of terms in InactiveSumOfPowers[n,m] tends to increase as m increases. First, declare a (large-ish) integer:
Compute the lengths:
Plot them:
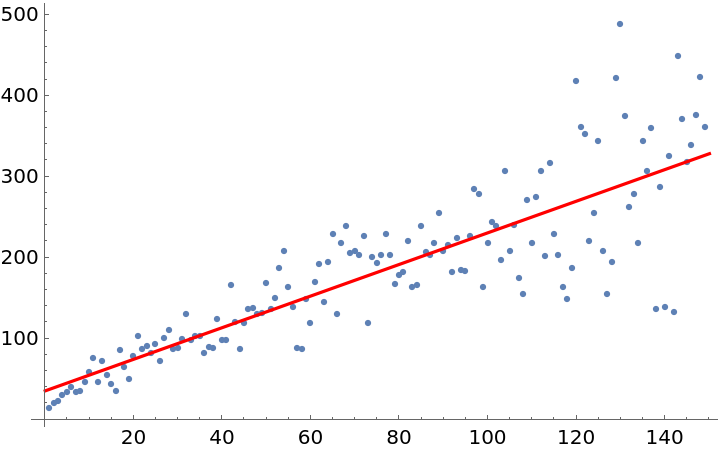
The growth appears to be roughly linear. Test that observation:
Check the goodness of fit, visually:
Check the goodness of fit mathematically as well:
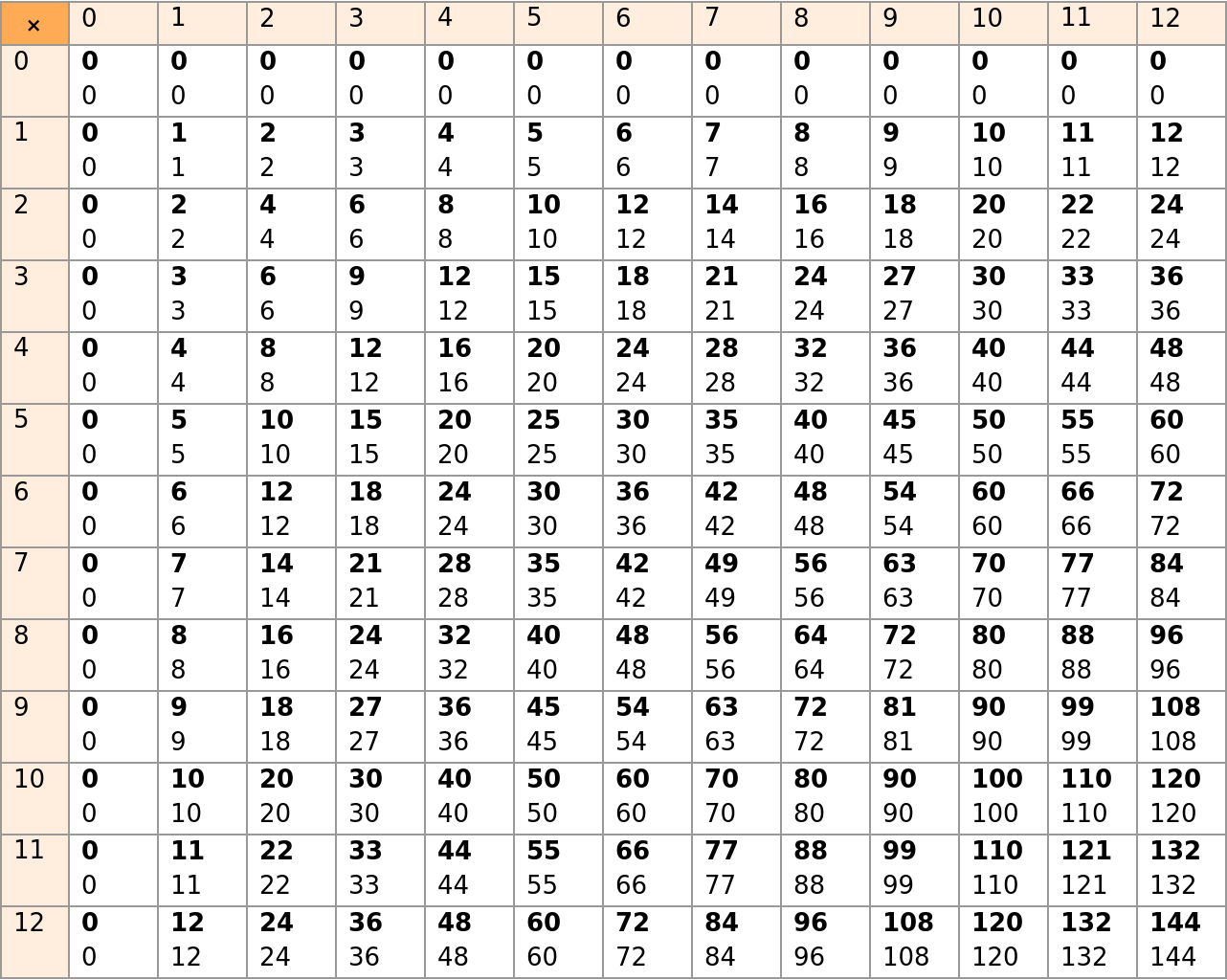
Create a multiplication table where InactiveSumOfPowers (and a little formatting) has been applied to each product. First, create the data:
Then, display a stylized version of the table:
Check the activated version for correctness:
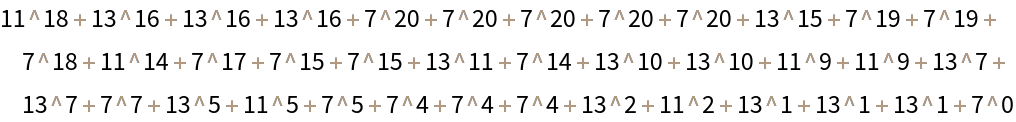
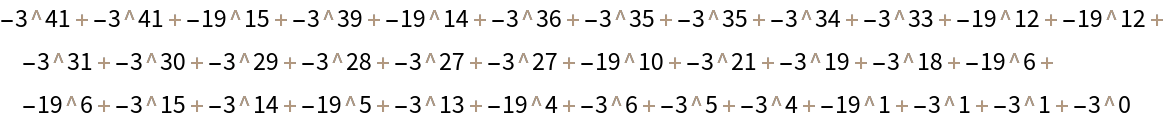
![Join[{{Style["input", Bold], " ", Style["decomp", Bold], " ", Style["equal?", Bold]}}, {Activate[#], " ", #, " ", Activate[# == #]} & /@ ResourceFunction[
"InactiveSumOfPowers"][{75, -Infinity, -91, Infinity, 0}, Fibonacci /@ Range[3, 7]]] // Grid[#, Dividers -> {False, All}, FrameStyle -> Dotted] &](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/3a97081d467fdf91.png)
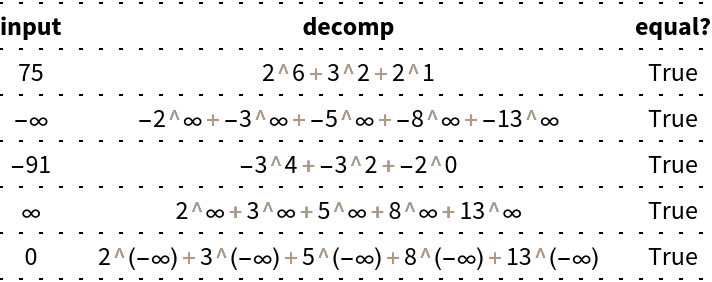
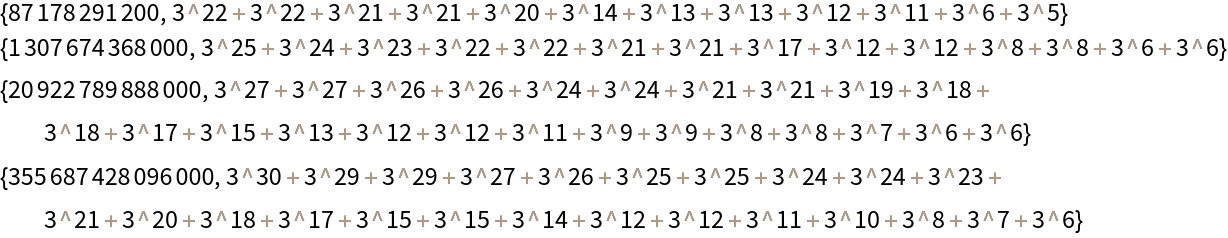
![Grid[{#, ResourceFunction["InactiveSumOfPowers"][#, 3], If[Activate[ResourceFunction["InactiveSumOfPowers"][#, 3] == #], "They're equal!", "Oh no!"]} & /@ Factorial[Range[14, 17]], Frame -> All, ItemSize -> {{10, Automatic, 10}}]](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/33fd7d3763e4ec3b.png)
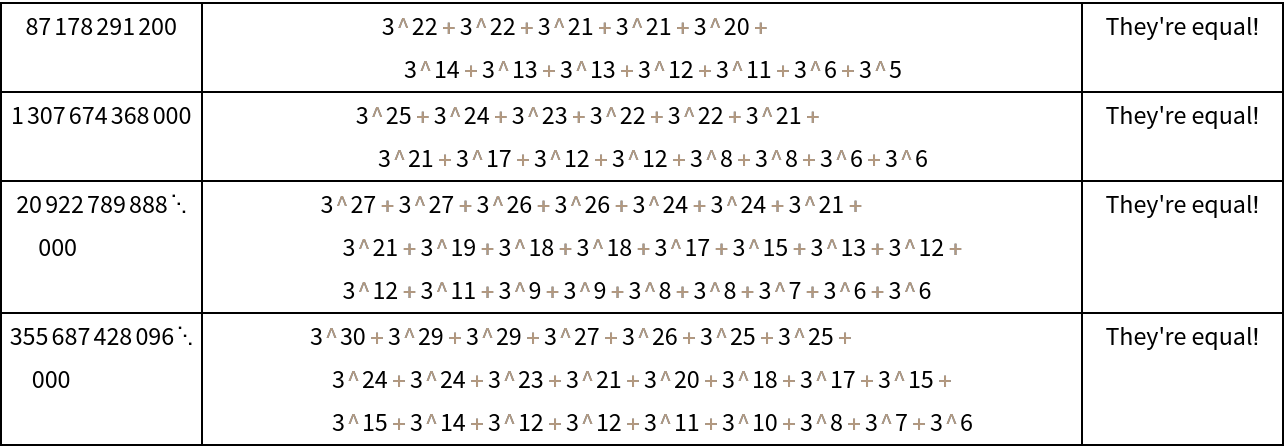
![{ResourceFunction["InactiveSumOfPowers"][#], If[Activate[
ResourceFunction["InactiveSumOfPowers"][#] == ResourceFunction["InactiveSumOfPowers"][#, 2]], "equals", "is saddened by"], ResourceFunction["InactiveSumOfPowers"][#, 2]} & /@ Prime[Range[Factorial[11], Factorial[11] + 3]] // Grid[#, Frame -> All] &](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/707817fbefdd2f47.png)

![Activate[ResourceFunction["InactiveSumOfPowers"][32123, 17]] == Activate[
ResourceFunction["InactiveSumOfPowers"][32123, 17, "CollectLikeTerms" -> True]] == 32123](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/575f802c622e74dc.png)
![Activate[ResourceFunction["InactiveSumOfPowers"][-2047, 2]] == Activate[
ResourceFunction["InactiveSumOfPowers"][-2047, 2, "FactorNegative" -> True]] == -2047](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/77b9e45faa06434d.png)
![Activate[
ResourceFunction["InactiveSumOfPowers"][2^9*3^15*5, {2, 3, 5}]] == Activate[
ResourceFunction["InactiveSumOfPowers"][2^9*3^15*5, {2, 3, 5}, "HoldListProducts" -> True]] == 2^9*3^15*5](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/681599d6e9a0bc60.png)
![realtally = ReverseSortBy[
Join[firsttally, Transpose[{missingpowers, ConstantArray[0, Length[missingpowers]]}]], First]](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/1fe1b9ca5645edd0.png)
![Activate[
ResourceFunction["InactiveSumOfPowers"][4^9*7^15*71, {2, 7, 71}, "HoldListProducts" -> True]] == Activate[ResourceFunction["InactiveFactorInteger"][4^9*7^15*71]] == Activate[
ReleaseHold[ResourceFunction["FormatFactorization"][4^9*7^15*71]]]](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/733d3dfc5c5dd44d.png)

![Show[{
ListPlot[lengths],
Plot[lm[x], {x, 0, 150}, PlotStyle -> Red]
}]](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/51c8a95d1d4360c8.png)
![nums = # & /@ Table[Times[i, j], {i, 0, 12}, {j, 0, 12}] /. {a_Integer :> Style[a, FontWeight -> Bold]};
sums = ResourceFunction["InactiveSumOfPowers"][#, {2, 3}] & /@ Table[Times[i, j], {i, 0, 12}, {j, 0, 12}];
table = Table[
Transpose[{%%[[i]], %[[i]]}], {i, 1, 13}] /. {List[Style[a_Integer, Rule[FontWeight, Bold]], b_] :> Column[List[Style[a, Rule[FontWeight, Bold]], b]]};](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/26e25bd10d195093.png)
![fulltable = TextGrid[
Join[{Join[{Item[Style["\[Times]", Larger], Background -> Lighter@ Orange, Alignment -> Center]}, Table[i, {i, 0, 12}]]}, MapIndexed[Prepend[#1, First[#2] + 0 - 1] & , table]],
Frame -> All, FrameStyle -> Directive[GrayLevel[0.6]], Background -> {1 -> Lighter@LightOrange, 1 -> Lighter@LightOrange}, ItemSize -> {{{2, ConstantArray[13, 13] /. {List -> Sequence}}}}, Alignment -> {Left, Top}, Spacings -> {1, Automatic}]](https://www.wolframcloud.com/obj/resourcesystem/images/bc0/bc07831b-983a-41e6-8e1d-8f34abef9ff0/68c47606b0a586a5.png)