Function Repository Resource:

InShuffle

Source Notebook

Perform an in shuffle on a list

Contributed by: Sander Huisman

ResourceFunction["InShuffle"][list]

performs an in shuffle on list.

ResourceFunction["InShuffle"][list,n]

performs n in shuffles on list.

Details and Options

An in shuffle is defined as follows: (1) split the list in two halves; and (2) interweave each half of the list starting with the second half, such that every other card came from the same half of the original list.

Here is an example of a list with 10 items:

When a list has an odd length n, the first "half" will be (n-1)/2 long and the second "half" will be (n+1)/2 long:

Examples

Basic Examples (1)

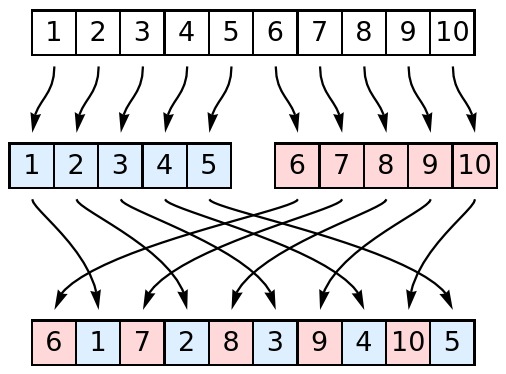
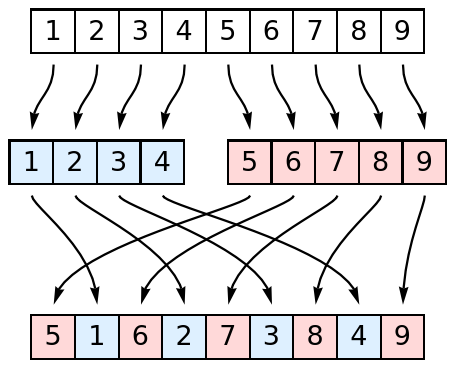
Perform an in shuffle on a list of 10 items:

In[1]:=

Out[1]=

Scope (2)

Perform an in shuffle 3 times to a list:

In[2]:=

Out[2]=

Confirm that this is the same:

In[3]:=

Out[3]=

The list can contain expressions of different type:

In[4]:=

Out[4]=

Applications (3)

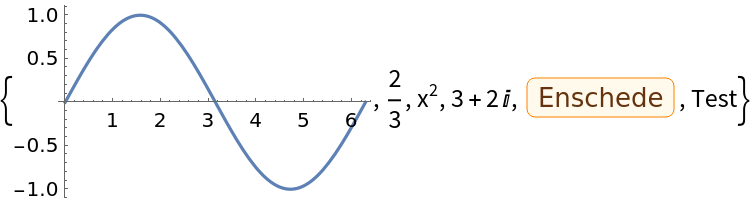Create a sorted deck of cards:

In[5]:=

$deck = StringJoin@*Reverse /@ Tuples[{{"\[SpadeSuit]", "\[HeartSuit]", "\[DiamondSuit]", "\[ClubSuit]"}, Join[{"A"}, ToString /@ Range[2, 10], {"J", "Q", "K"}]}]$

Out[5]=

Shuffle the deck once:

In[6]:=

Out[6]=

The original is obtained after 52 shuffles:

In[7]:=

Out[7]=

Properties and Relations (3)

An in shuffle on a list of length 2 can be seen as swapping the elements or reversing the list:

In[8]:=

Out[8]=

Figure out after how many in shuffles a list of size n returns to its original order:

In[9]:=

For lists of even length, the number of shuffles to return to the original order is known analytically:

In[10]:=

Out[10]=

In[11]:=

Out[11]=

Visualize how the positions of items are changed for a list of length 21 in the form of a Graph:

In[12]:=

t = Range[21];
edges = Thread[t -> Ordering[ResourceFunction["InShuffle"][t]]];
Graph[edges, VertexLabels -> "Name"]

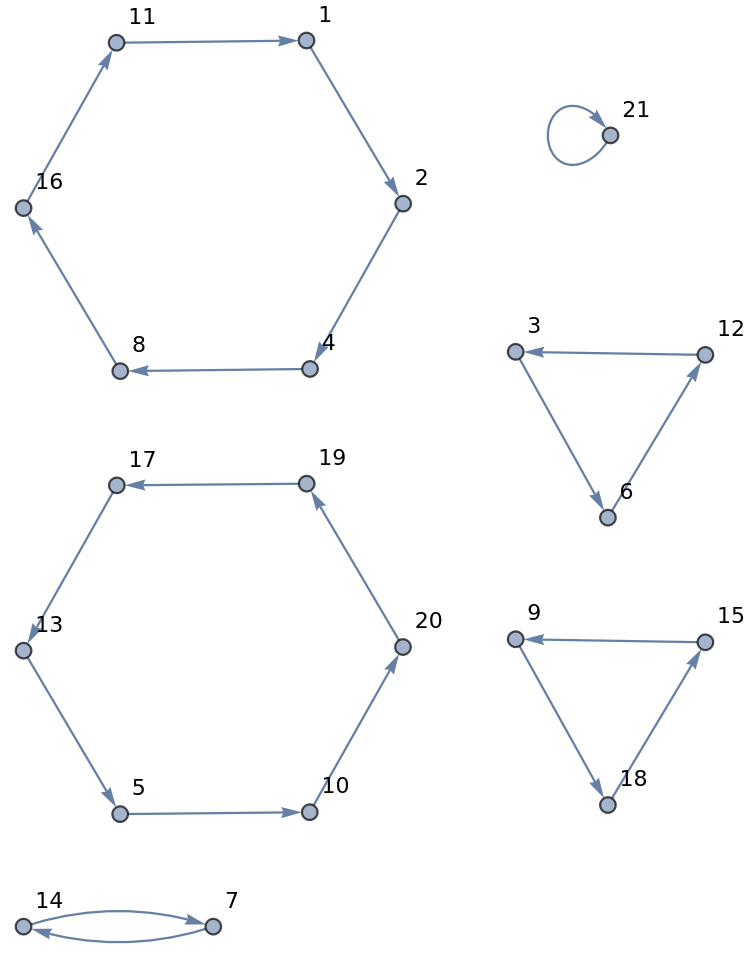
Confirm that 6 nested in shuffles returns the list of 21 items to the original order:

In[13]:=

t = Range[21];
edges = Thread[t -> Ordering[ResourceFunction["InShuffle"][t, 6]]];
Graph[edges, VertexLabels -> "Name"]

Possible Issues (1)

0 iterations returns the original list:

In[14]:=

Out[14]=

Neat Examples (1)

Plot how many in shuffles are needed to return to the original order for a list of length n:

In[15]:=

$howManyIterations[n_] := Length[NestWhileList[ResourceFunction["InShuffle"], ResourceFunction["InShuffle"]@Range[n], # =!= Range[n] &]] data = Table[{i, howManyIterations[i]}, {i, 1024}]; ListPlot[data, Frame -> True, FrameLabel -> {"L", "Number of shuffles needed"}, PlotRange -> All]$

Out[17]=

Publisher

SHuisman

Requirements

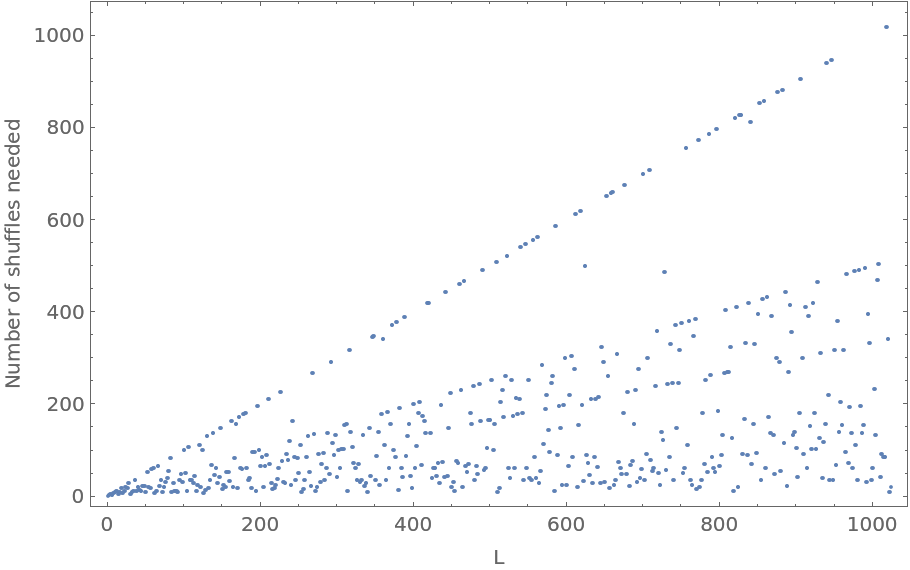Wolfram Language 11.3 (March 2018) or above

Version History

1.0.0 – 10 May 2019

Source Metadata

Citation:
- Conway, J. H. and Guy, R. K. "Fractions Cycle into Decimals." In The Book of Numbers. New York: Springer-Verlag, pp. 163-165, 1996.
  Diaconis, P.; R.L. Graham; W.M. Kantor (1983). "The mathematics of perfect shuffles" (PDF). Advances in Applied Mathematics. 4 (2): 175–196. doi:10.1016/0196-8858(83)90009-X.

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

InShuffle

Details and Options