Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ImplicitCurvature

Source Notebook

Compute the implicit curvature of a curve

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["ImplicitCurvature"][c,{x,y}]

computes the implicit curvature of a plane curve c with respect to variables x and y.

Details and Options

An implicit curve is a planar curve written using only two coordinate variables, such as x and y.

Examples

Basic Examples (2) 

Get the equation for a bow curve:

In[1]:=
bow = Entity["PlaneCurve", "BowCurve"][ EntityProperty["PlaneCurve", "AlgebraicEquation"]][a]
Out[1]=

Compute the implicit curvature:

In[2]:=
ResourceFunction["ImplicitCurvature"][ bow[x, y], {x, y}] // FullSimplify
Out[2]=

Get the equation for a cissoid of Diocles:

In[3]:=
cissoid = Entity["PlaneCurve", "DioclesCissoid"][ EntityProperty["PlaneCurve", "AlgebraicEquation"]][1]
Out[3]=

Compute the implicit curvature:

In[4]:=
imp = ResourceFunction["ImplicitCurvature"][cissoid[x, y], {x, y}] // FullSimplify
Out[4]=

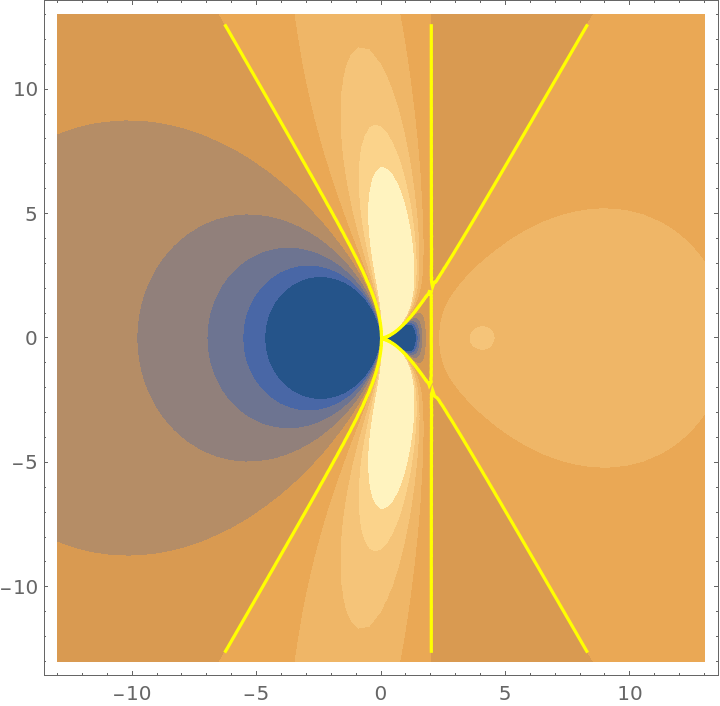
Plot the cissoid (orange) and intrinsic curvature (yellow); the background is for values other than zero:

In[5]:=
With[{a = -2}, Show[ContourPlot[imp, {x, -13, 13}, {y, -13, 13}, Contours -> 10, MaxRecursion -> 3, ContourStyle -> None, ClippingStyle -> Automatic], ContourPlot[imp == 0, {x, -4 Pi, 4 Pi}, {y, -4 Pi, 4 Pi}, PlotPoints -> 50, ContourStyle -> Yellow], ContourPlot[cissoid == 0, {x, -4 Pi, 4 Pi}, {y, -4 Pi, 4 Pi}, ContourStyle -> Orange]]]
Out[5]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 21 July 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information