Function Repository Resource:

HyperbolaProperties

Get an Association of the properties of a given hyperbola

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["HyperbolaProperties"][expr,{x,y}]

returns an Association of properties of the hyperbola defined by expr in terms of the variables x and y.

Details and Options

The input expr can be an equation or an Association of hyperbola properties. In this case, ResourceFunction["HyperbolaProperties"] will calculate and return the full set of properties.

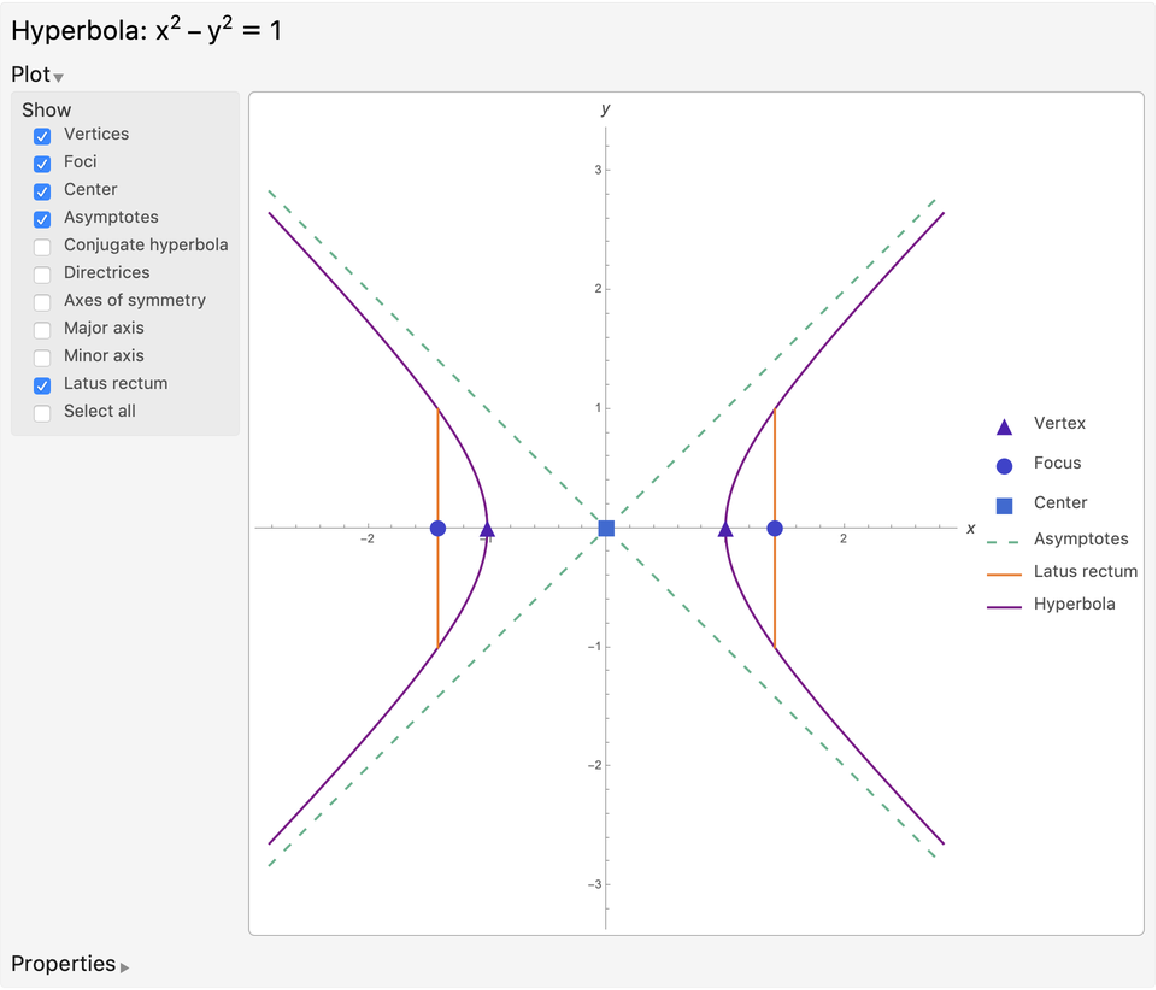
Hyperbola properties include "Equation", "Foci", "Vertices", "Eccentricity", "Asymptotes", "Center", "SemimajorAxisLength", "SemiminorAxisLength", "Directrices", "AxesOfSymmetry", "SemiLatusRectum", "RotationAngle", "ConjugateHyperbola" and "BaseConic".

The "BaseConic" property is an association of the properties "Equation", "RotationAngle" and "DisplacementFromOrigin", where "Equation" represents an isomorphic conic section based at the origin and aligned with the x-axis.

If the given expr describes a conic section other than an hyperbola, ResourceFunction["HyperbolaProperties"] will issue a message and return an Association of properties pertaining to the correct conic section.

Examples

Basic Examples (1)

Compute the properties of a hyperbola:

In[1]:=

$ResourceFunction["HyperbolaProperties"][x^2 - y^2 == 1, {x, y}]$

Out[1]=

Scope (3)

Compute the properties of a hyperbola described using other properties:

In[2]:=

Out[2]=

Compute the properties of a skew hyperbola (not aligned with the x- or y-axis) described by some properties:

In[3]:=

Out[3]=

Compute the properties of a general hyperbola centered at {h,k} with semi-axis lengths a and b:

In[4]:=

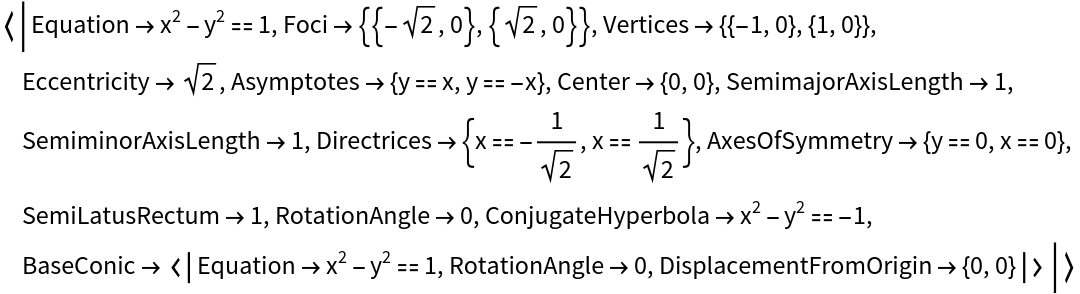
$Assuming[a > 0 && b > 0, ResourceFunction[ "HyperbolaProperties"][(x - h)^2/a^2 - (y - k)^2/b^2 == 1, {x, y}, "ReturnType" -> True]]$

Out[4]=

Properties and Relations (1)

Use the resource function InteractiveConicPlot to visualize the results of HyperbolaProperties:

In[5]:=

$ResourceFunction["InteractiveConicPlot"][x^2 - y^2 == 1, {x, y}]$

Out[5]=

Possible Issues (1)

If the input equation or Association does not describe a hyperbola but describes another conic section, HyperbolaProperties will return an Association of properties pertaining to the correct conic section, including its "Type" ("Parabola", "Circle" or "Ellipse"):

In[6]:=