Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 HurwitzMatrix (1.0.0) current version: 1.1.0 »

Source Notebook

Generate the Hurwitz matrix of a univariate polynomial

Contributed by: Jan Mangaldan

ResourceFunction["HurwitzMatrix"][poly,x]

gives the Hurwitz matrix of poly, treated as a polynomial in x.

Details

The Hurwitz matrix is also called the Routh-Hurwitz matrix.
The Hurwitz matrix is a matrix constructed from the coefficients of a polynomial, and can be used to check if the polynomial's roots all have negative real parts.
In control theory, a polynomial is stable if all of its roots have negative real parts. One can use principal minors of the Hurwitz matrix to make this determination.

Examples

Basic Examples (1) 

Generate the Hurwitz matrix of a polynomial:

In[1]:=
ResourceFunction["HurwitzMatrix"][5 + 4 x + 3 x^2 + 2 x^3 + x^4 + x^5, x] // MatrixForm
Out[1]=

Scope (2) 

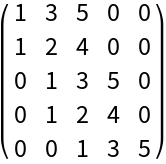Generate the Hurwitz matrix from a polynomial with numeric coefficients:

In[2]:=
ResourceFunction["HurwitzMatrix"][2 x^6 - 5 x^5 - 3 x + 9, x] // MatrixForm
Out[2]=

Generate the Hurwitz matrix from a polynomial with symbolic coefficients:

In[3]:=
ResourceFunction["HurwitzMatrix"][\!\( \*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(7\)]\(\* TemplateBox[{"k"}, "C"] \*SuperscriptBox[\(x\), \(k\)]\)\), x] // MatrixForm
Out[3]=

Applications (2) 

Use HurwitzMatrix to check the stability of a polynomial:

In[4]:=
poly = 1 + x/2 + x^2/9 + x^3/72 + x^4/1008 + x^5/30240; MatrixForm[ma = ResourceFunction["HurwitzMatrix"][poly, x]]
Out[4]=
In[5]:=
Table[Det[Take[ma, k, k]] > 0, {k, Exponent[poly, x]}]
Out[5]=

Verify stability by computing the roots of the polynomial:

In[6]:=
Re[x] < 0 /. NSolve[poly == 0, x]
Out[6]=

Version History

  • 1.1.0 – 27 March 2023
  • 1.0.0 – 03 March 2021

Related Resources

License Information