Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the list of lists whose entries are the hook lengths of the entries of a Young tableau
ResourceFunction["HookLengths"][p] gives a list of lists of lengths p for a partition p where an entry is the hook length of the corresponding cell in the Young tableau of p. |
The hook lengths of the integer partition (3,2,1,1):
| In[1]:= |
| Out[1]= |
Visualize the corresponding Ferrers diagram:
| In[2]:= |
| Out[2]= |
Here is a partition:
| In[3]:= |
The Young diagram with shape p:
| In[4]:= |
| Out[4]= |
A hook of length 5:
| In[5]:= |
| Out[5]= | 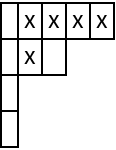 |
The hook lengths of p:
| In[6]:= |
| Out[6]= | 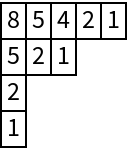 |
Here is a partition:
| In[7]:= |
The number of standard Young tableaux for the diagram of shape p (the hook length formula):
| In[8]:= |
| Out[8]= |
This is the same as the result of the resource function NumberOfTableaux:
| In[9]:= |
| Out[9]= |
This work is licensed under a Creative Commons Attribution 4.0 International License