Function Repository Resource:

HexagrammumMysticum

Source Notebook

Compute the Hexagrammum Mysticum for six points on a conic section

Contributed by: Ed Pegg Jr

ResourceFunction["HexagrammumMysticum"][{b,l,a,i,s,e}]

computes the Hexagrammum Mysticum on the conic section points {b,l,a,i,s,e}.

ResourceFunction["HexagrammumMysticum"][{b,l,a,i,s,e},"property"]

gives the specified property.

Details

ResourceFunction["HexagrammumMysticum"] returns an Association with six parts, consisting of three sets of lines (Pascal, Cayley, Pluecker) and three sets of points (Kirkman, Steiner, Salmon):

"Pascal"

Pascal lines

"Cayley"

Cayley lines

"Pluecker"

Plücker lines

"Kirkman"

Kirkman points

"Steiner"

Steiner points

"Salmon"

Salmon points

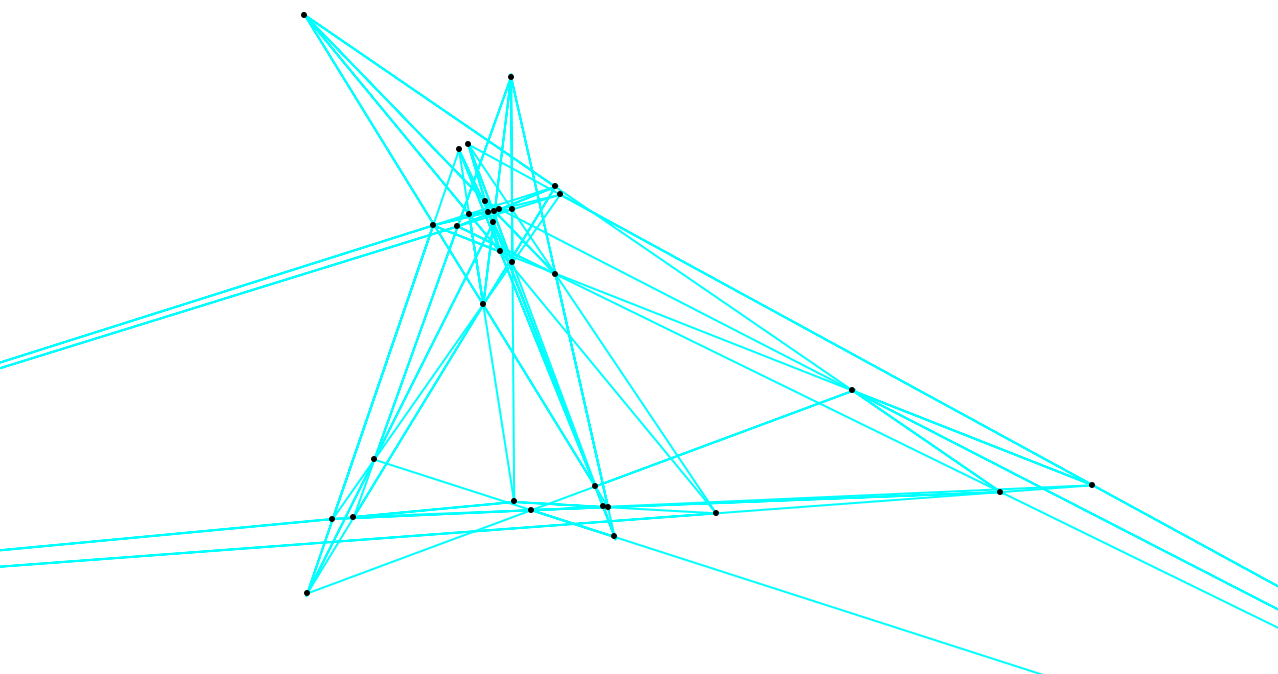
From six points on a conic section (circle, ellipse, parabola or hyperbola), label them B L A I S E and connect them to form a hexagon. There are 15 ways to choose two points, leading to 15 lines that intersect at 45 points.

If opposing sides (BL-IS, LA-SE, AI-EB) are extended, the three intersections are collinear, forming what is called a Pascal line. Six points give 60 possible hexagons, with a Pascal line for each hexagon. L(BLAISE) is one of these 60 Pascal lines.

Consider the vertices of a hexagon as a cyclic permutation and square that as a permutation. For example, BLAISE, BLSEAI and BISLAE have permutations (123456), (125634) and (145236), all with the same permutation square BAS.LIE or (135)(246). There are 20 possible results in sets of three, always giving a pair of 3-cycles. In any of these sets, the three corresponding Kirkman points are collinear, forming what is called a Cayley line. L(BAS.LIE) is one of these 20 Cayley lines.

Consider one of the 15 triplets of 2-cycles, such as BL.AI.SE or (12)(34)(56). Find the four Steiner points that commute with the given cycle under permutation products. In this case, (12)(34)(56)×(135)(246)=(135)(246)×(12)(34)(56), and similarly for (136)(245), (145)(236) and (146)(235). These four Steiner points are collinear, forming what is called the Plücker line. L(BL.AI.SE) is one of these 15 Plücker lines.

For a given hexagon on six points, consider the three other hexagons that share no edges with the first. For the hexagon BLAISE, the three others are BASLEI, BAEILS and BILEAS. These three hexagons define three Pascal lines that concur on a Kirkman point. Each of the 60 hexagons defines a Kirkman point. P(BLAISE) is one of these 60 Kirkman points.

Just as in Cayley's case, consider a hexagon as a cyclic permutation and square that as a permutation. There are 20 possible results in sets of three. In any of these sets, the three corresponding Pascal lines concur on a Steiner point. P(BAS.LIE) is one of these 20 Steiner points.

As shown in Plücker, consider one of the 15 triplets of 2-cycles. The four corresponding Cayley lines concur on a Salmon point. P(BL.AI.SE) is one of these 15 Salmon points.

There are 60 Pascal lines and 60 Kirkman points, 20 Cayley lines and 20 Steiner points, and 15 Plücker lines and 15 Salmon points, for a total of 95 lines and 95 points that form what is called the Hexagrammum Mysticum.

Conway extended Hexagrammum Mysticum even more, but that's an exercise for the user.

Sets of six small integer points on a conic which avoid parallelization problems are difficult to find. A short list of examples is provided in the Definition section.

Examples

Basic Examples (5)

Compute the Hexagrammum Mysticum for a set of six points on a conic:

In[1]:=

pts = {{-12, -3}, {3, -6}, {3, 7}, {9, -3}, {11, -1}, {12, 1}};
hm = ResourceFunction["HexagrammumMysticum"][pts];
Style[Short /@ hm, 8]

Out[3]=

Show the fifteen Salmon points:

In[4]:=

Out[4]=

Show the Values of the 15 Plücker lines in the HessianLine form:

In[5]:=

Out[5]=

Check that the six points are on the same conic:

In[6]:=

Out[6]=

Along with the original six points, show the 20 Cayley lines in green and the 15 Plücker lines in red:

In[7]:=

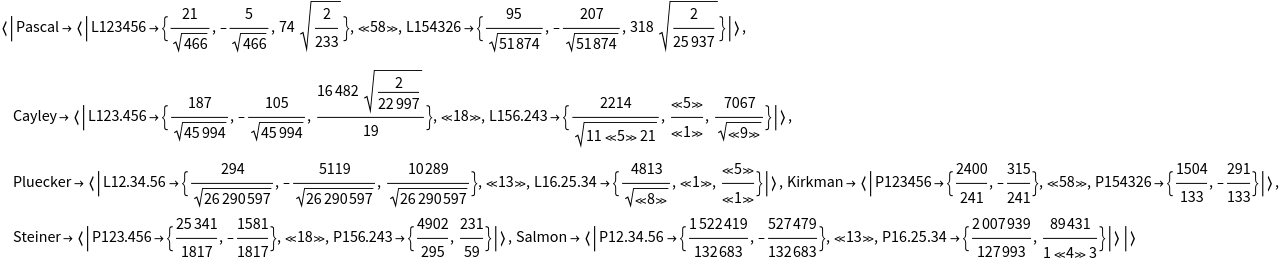
$Graphics[{AbsoluteThickness[.2], Green, Hyperplane[Take[#, 2], Last[#]] & /@ (Values@Lookup[hm, "Cayley"]), Red, Hyperplane[Take[#, 2], Last[#]] & /@ (Values@ Lookup[hm, "Pluecker"]), ContourPlot[-135 + \[FormalX]^2 - \[FormalX] \[FormalY] + 3 \[FormalY]^2 == 0, {\[FormalX], -13, 21}, {\[FormalY], -8, 8}][[1]], Black, Point[pts]}, PlotRange -> {{-13, 21}, {-8, 8}}]$

Out[7]=

Scope (2)

Get the first Pascal line for a set of six points on a conic in HessianLine form:

In[8]:=

Out[9]=

Verify that lines drawn through sequentially ordered points have three intersections concurrent with the Pascal line:

In[10]:=

Graphics[{AbsoluteThickness[1],
Cyan, InfiniteLine[#] & /@ Partition[points, 2, 1, 1],
Red, Hyperplane[Take[pascal1, 2], Last[pascal1]],
Black, ResourceFunction["NumberedPointPlot"][points][[1]]},
PlotRange -> {{-16, 20}, {-20, 15}}]

Out[10]=

Compute the Pascal lines and Kirkman points for a set of six points on a conic:

In[11]:=

For the sixty Kirkman points, we first need the canonical hexagons, since each hexagon has group D₆=12 orderings that are equivalent, such as {1,2,3,4,5,6} and {2,3,4,5,6,1}:

In[12]:=

Out[13]=

Find the three hexagons that don't share an edge with a given hexagon:

In[14]:=

Out[14]=

Use that to identify three Pascal lines:

In[15]:=

Out[15]=

Pull those lines out of the Hexagrammum Mysticum:

In[16]:=

Out[16]=

Next, obtain the particular Kirkman point:

In[17]:=

Out[17]=

Put a blue circle around the Kirkman point where three red Pascal lines intersect:

In[18]:=

Graphics[{AbsoluteThickness[1],
Table[{{Purple, Yellow, Cyan}[[k]], InfiniteLine[#] & /@ (Partition[points[[kirkhex[[k]]]], 2, 1, 1])}, {k, 1, 3}],
Red, Hyperplane[Take[#, 2], Last[#]] & /@ lines,
Black, ResourceFunction["NumberedPointPlot"][points][[1]],
Blue, Circle[kp, 1/4]},
PlotRange -> {{-16, 20}, {-20, 15}}]

Out[18]=

Possible Issues (2)

Generate a random set of six points on a conic:

In[19]:=

$ran = RandomReal[{-4, 4}, {5, 2}]; conic = ResourceFunction["FivePointConic"][ran]; randomconic6 = Append[ran, {0, Sort[\[FormalY] /. (Quiet@Solve[{\[FormalX] == 0, conic == 0}])][[ 1]]}]$

Out[21]=

The chance of parallel lines from random points is virtually zero, so the calculations will usually work:

In[22]:=

Out[22]=

(Not shown) A simple lattice point hexagon with parallel sides will generate points at infinity, so the 95 points and 95 lines won't actually exist. This generates a lot of errors, currently.