Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a skew graph on a torus with a given number of hexagonal cells
ResourceFunction["HexagonalTorusGraph"][hexagons,{a,b}] makes an (a,b)-skew torus graph with a given number of hexagons. |
There is a unique hexagonal torus graph with eight cells:
| In[1]:= |
| Out[1]= | 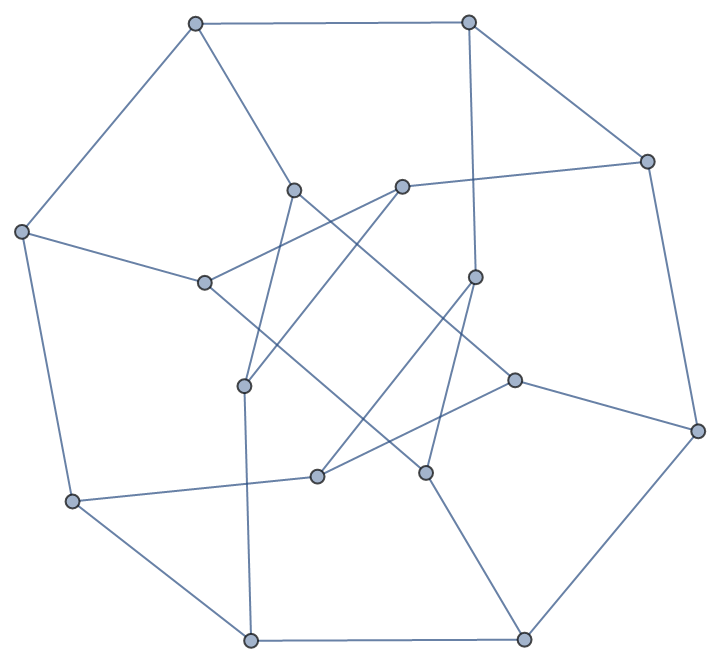 |
A 30-hexagon toroidal graph in 3D:
| In[2]:= |
| Out[2]= | 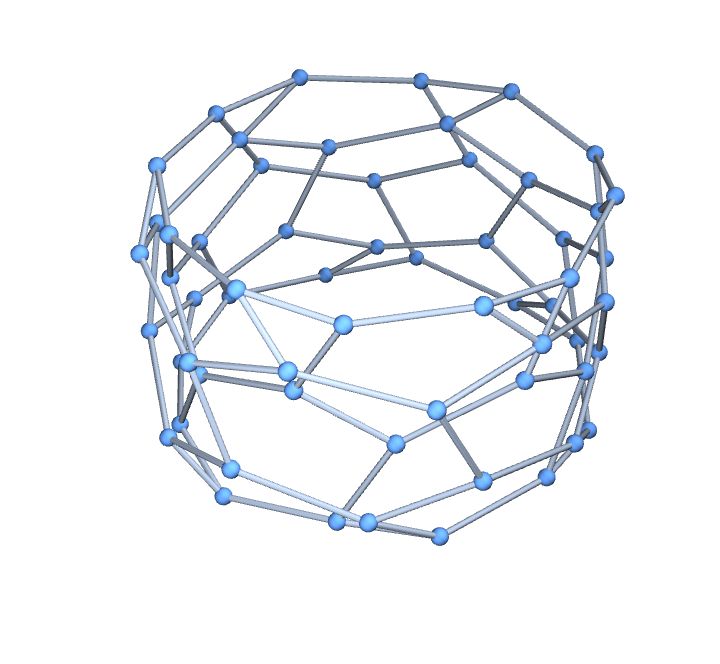 |
When a hexagonal torus graph of this form exists, the toroidal dual is the circulant graph (a, b, a+b):
| In[3]:= |
| Out[3]= | 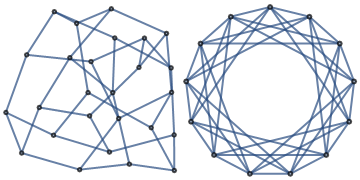 |
Some skew values are invalid:
| In[4]:= |
| Out[4]= |
The torus graphs corresponding to the toroidal duals of the following sextic toroidal graphs up to 20 vertices are out of scope for this function:
| In[5]:= |
The number of distinct torus graphs with 7 to 100 hexagons is given by the following code (see A129033):
| In[6]:= | ![T2[n_] := Piecewise[{{DivisorSigma[0, n] - 2 - T6[n], Mod[n, 2] == 1}, {DivisorSigma[0, n/2] - 2, Mod[n, 4] == 2}}, DivisorSigma[0, n/2] + DivisorSigma[0, n/4] - 4 - T6[n]];
T3[n_] := Length[{ToRules[
Reduce[n == p^2 + p q + q^2 && 0 < q < p, {p, q}, Integers]]}];
T6[n_] := Boole[n >= 9 && (IntegerQ[Sqrt[n]] || IntegerQ[Sqrt[n/3]])]
T[n_] := Piecewise[{{DivisorSigma[1, n]/6 + T2[n]/2 + 2/3 T3[n] + 5/6 T6[n] - (2 - Mod[n, 2]), n > 6}}];
Table[T[n], {n, 7, 100}]](https://www.wolframcloud.com/obj/resourcesystem/images/e4d/e4df3ae1-e784-43de-bdd7-6e75ce4c909a/6063659be4bfb336.png) |
| Out[6]= |  |
The 33 distinct hexagonal torus graphs up to 20 hexagons that can be made with this method:
| In[7]:= | ![distinctgraphs = {{7, {1, 2}}, {8, {1, 2}}, {9, {1, 2}}, {10, {1, 3}}, {11, {1, 2}}, {12, {1, 2}}, {12, {1, 3}}, {12, {1, 4}}, {13, {1, 2}}, {13, {1, 3}}, {14, {1, 2}}, {14, {1, 3}}, {15, {1, 2}}, {15, {1, 3}}, {15, {1, 4}}, {15, {2, 3}}, {16, {1, 2}}, {16, {1, 3}}, {16, {2, 3}}, {17, {1, 2}}, {17, {1, 3}}, {18, {1, 2}}, {18, {1, 3}}, {18, {1, 4}}, {18, {1, 5}}, {19, {1, 2}}, {19, {1, 3}}, {19, {2, 3}}, {20, {1, 2}}, {20, {1, 3}}, {20, {1, 4}}, {20, {2, 3}}, {20, {3, 4}}};
Column[Row /@ Partition[
ResourceFunction["HexagonalTorusGraph"] @@ # & /@ distinctgraphs, UpTo[5]]]](https://www.wolframcloud.com/obj/resourcesystem/images/e4d/e4df3ae1-e784-43de-bdd7-6e75ce4c909a/10cdba88a26ff151.png) |
| Out[7]= | 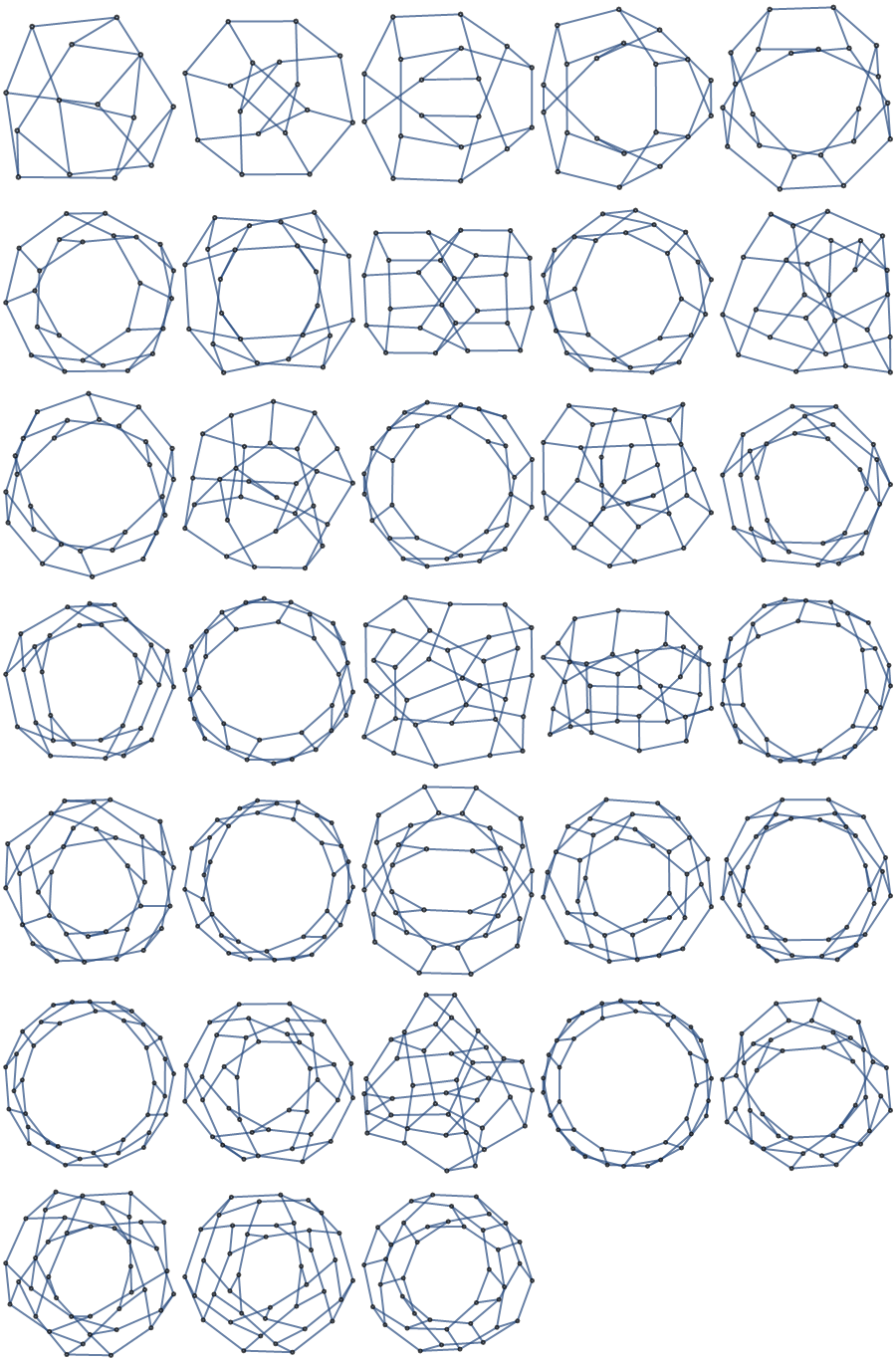 |
This work is licensed under a Creative Commons Attribution 4.0 International License