Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 HexagonalSpiralPoints

Source Notebook

Get the coordinates of the points on a hexagonal spiral

Contributed by: George Beck

ResourceFunction["HexagonalSpiralPoints"][n]

gives the list of coordinate pairs on a hexagonal spiral with n sides starting with the origin.

Details and Options

The list starts at the origin and roughly goes NE, NW, W, SW, SE, E and repeats.

Examples

Basic Examples (4) 

Here are the points on the first four legs of the spiral:

In[1]:=
ResourceFunction["HexagonalSpiralPoints"][4]
Out[1]=

This shows the sequence of points in order for six sides:

In[2]:=
With[{s = ResourceFunction["HexagonalSpiralPoints"][6]}, Graphics[{{Pink, PointSize[.03], Point[s]}, Arrow@Partition[s, 2, 1]}]]
Out[2]=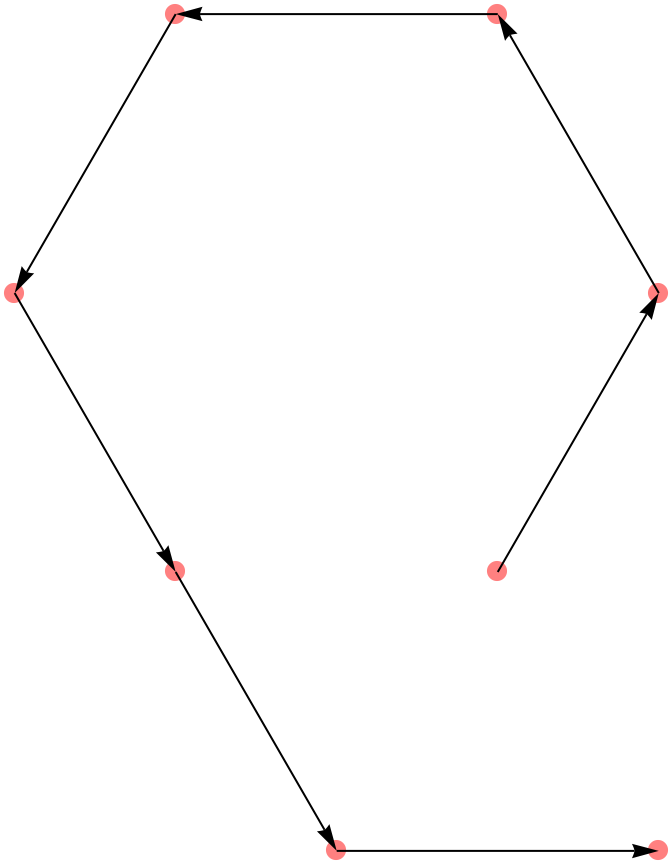

40 black sides with 20 red sides overlaid:

In[3]:=
Graphics[{Line@ResourceFunction["HexagonalSpiralPoints"][40], Red, Line@ResourceFunction["HexagonalSpiralPoints"][20]}]
Out[3]=

The number of points in the first n sides:

In[4]:=
Length@ResourceFunction["HexagonalSpiralPoints"]@# & /@ Range[0, 20]
Out[4]=
In[5]:=
Table[Round[(n + 3)^2/12], {n, 21}]
Out[5]=

Neat Examples (2) 

This finds the coordinate pairs that are a prime distance counting along the square spiral:

In[6]:=
UlamHexagonalSpiralPoints[n_] := ResourceFunction["HexagonalSpiralPoints"][n][[ Select[Range[Round[(n + 4)^2/12]], PrimeQ] ]]

The larger points correspond to the primes 2, 3, 5, 7, 11, 13:

In[7]:=
With[{n = 9}, Graphics[{{LightGray, Line@ResourceFunction["HexagonalSpiralPoints"]@n}, Point@ResourceFunction["HexagonalSpiralPoints"]@n, PointSize[.08], Point@UlamHexagonalSpiralPoints@n}, ImageSize -> 100]]
Out[7]=

About 12% of the numbers up to 10443 are prime:

In[8]:=
With[{n = 350}, Round[(n + 4)^2/12]]
Out[8]=
In[9]:=
PrimePi@%
Out[9]=

Here is a plot of the first 1277 primes:

In[10]:=
Graphics@Point@UlamHexagonalSpiralPoints@350
Out[10]=

About 11% of the numbers to 10443 are lucky:

In[11]:=
ResourceFunction["LuckyNumbers"]@10443 // Length
Out[11]=

This finds the coordinate pairs that are at lucky number distances along the hexagonal spiral:

In[12]:=
LuckyHexagonalSpiralPoints[n_] := ResourceFunction["HexagonalSpiralPoints"][n][[ ResourceFunction["LuckyNumbers"][Round[(n + 4)^2/12]] ]]

Here are the first 1248 lucky numbers plotted along the hexagonal spiral:

In[13]:=
Graphics@Point@LuckyHexagonalSpiralPoints@350
Out[13]=

Publisher

George Beck

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 26 February 2019

Related Resources

License Information