Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the Hessian normal form of a plane passing through three given points in space
ResourceFunction["HessianPlane"][pts] returns the Hessian plane for pts. |
Find the Hessian plane through three points:
| In[1]:= |
| Out[1]= |
The first three components form a unit vector:
| In[2]:= |
| Out[2]= |
Show the plane, points and normal vector:
| In[3]:= | ![Graphics3D[{Sphere[pts, Scaled[0.02]],
{Directive[Black, Arrowheads[Medium]], Arrow[Tube[{Mean[pts], Mean[pts] - 1.5 Most[hp]}]]},
{Directive[Opacity[0.5], ColorData[97, 2]], Hyperplane[Most[hp], -Last[hp]]}}, {ImageSize -> Small, PlotRange -> {{-2, 1}, {-2, 1}, {-2, 1}}, PlotRangePadding -> Scaled[0.05]}]](https://www.wolframcloud.com/obj/resourcesystem/images/750/750c950a-f0a9-42df-b671-49b1bc3f5a04/2a8e0cb43ad989b6.png) |
| Out[3]= |  |
Timing can be faster than RegionDistance in some cases (though usually it is not):
| In[4]:= |
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= |
HessianPlane fails if the given points do not determine a plane:
| In[8]:= |
| Out[8]= |
Points of a random tetrahedron centered at the origin:
| In[9]:= |
| Out[9]= |
Face planes of the tetrahedron:
| In[10]:= |
| Out[10]= | 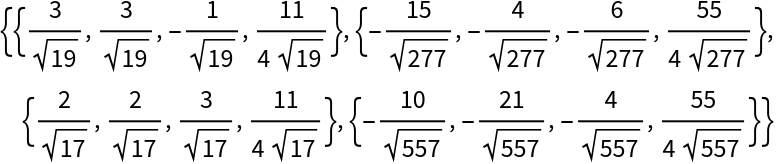 |
Incenters of each face, using the resource function Incircle3D:
| In[11]:= |
Perpendiculars to the incenters do not not intersect, therefore this tetrahedron does not have a midsphere tangent to all edges:
| In[12]:= | ![Graphics3D[{{EdgeForm[Gray], Opacity[0.5], Tetrahedron[v]},
{Black, Composition[Tube[#, Scaled[0.002]] &, ResourceFunction["Incircle3D"]] /@ Subsets[v, {3}]},
Table[Tube[{in[[k]], in[[k]] + Most[fp[[k]]]}, 0.06], {k, 4}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/750/750c950a-f0a9-42df-b671-49b1bc3f5a04/09e5d1d970a66751.png) |
| Out[12]= | 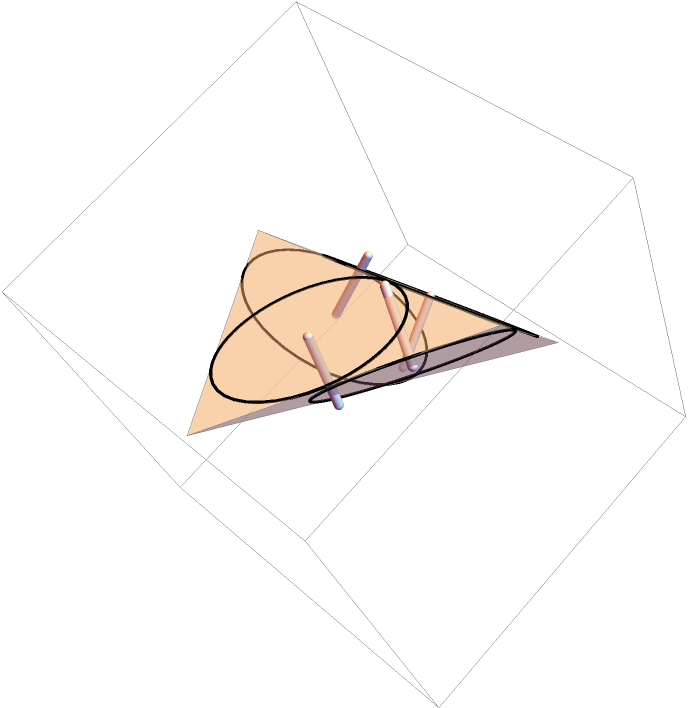 |
This work is licensed under a Creative Commons Attribution 4.0 International License