Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Convert integer tuples into Heegner field primes when applicable
ResourceFunction["HeegnerPrime"][{a,b},h] converts tuple {a,b} into a prime number for field |
Show the Heegner primes generated by tuple {1,2}:
| In[1]:= |
|
| Out[1]= |
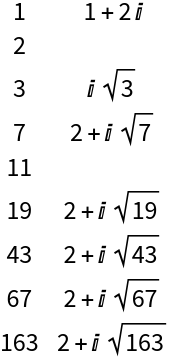
|
Tuples with a common divisor do not have corresponding Heegner primes:
| In[2]:= |
|
| Out[2]= |
|
Applying HeegnerPrime to these tuples gives Null:
| In[3]:= |
|
| Out[3]= |
|
Generate some Eisenstein primes from the field ![]() :
:
| In[4]:= |
![eisenstein = Select[ResourceFunction["HeegnerPrime"][#, 3] & /@ Tuples[Range[-19, 19], {2}], Norm[#] <= Sqrt[317] &];
Short[eisenstein]](https://www.wolframcloud.com/obj/resourcesystem/images/55b/55b237ac-fb25-4fe6-a1fe-29950a2bcf6d/3bca97c690c801dc.png)
|
| Out[5]= |
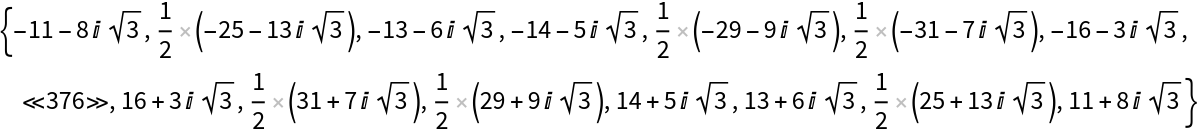
|
Show these in the complex plane:
| In[6]:= |
|
| Out[6]= |

|
The tuple {19,30} generates all Heegner primes, except the corresponding Gaussian prime:
| In[7]:= |
|
| Out[7]= |
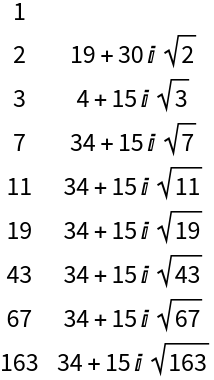
|
Generate some Gaussian primes from the field ![]() :
:
| In[8]:= |
![gaussian = Select[ResourceFunction["HeegnerPrime"][#, 1] & /@ Tuples[Range[-30, 30], {2}], Norm[#] <= Sqrt[700] &];
Short[gaussian]](https://www.wolframcloud.com/obj/resourcesystem/images/55b/55b237ac-fb25-4fe6-a1fe-29950a2bcf6d/0fedabf147497482.png)
|
| Out[9]= |
|
Show these in the complex plane:
| In[10]:= |
|
| Out[10]= |

|
Show some Kleinian primes from the field ![]() :
:
| In[11]:= |
![kleinian = Select[ResourceFunction["HeegnerPrime"][#, 7] & /@ Tuples[Range[-23, 23], {2}], Norm[#] <= Sqrt[540] &];
Graphics[Disk[ReIm[#], .5] & /@ kleinian]](https://www.wolframcloud.com/obj/resourcesystem/images/55b/55b237ac-fb25-4fe6-a1fe-29950a2bcf6d/382cfbe0958c6f26.png)
|
| Out[11]= |

|
This work is licensed under a Creative Commons Attribution 4.0 International License