Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 HarshadNumberQ

Source Notebook

Test if a number is a harshad number

Contributed by: Sander Huisman

ResourceFunction["HarshadNumberQ"][n]

gives True if n is a harshad number and False otherwise.

ResourceFunction["HarshadNumberQ"][n,b]

gives True if n is a b-harshad number and False otherwise.

Details

A harshad number is also called a Niven number.
A b-harshad number is a number divisible by the sum of its digits in base b. A harshad number is a 10-harshad number.
For negative n or b, the sign is ignored.
ResourceFunction["HarshadNumberQ"] threads over lists.

Examples

Basic Examples (2) 

Test if 2023 is a harshad number:

In[1]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][2023]
Out[1]=

Test another number:

In[2]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][2026]
Out[2]=

Scope (2) 

Test a list of numbers:

In[3]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Range[2000, 2030]]
Out[3]=

Give the base explicitly:

In[4]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][2026, 10]
Out[4]=

Use a different base:

In[5]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][2026, 45]
Out[5]=

Possible Issues (3) 

Base 0 cannot be computed:

In[6]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][2026, 0]
Out[6]=

Base 1 cannot be computed:

In[7]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][2026, 1]
Out[7]=

The number 0 cannot be divided by itself:

In[8]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][0]
Out[8]=

Neat Examples (5) 

12 is a harshad number in multiple bases:

In[9]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][12, {2, 3, 4, 5, 7, 11, 16, 32}]
Out[9]=

12 is not an 8-harshad number:

In[10]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][12, 8]
Out[10]=

The number 2016502858579884466176 is a multiple harshad number:

In[11]:=
NestWhileList[ Quotient[#, Total[IntegerDigits[#]]] &, 2016502858579884466176, ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][#] && # > 1 &, 1, \[Infinity], -1]
Out[11]=
In[12]:=
ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][%]
Out[12]=

Find the first 1000 harshad numbers and visualize them:

In[13]:=
numbers = ResourceFunction["FindFirstNumberInstance"][ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], {1, \[Infinity]}, 1000]; ListLinePlot[numbers]
Out[14]=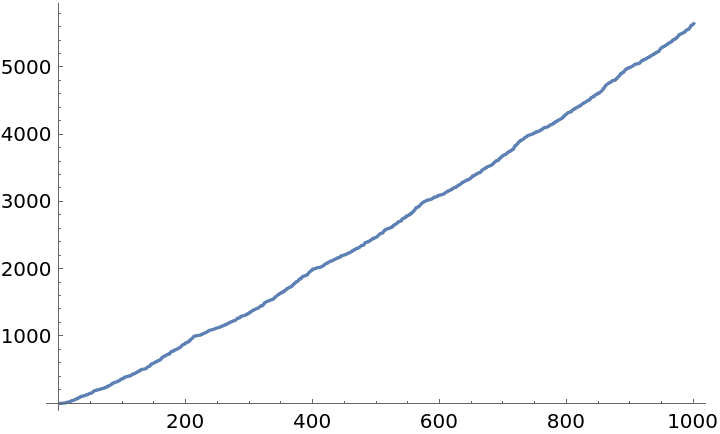

All numbers up to 10000 are either a harshad number or the sum of two harshad numbers:

In[15]:=
max = 10000; hnh = GroupBy[Range[max], ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"]]; AllTrue[hnh[False], ContainsAny[# - hnh[True], hnh[True]] &]
Out[17]=

The first factorial that is not a harshad number is 432:

In[18]:=
ResourceFunction["FindFirstNumberInstance"][ Not[ResourceFunction[ "HarshadNumberQ", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][#!]] &, \[Infinity], 1]
Out[18]=

Publisher

SHuisman

Version History

  • 1.1.0 – 22 February 2023
  • 1.0.0 – 09 January 2023

Related Resources

License Information