Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate three cyclic harmonic quadrangles from a reference triangle
ResourceFunction["HarmonicQuadrilaterals"][{p1,p2,p3}] gives the three harmonic quadrilaterals corresponding to the triangle with corner points p1,p2, and p3. |
Find three harmonic quadrilaterals that contain a triangle:
| In[1]:= |
| Out[2]= |  |
Show these:
| In[3]:= | ![GraphicsRow[Graphics[{
{Dashed, TriangleConstruct[tri, "Circumcircle"]}, {Transparent, EdgeForm[Thick], #},
{RGBColor[0, 0, 1], HatchFilling[], EdgeForm[
RGBColor[0, 0, 1]], Triangle[tri]}}
] & /@ quads] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/6c98e4b610657548.png) |
| Out[3]= | 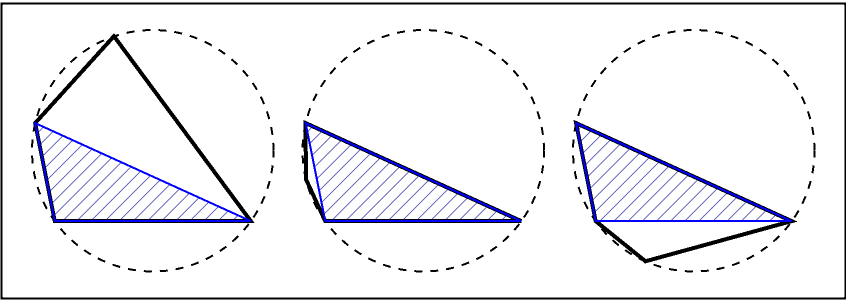 |
The products of the lengths of opposite sides are equal:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |
Some spiral similar triangles pairs (marked as red and blue) can be found by halving the diagonal or the extension of a side:
| In[6]:= |
Take the midpoint of one diagonal:
| In[7]:= | ![q = Midpoint[quad[[{1, 3}]]];
Graphics[{Sequence[{Dashed,
Line[
Part[quad, {1, 3}]]}, {Dashed,
TriangleConstruct[tri, "Circumcircle"]}, {Transparent,
EdgeForm[Thick],
Polygon[quad]}],
{RGBColor[0, 0, 1], HatchFilling[], EdgeForm[
RGBColor[0, 0, 1]], Triangle[tri]},
{RGBColor[1, 0, 0], HatchFilling[], EdgeForm[
RGBColor[1, 0, 0]], Triangle[{quad[[2]], quad[[3]], q}]}}
]](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/6e4db55a42e6f2fb.png) |
| Out[8]= | 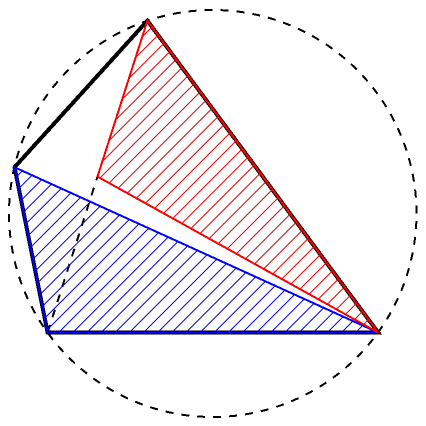 |
| In[9]:= | ![Graphics[{Sequence[{Dashed,
Line[
Part[quad, {1, 3}]]}, {Dashed,
TriangleConstruct[tri, "Circumcircle"]}, {Transparent,
EdgeForm[Thick],
Polygon[quad]}],
{RGBColor[0, 0, 1], HatchFilling[], EdgeForm[
RGBColor[0, 0, 1]], Triangle[{quad[[3]], quad[[4]], q}]},
{RGBColor[1, 0, 0], HatchFilling[], EdgeForm[
RGBColor[1, 0, 0]], Triangle[{quad[[2]], quad[[3]], q}]}}
]](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/544671f6259d80d0.png) |
| Out[9]= | 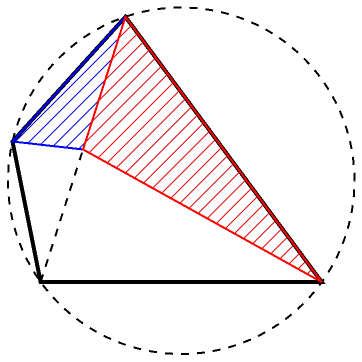 |
| In[10]:= | ![Graphics[{Sequence[{Dashed,
Line[
Part[quad, {1, 3}]]}, {Dashed,
TriangleConstruct[tri, "Circumcircle"]}, {Transparent,
EdgeForm[Thick],
Polygon[quad]}],
{RGBColor[0, 0, 1], HatchFilling[], EdgeForm[
RGBColor[0, 0, 1]], Triangle[{quad[[4]], quad[[1]], q}]},
{RGBColor[1, 0, 0], HatchFilling[], EdgeForm[
RGBColor[1, 0, 0]], Triangle[{quad[[1]], quad[[2]], q}]}}
]](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/67cb0b506bed5e36.png) |
| Out[10]= | 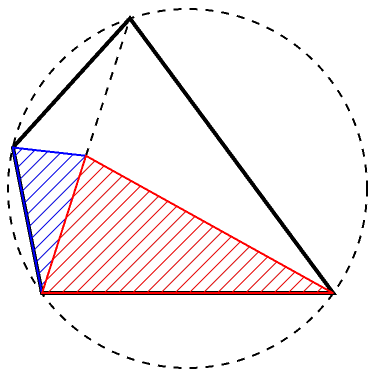 |
Double the length of one side:
| In[11]:= | ![Graphics[{
{Dashed, Line[quad[[{1, 3}]]]},
{Dashed, TriangleConstruct[tri, "Circumcircle"]},
{Transparent, EdgeForm[Thick], Polygon[quad]},
{RGBColor[0, 0, 1], HatchFilling[], EdgeForm[
RGBColor[0, 0, 1]], Triangle[tri]},
{RGBColor[1, 0, 0], HatchFilling[], EdgeForm[
RGBColor[1, 0, 0]], Triangle[{
quad[[2]], quad[[3]],
ReflectionTransform[quad[[3]] - quad[[4]], quad[[3]]][
quad[[4]]]}]}
}
]](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/55eebf2938e0fbbe.png) |
| Out[11]= | 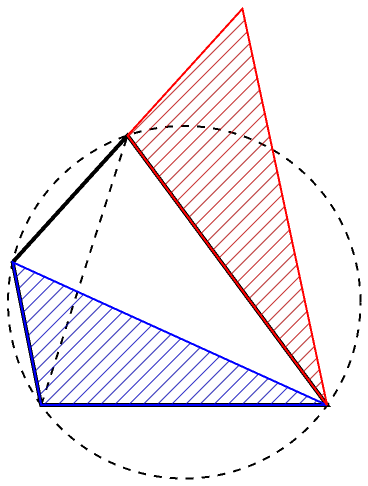 |
A harmonic quadrilateral can also be constructed with GeometricScene by equating the product of the lengths of opposite sides:
| In[12]:= | ![RandomInstance[
GeometricScene[{a, b, c, d}, {GeometricAssertion[Polygon[{a, b, c, d}], "Counterclockwise", "Cyclic"], EuclideanDistance[a, b]*EuclideanDistance[c, d] == EuclideanDistance[b, c]*EuclideanDistance[d, a]}], RandomSeeding -> 77]](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/5efd3060f84f2d61.png) |
| Out[12]= | 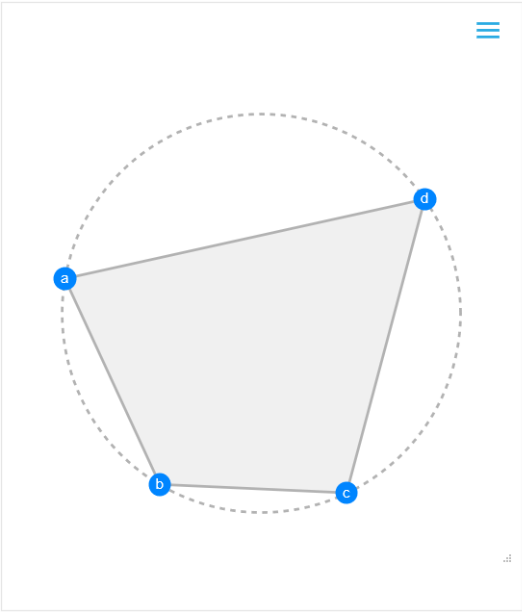 |
The vertices of a harmonic quadrilateral are inverse to some squares and vice versa. To find a proper inversion center, use the intersection of the orthogonal circles passing through the vertices of each diagonal:
| In[13]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/27102f7e-9d74-466b-9c1a-4b8be5c9590c"]](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/5cbfb1f3cf4f0f65.png) |
The intersections of the two solid orthogonal circles are the proper inversion centers:
| In[14]:= | ![Graphics[{Sequence[{Dashed,
TriangleConstruct[tri, "Circumcircle"]}, {Transparent,
EdgeForm[Thick],
Polygon[quad]}, {
RGBColor[0, 0, 1],
HatchFilling[],
EdgeForm[
RGBColor[0, 0, 1]],
Triangle[tri]}],
{Circle[twoOrthocircleCenters[[1]], twoOrthocircleradius[[1]]],
Circle[twoOrthocircleCenters[[2]], twoOrthocircleradius[[2]]]}}, PlotRange -> {{-4, 3}, {-1, 4}}
] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/088de7088fe4318a.png) |
| Out[14]= | 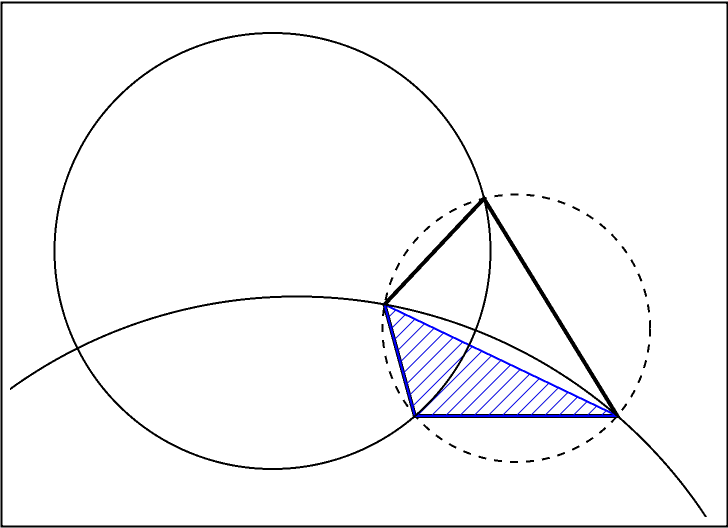 |
Either one can be chosen as the inversion center. The gray hatch-filled polygon is a square for each diagram:
| In[15]:= | ![GraphicsRow[Graphics[{
{Dashed, TriangleConstruct[tri, "Circumcircle"]},
{Transparent, EdgeForm[Thick], Polygon@quad},
{Opacity[0.6], Gray, HatchFilling[], EdgeForm[Gray], Polygon@#},
MapThread[Arrow[{#1, #2}] &, {quad, #}]
}
] & /@ invVert] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/3e25ec061e43a2a5.png) |
| Out[15]= | 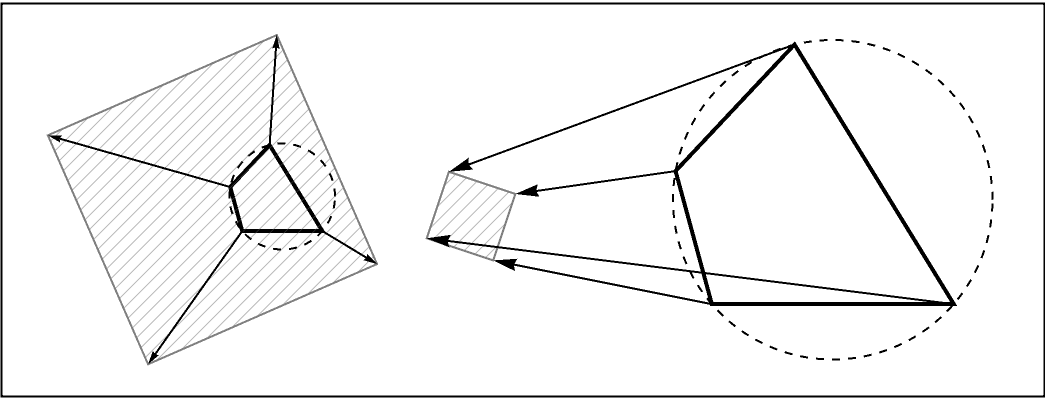 |
A weaker version of the result is that any cyclic quadrilateral (not necessary harmonic) is the inversion of some rectangle. The inversion center is found in the similar way as described above.
Generate a set of random harmonic quadrilaterals:
| In[16]:= | ![SeedRandom[11];
tri = RandomPoint[Circle[], 3];
quads = ResourceFunction["HarmonicQuadrilaterals"][tri];
GraphicsRow[Graphics[{
{Dashed, TriangleConstruct[tri, "Circumcircle"]},
{Transparent, EdgeForm[Thick], #},
{RGBColor[0, 0, 1], HatchFilling[], EdgeForm[
RGBColor[0, 0, 1]], Triangle[tri]}}
] & /@ quads] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/110b23e2f013eb5a.png) |
| Out[19]= | 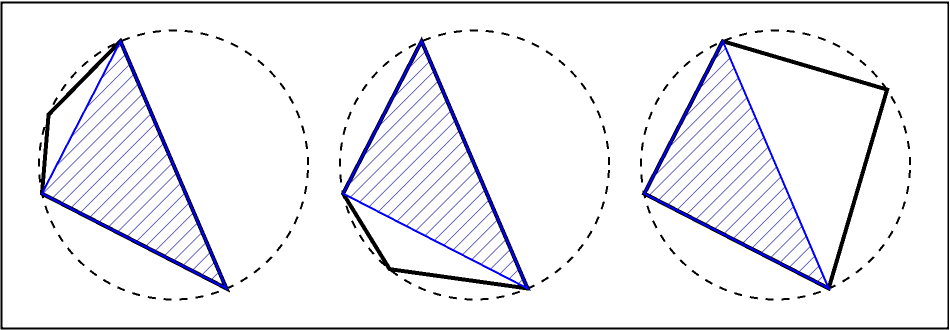 |
Check the distribution of the area of harmonic quadrilaterals in the unit circle:
| In[20]:= | ![Histogram[Area /@ (Flatten@Table[
ResourceFunction["HarmonicQuadrilaterals"][
RandomPoint[Circle[], 3]], 3000]), 50]](https://www.wolframcloud.com/obj/resourcesystem/images/83b/83b98635-6c33-416e-a4a9-83f72f266ecc/22eb36b8a9ed3b00.png) |
| Out[20]= | 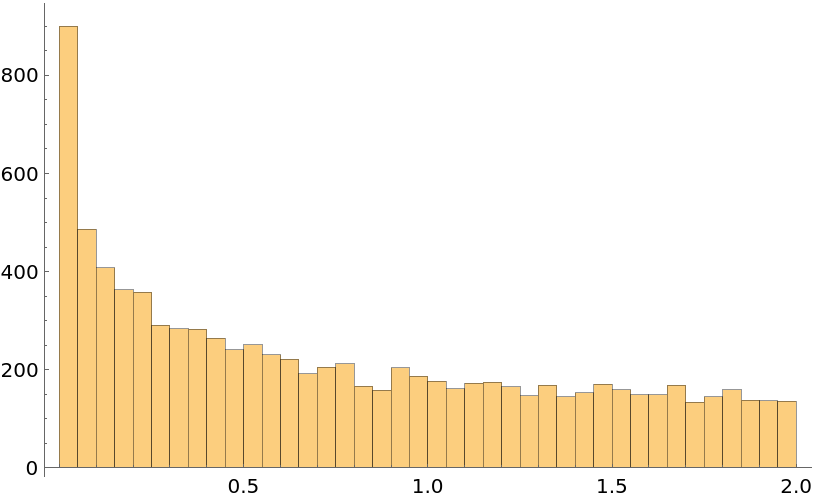 |
This work is licensed under a Creative Commons Attribution 4.0 International License