Basic Examples (2) 

Compute the half-GCD of 68 and 44:

In[1]:=

Out[1]=

Check that the half-GCD criteria are satisfied:

In[2]:=

Out[2]=

Scope (3) 

HalfGCD handles negative inputs:

In[3]:=

Out[3]=

Inputs need not be ordered by magnitude:

In[4]:=

Out[4]=

HalfGCD handles Gaussian integer inputs:

In[5]:=

Out[5]=

Check the result:

In[6]:=

Out[6]=

Properties and Relations (4) 

The half-GCD can be iterated to compute the usual GCD (a step of the Euclidean algorithm is interleaved in order to guarantee a reduction when the numbers are too far apart for HalfGCD to give a nontrivial reduction):

In[7]:=

Out[7]=

Check that 8400 is the correct GCD:

In[8]:=

Out[8]=

Check that the corresponding row of the conversion matrix gives the multipliers for the extended GCD:

In[9]:=

Out[9]=

The half-GCD is often identical (up to row signs) to the result of a certain lattice reduction:

In[10]:=

Out[11]=

In[12]:=

Out[12]=

The asymptotic speed of the half-GCD implementation is quasilinear (linear times logarithmic factors) in the size of the inputs, so doubling the sizes only slightly more than doubles the timings:

In[13]:=

Out[13]=

For large inputs (i₁,i₂), the fact that m.(i₁,i₂) gives a relatively small second element means that m₂.(i₁,i₂) can be considered approximately zero, relative to the size of inputs. This in turn implies that 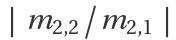is a good approximation to 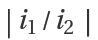. One can use this to create rational approximations of irrational values.

Find the half-GCD of the nearest integer to 10¹⁰π with the prefactor 10¹⁰:

In[14]:=

Out[14]=

Check the quotient of the second row in the multiplier matrix:

In[15]:=

Out[17]=

This quotient will often appear in the list of continued fraction approximations to π:

In[18]:=

Out[18]=

Possible Issues (1) 

When the second input divides the first and is less than the square root of the first, the GCD can be computed in one step, but HalfGCD will not take that step due to criterion (iii) noted in Details & Options:

In[19]:=

Out[19]=

Neat Examples (3) 

Thue's Lemma guarantees that for a given modulus p>1, an integer n has a rational equivalent modulo p with numerator and denominator no larger than 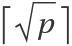. It can be found using the half-GCD. A common use case is in reconstructing rational solutions to linear equations from solutions computed over the integers modulo a power of a prime.

Code to reconstruct a rational equivalent mod p for a given n:

In[20]:=

Find the rational equivalent to 123456789 modulo the cube of the 100th prime:

In[21]:=

Out[21]=

Show that it is equivalent:

In[22]:=

Out[22]=