Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 HadamardDeviation

Source Notebook

Measure the linear-drift-insensitive, two-sample, phase/frequency stability

Contributed by: Julien Kluge

ResourceFunction["HadamardDeviation"][data,r,taus]

calculates the linear-drift insensitive two-sample deviation of data along sample times taus at rate r.

Details and Options

The Hadamard deviation is the square root of the linear-drift-insensitive two-sample variance which is used to characterize the frequency/phase stability of an oscillator.
The output usually comes in the format {τ,Around[σ,δσ]} where δσ denotes the statistical uncertainty related to the deviation σ.
The argument taus can be specified as:
{{n}}attempts to place n logarithmic spaced samples
dplaces logarithmic spaced samplings with log base d
{τ1,τ2,…}tries to use the specified sample times
Alluses all possible sample times
Automatictries to place a reasonable amount of samples along the whole possible time range
For a list of reals as a data argument, ResourceFunction["HadamardDeviation"] will use a fast, compiled algorithm. Otherwise valid inputs are exact expressions and/or Around.
The rate r must be a positive, numeric quantity.
Supported options are:
"Overlapping"Truewhether to use the overlapping Hadamard deviation
"FrequencyData"Falsespecifies whether the data argument is a list of frequencies instead of phase data

Examples

Basic Examples (3) 

Calculating the Hadamard deviation for a small sample set at a rate of 2 samples per time unit:

In[1]:=
ResourceFunction[ "HadamardDeviation"][{1.0, 2.0, 1.0, 2.1, 1.1, 1.9, 0.9, 2.2, 1.2, 1.9, 1.0, 2.1}, 2.0, Automatic]
Out[1]=

Display overlapping Hadamard deviation of white noise at a rate of 0.1 for automatically chosen sampling points:

In[2]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; hdev = ResourceFunction["HadamardDeviation"][data, 0.1, Automatic]; ListLogLogPlot[hdev, FrameLabel -> {"Averaging time \[Tau]", "Hadamard Deviation \!\(\*SubscriptBox[\(\[Sigma]\), \(y\)]\)"}, IntervalMarkersStyle -> Gray]
Out[4]=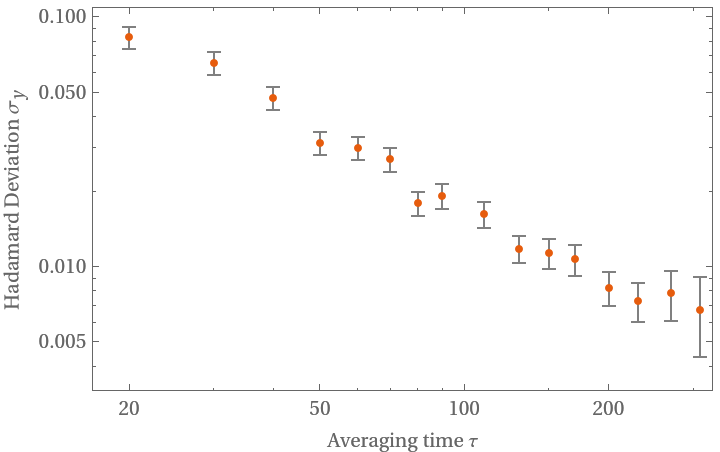

Display overlapping Hadamard deviation of white noise at a rate of 0.1 for certain sampling points:

In[5]:=
data = RandomFunction[WhiteNoiseProcess[1], {200}]["Values"]; hdev = ResourceFunction["HadamardDeviation"][data, 0.1, {20, 50, 100, 200, 400}]; ListLogLogPlot[hdev, GridLines -> Automatic]
Out[6]=

Scope (3) 

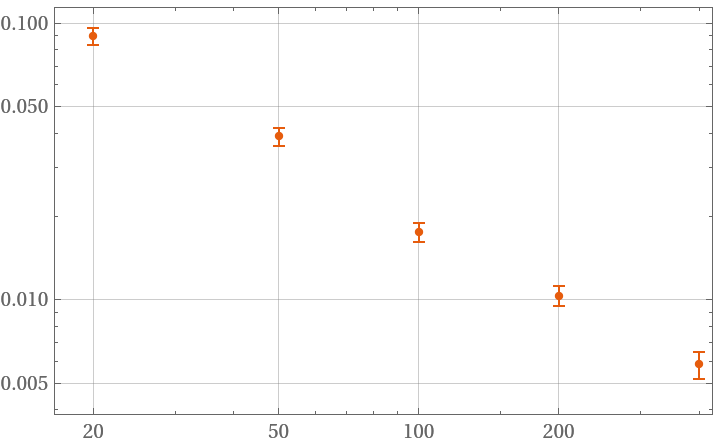Sample at all possible times:

In[7]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; hdev = ResourceFunction["HadamardDeviation"][data, 1, All]; ListLogLogPlot[hdev]
Out[8]=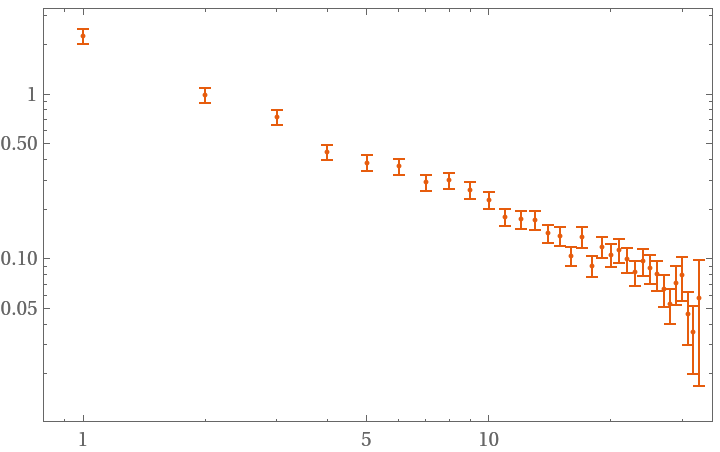

Try to sample at 4 different time values:

In[9]:=
data = RandomFunction[WhiteNoiseProcess[1], {200}]["Values"]; hdev = ResourceFunction["HadamardDeviation"][data, 1, {{4}}]; ListLogLogPlot[hdev]
Out[11]=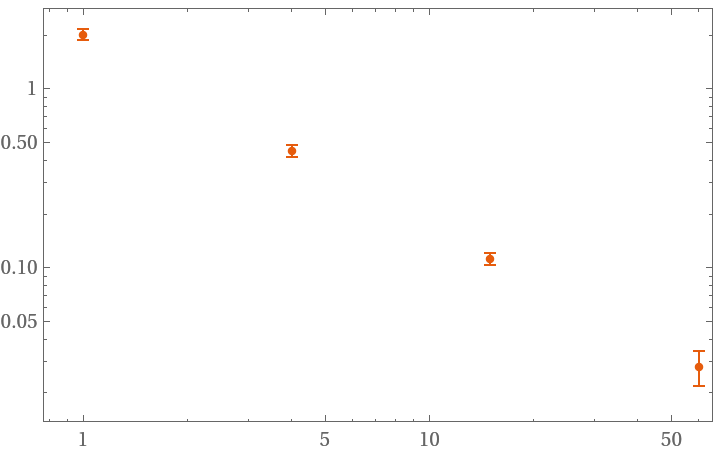

The function will try to use a fast evaluation method when the data array is fully real and otherwise prints a warning:

In[12]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; hdev = ResourceFunction["HadamardDeviation"][data~Join~{Pi}, 1, Automatic]; ListLogLogPlot[hdev]
Out[14]=

Options (2) 

FrequencyData (1) 

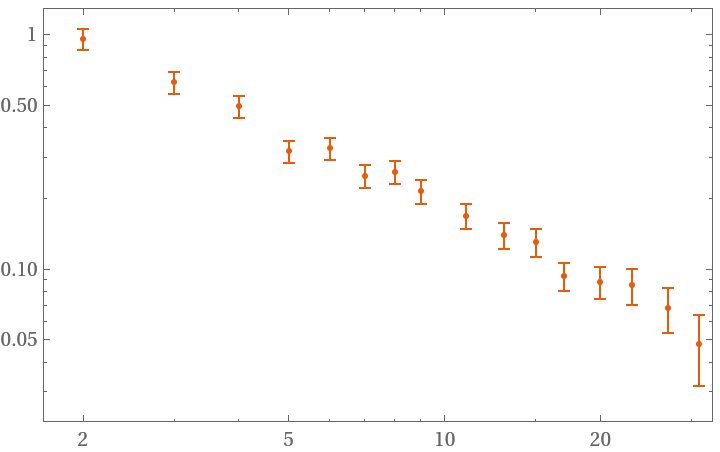FrequencyData accepts a Boolean as argument. True signals the use of frequency data as opposed to phase data:

In[15]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; hdev = ResourceFunction["HadamardDeviation"][data, 1, All, "FrequencyData" -> True]; ListLogLogPlot[hdev]
Out[17]=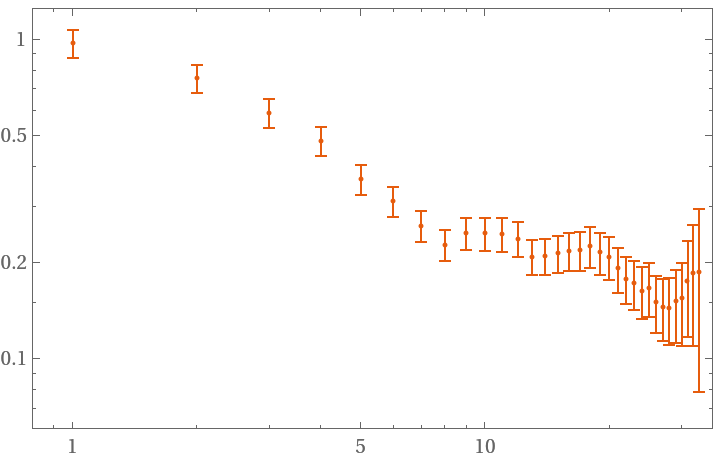

Overlapping (1) 

Overlapping accepts a Boolean as argument. False signals the use of non overlapping strides in the deviation sampling:

In[18]:=
data = RandomFunction[WhiteNoiseProcess[1], {100}]["Values"]; hdev = ResourceFunction["HadamardDeviation"][data, 1, All, "Overlapping" -> False]; ListLogLogPlot[hdev]
Out[19]=

Applications (2) 

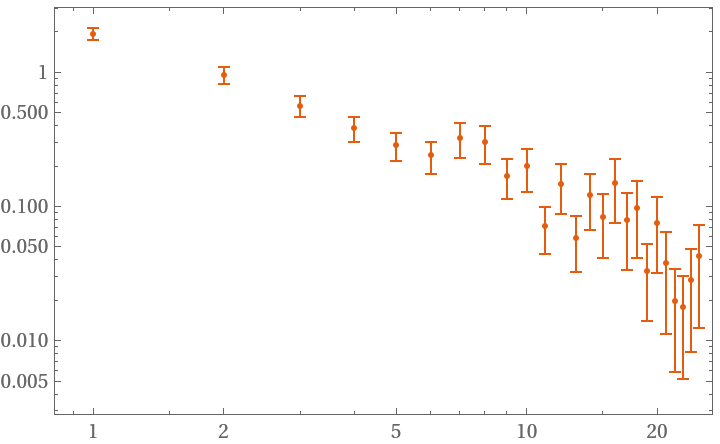Distinguish random walk from white noise by their distinct slope:

In[20]:=
datas = N[ RandomFunction[#, {10000}]["Values"]] & /@ {WhiteNoiseProcess[], RandomWalkProcess[0.5]}; hdevs = ResourceFunction["HadamardDeviation"][#, 1, Automatic] & /@ datas; ListLogLogPlot[hdevs]
Out[22]=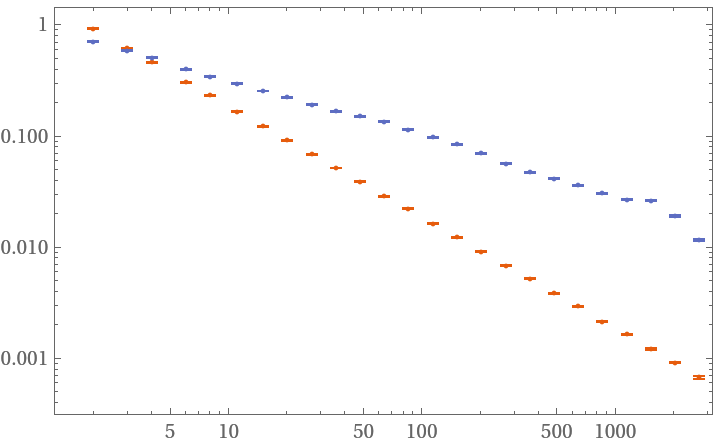

The Hadamard deviation is is approximately equal to the Allan deviation except for linear drifts:

In[23]:=
data = RandomFunction[WhiteNoiseProcess[], {10000}]["Values"] + Accumulate[ConstantArray[10^-3, 10001]]; hdev = ResourceFunction["HadamardDeviation"][data, 1.0, Automatic, "FrequencyData" -> True]; adev = ResourceFunction["AllanDeviation"][data, 1.0, Automatic, "FrequencyData" -> True]; ListLogLogPlot[{hdev, adev}, PlotLegends -> {"Hadamard deviation", "Allan deviation"}]
Out[24]=

Properties and Relations (1) 

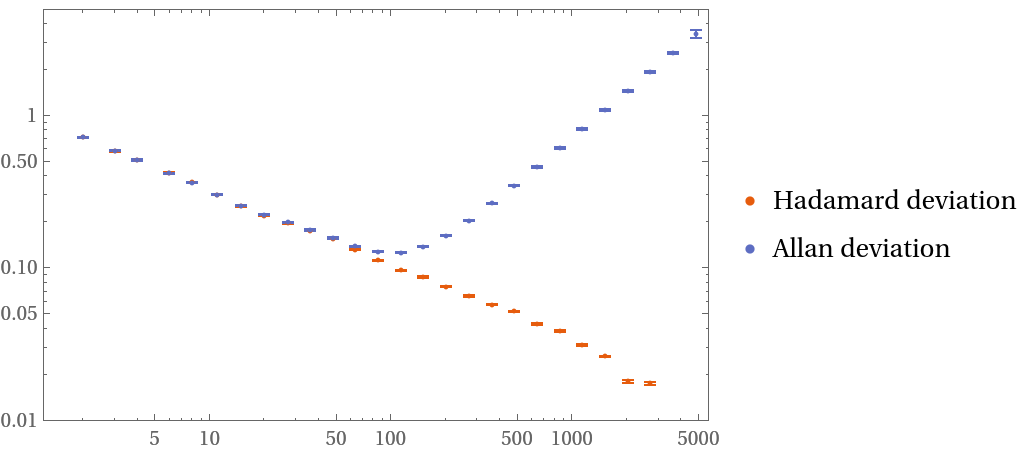Using the fast algorithm is approximately 2 times faster:

In[25]:=
data = RandomFunction[WhiteNoiseProcess[], {1000000}]["Values"]; ResourceFunction["HadamardDeviation"][data~Join~{N@Pi}, 1.0, Automatic]; // Timing
Out[26]=
In[27]:=
ResourceFunction["HadamardDeviation"][data~Join~{Pi}, 1.0, Automatic]; // Timing
Out[27]=

Possible Issues (1) 

Requesting a certain amount of samples will not necessarily result in this amount of deviations:

In[28]:=
data = RandomFunction[WhiteNoiseProcess[1], {400}]["Values"]; ResourceFunction["HadamardDeviation"][data, 1.0, {{10}}] // Length
Out[29]=

Publisher

Julien Kluge

Version History

  • 1.0.0 – 01 February 2021

Related Resources

License Information