Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Graphics3DWireFrame

Source Notebook

Get a version of 3D graphics with segments replaced by tubes

Contributed by: Enrique Zeleny

ResourceFunction["Graphics3DWireFrame"][graphics3D]

gives a version of graphics3D with segments replaced by tubes.

Details and Options

ResourceFunction["Graphics3DWireFrame"] takes the same options as Graphics3D and Tube.

Examples

Basic Examples (9) 

A surface:

In[1]:=
catalan[a_][t_][u_, v_] := {(a Cos[t]) (u - Cosh[v] Sin[u]) + (a Sin[t]) (v - Cos[u] Sinh[v]), (a Cos[t]) (1 - Cos[u] Cosh[v]) + ((a Sin[t]) Sin[u]) Sinh[ v], ((4 a) (1 - Cos[u/2] Cosh[v/2])) Sin[ t] - (((4 a) Cos[t]) Sin[u/2]) Sinh[v/2]}

Plot the surface:

In[2]:=
gr = ParametricPlot3D[ Evaluate[catalan[1][0.`][u, v]], {u, 0, 12.56`}, {v, -2, 2.`}]
Out[2]=

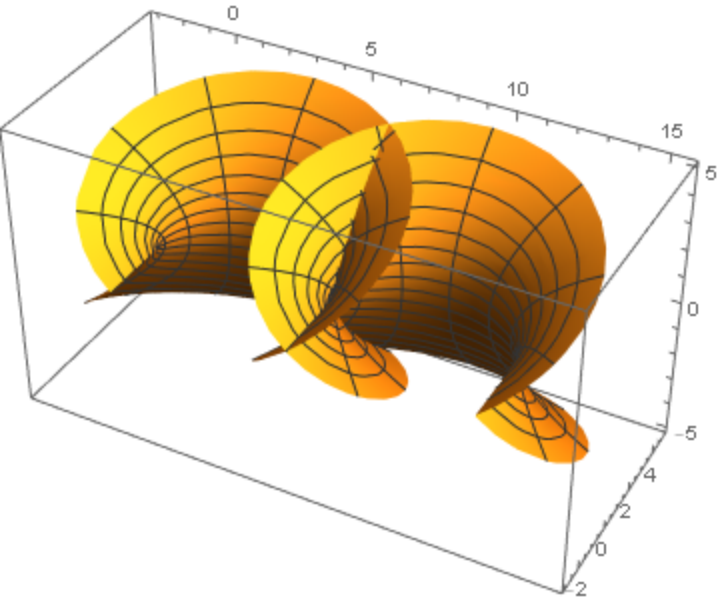
Another wire frame with a standard mesh:

In[3]:=
ResourceFunction["Graphics3DWireFrame"][ ParametricPlot3D[ Evaluate[catalan[1][0.`][u, v]], {u, 0, 12.56`}, {v, -2, 2.`}, Mesh -> Full, PlotStyle -> None], .05]
Out[3]=

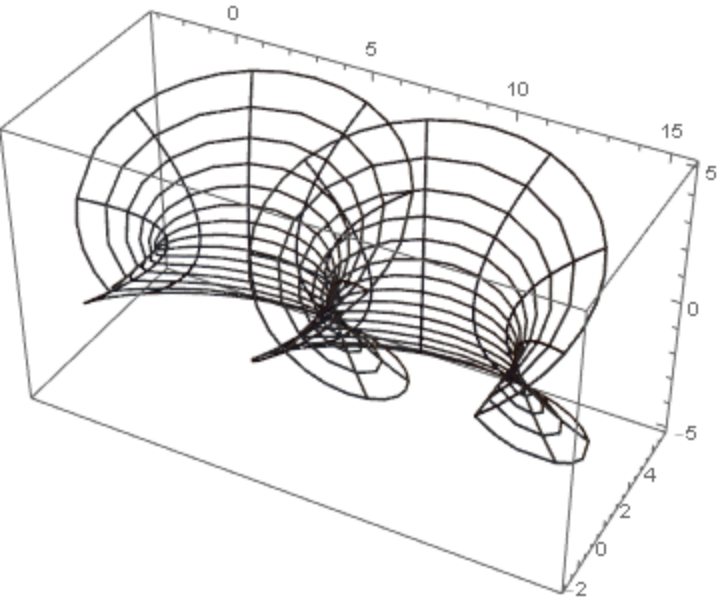
A similar appearance using PlotStyle:

In[4]:=
ParametricPlot3D[ Evaluate[catalan[1][0][u, v]], {u, 0, 12.56}, {v, -2, 2}, Boxed -> False, Axes -> False, PlotStyle -> None, MaxRecursion -> 2, Mesh -> Full]
Out[4]=

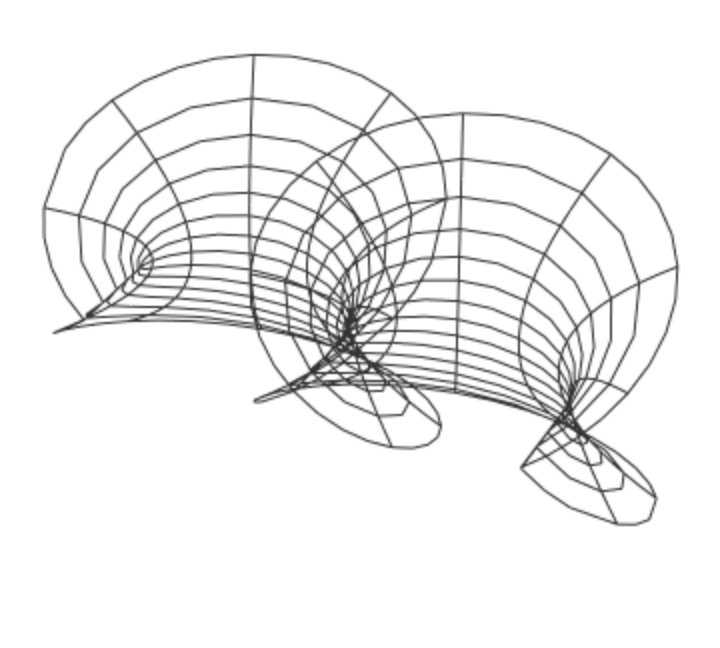
Another surface:

In[5]:=
ResourceFunction["Graphics3DWireFrame"][ ParametricPlot3D[{Cos[u], Sin[u] + Cos[v], Sin[v]}, {u, 0, 2 \[Pi]}, {v, -\[Pi], \[Pi]}, Mesh -> Full]]
Out[5]=

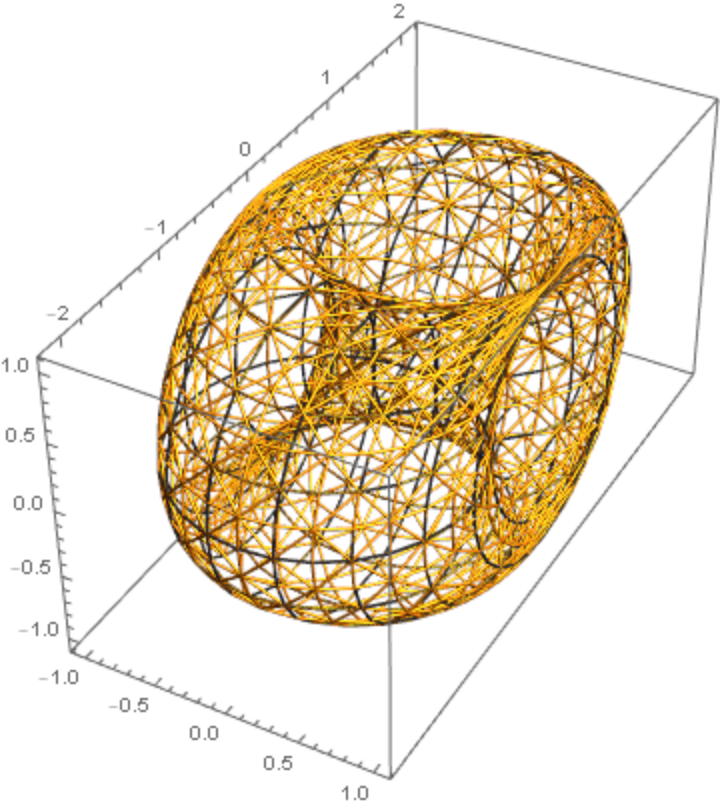
A Möbius strip made of curves:

In[6]:=
f[u_, v_] := {(1 + u Cos[v/2]) Cos[v], (1 + u Cos[v/2]) Sin[v], u Sin[v/2]}; Show[ ParametricPlot3D[ Evaluate@Table[ f[u, i], {i, -\[Pi], \[Pi], 1/6}], {u, -\[Pi], \[Pi]}, PlotRange -> All], ParametricPlot3D[ Evaluate@Table[ f[j, v], {j, -\[Pi], \[Pi], \[Pi]/3}], {v, -\[Pi], \[Pi]}]]
Out[6]=

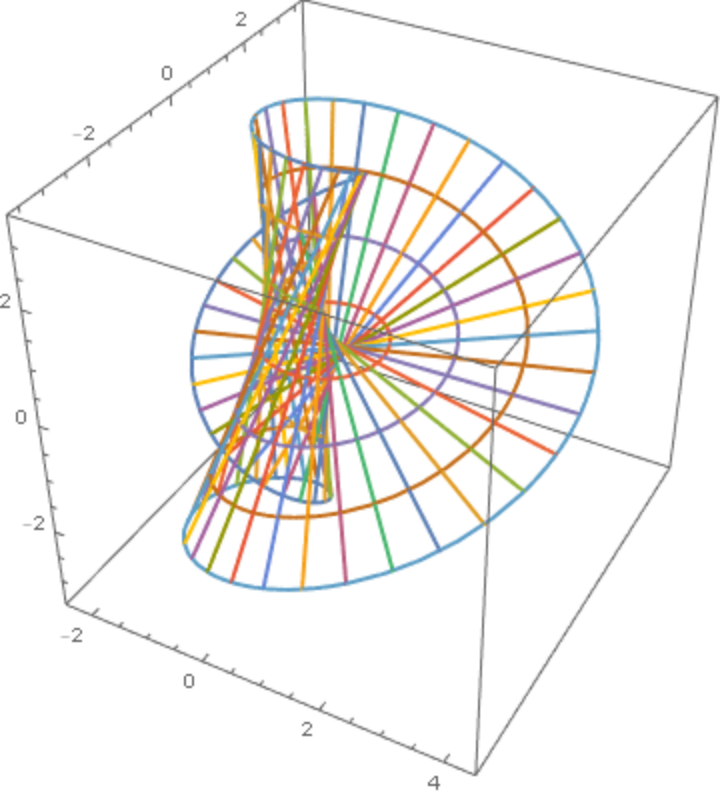
Plot the wire frame:

In[7]:=
ResourceFunction["Graphics3DWireFrame"][%, .075]
Out[7]=

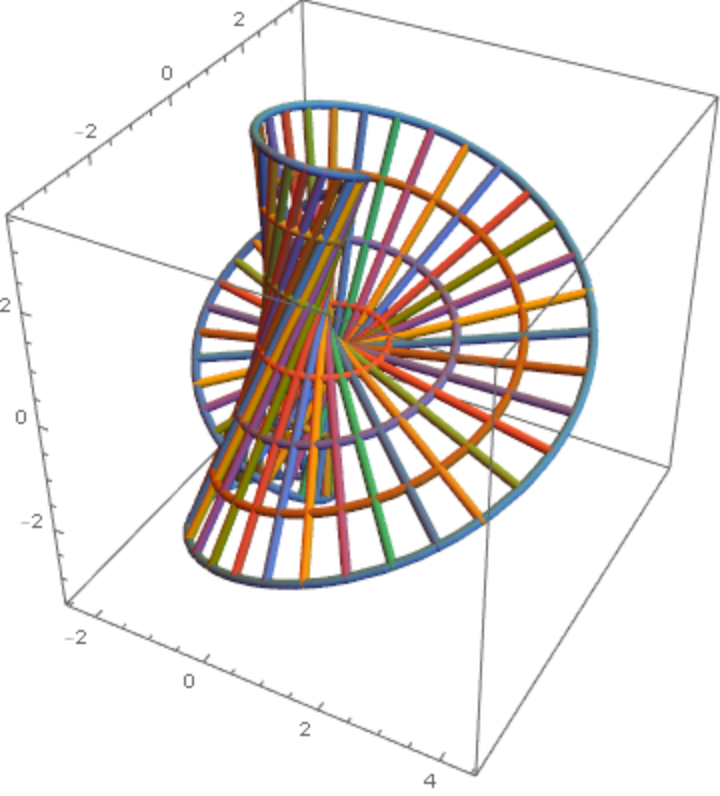
A B–spline surface:

In[8]:=
cpts = Table[{i, j, RandomReal[{-1, 1}]}, {i, 5}, {j, 5}];
In[9]:=
gr = Graphics3D[{Opacity[.75], BSplineSurface[cpts]}]
Out[9]=
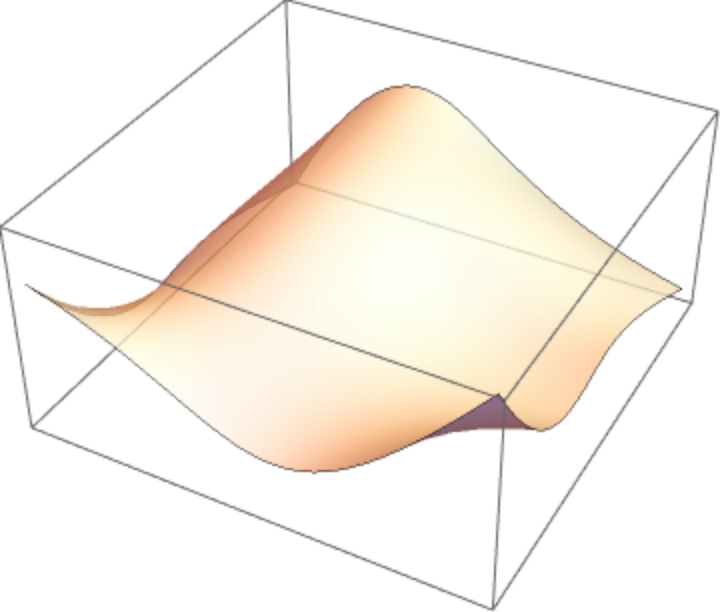
In[10]:=
Show[gr, ResourceFunction["Graphics3DWireFrame"][%, .05]]
Out[10]=

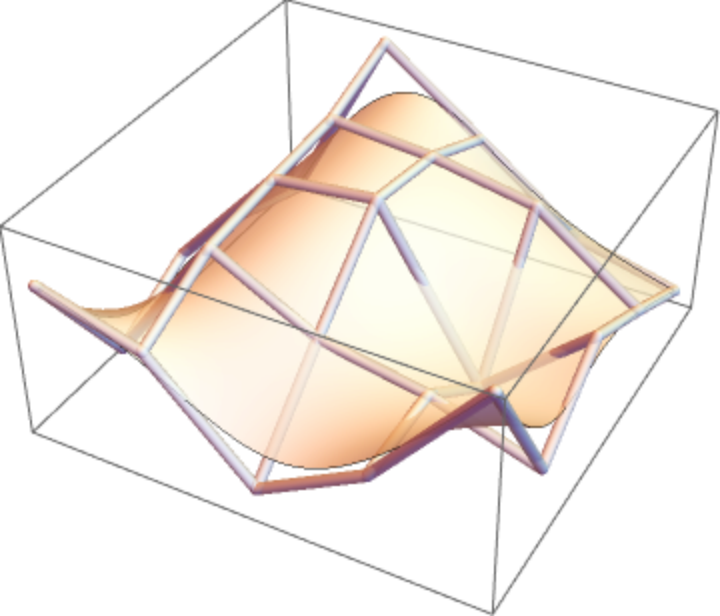
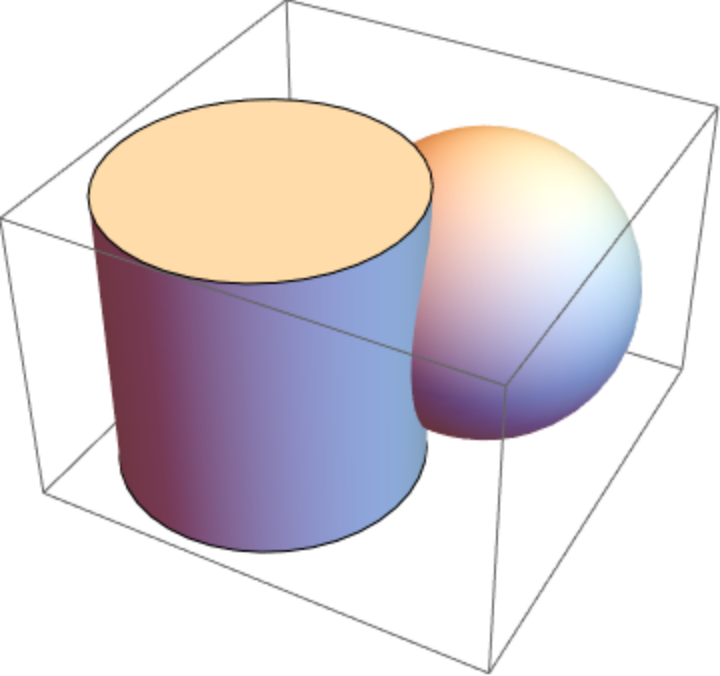
Take a region:

In[11]:=
g = Graphics3D[{Cylinder[{{2, 2, 0}, {2, 2, 2}}, 1], Sphere[{3, 3, 1}]}]
Out[11]=

Extract the primitives:

In[12]:=
DiscretizeGraphics[g, MaxCellMeasure -> {"Area" -> .1}]
Out[12]=

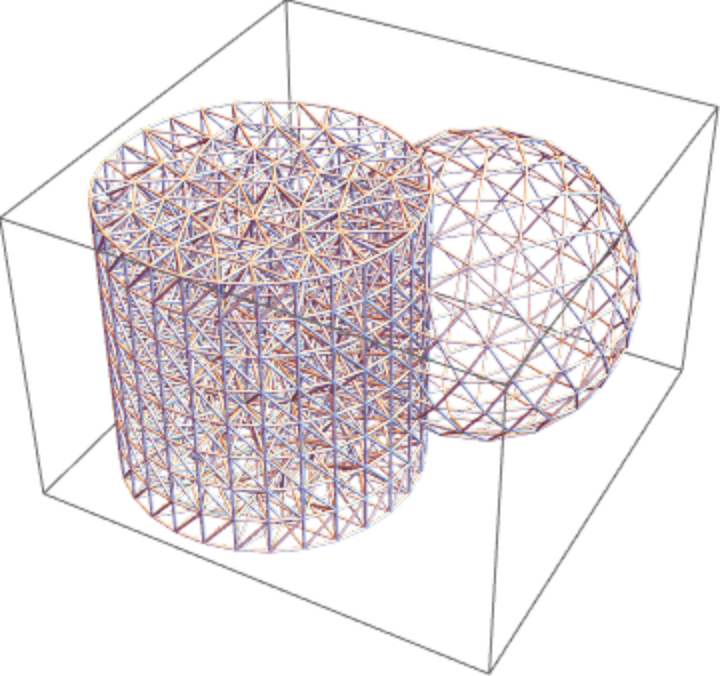
Make the wire frame:

In[13]:=
ResourceFunction["Graphics3DWireFrame"][%]
Out[13]=

A fractal region:

In[14]:=
SierpinskiMesh[4, 3]
Out[14]=
In[15]:=
ResourceFunction["Graphics3DWireFrame"][%]
Out[15]=

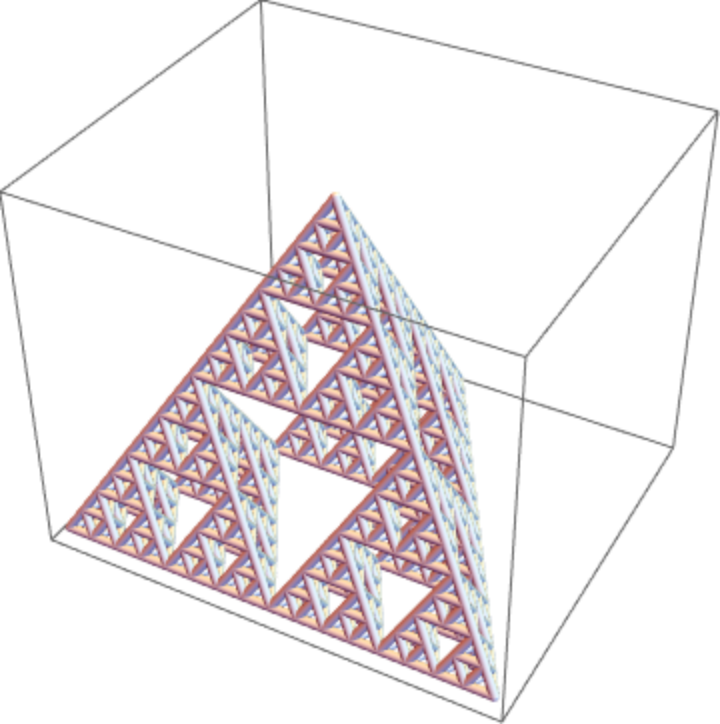
Show a dodecahedron:

In[16]:=
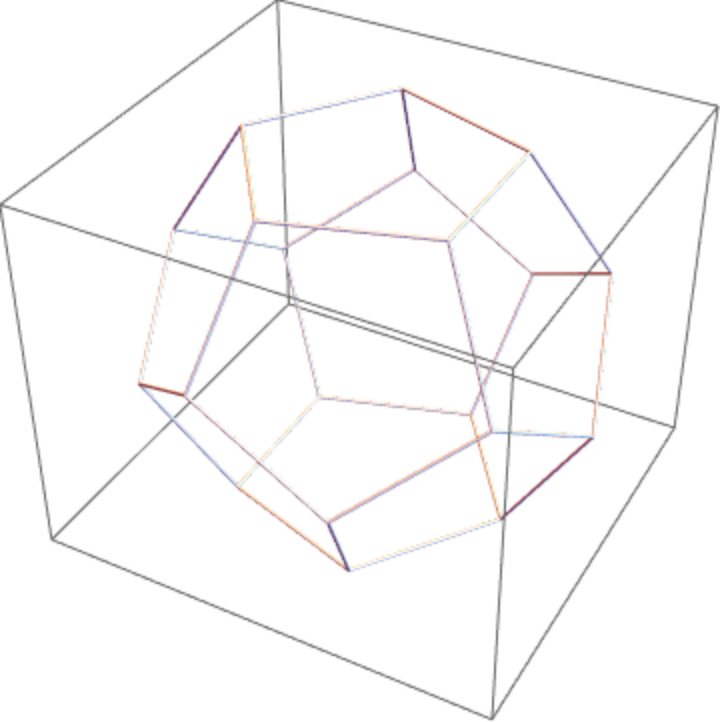
ResourceFunction["PrimitiveToPolygons"][Dodecahedron[]];

Show a dodecahedron:

In[17]:=
ResourceFunction["Graphics3DWireFrame"][Graphics3D[%]]
Out[17]=

Show a hexagonal prism:

In[18]:=
uehp = ResourceFunction["PerforatePolygons"][ Entity["Polyhedron", {"Prism", 6}]["Graphics3D"]]
Out[18]=
In[19]:=
ResourceFunction["Graphics3DWireFrame"][uehp]
Out[19]=

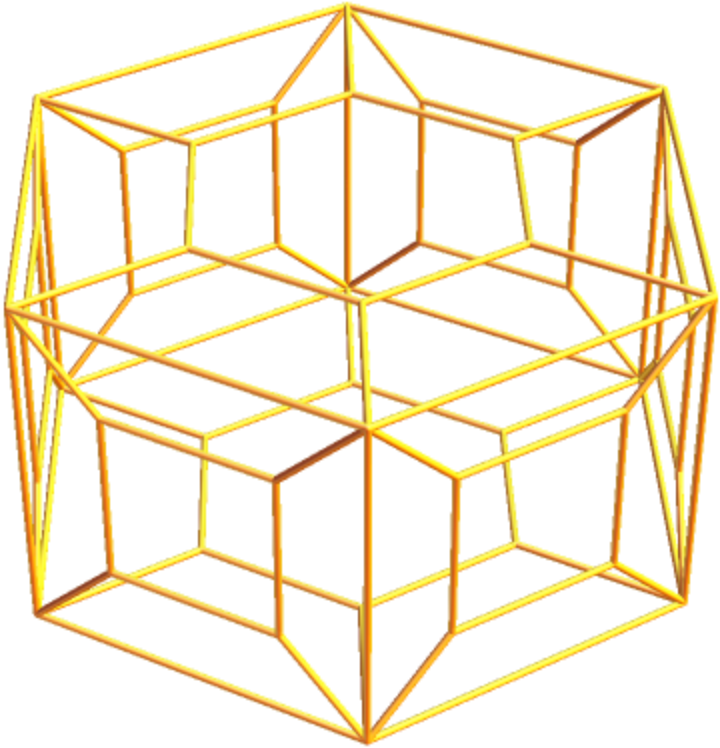
Outline the prism:

In[20]:=
uehp // ResourceFunction["OutlinePolygons"]
Out[20]=

Show a dodecahedron:

In[21]:=
ResourceFunction["Graphics3DWireFrame"][%]
Out[21]=

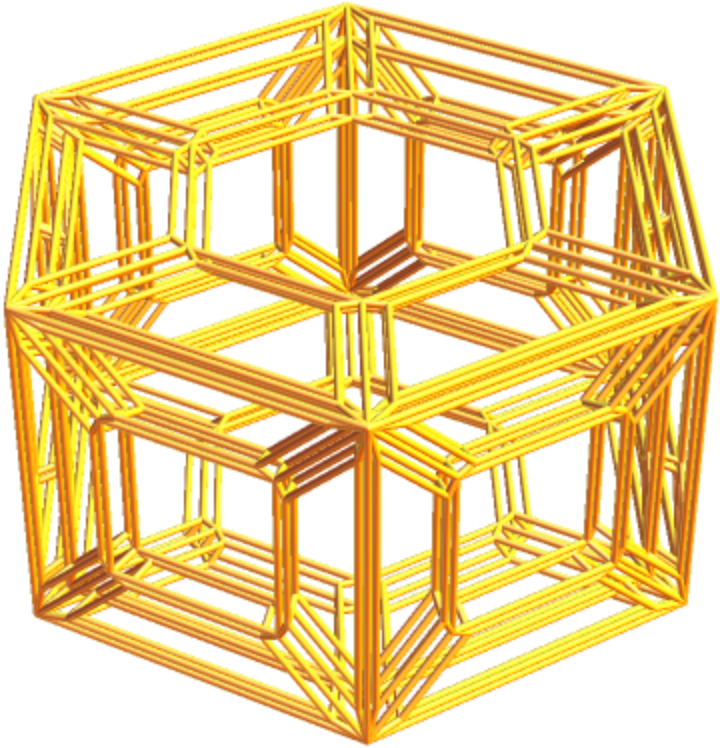
A 3D model:

In[22]:=
ResourceFunction["Graphics3DWireFrame"][ ExampleData[{"Geometry3D", "Beethoven"}], .05]
Out[22]=

Options (2) 

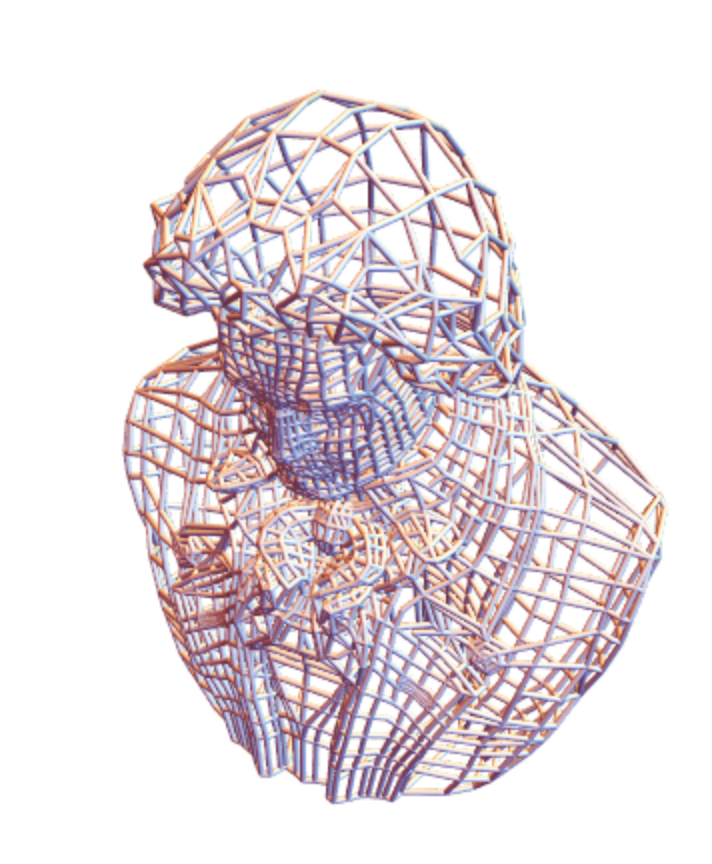
A surface:

In[23]:=
surface = ParametricPlot3D[{Cos[v] Sech[u], Sech[u] Sin[v], u - Tanh[u]}, {u, 0, 4}, {v, 0, 2 Pi}]
Out[23]=

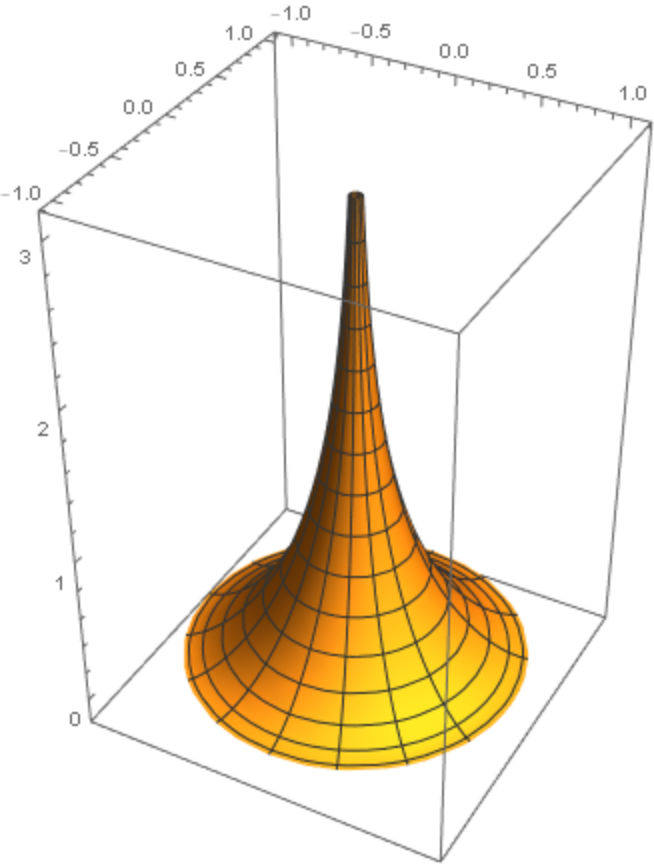
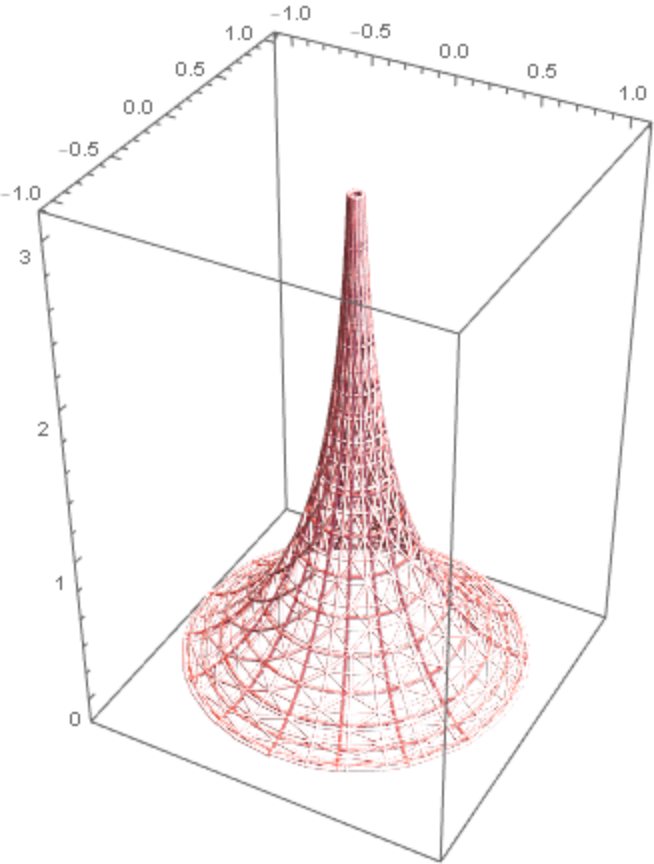
Change style of the wire frame:

In[24]:=
ResourceFunction["Graphics3DWireFrame"][surface, .01, PlotStyle -> Pink]
Out[24]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 26 April 2021

License Information