Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GraphPathMatrix

Source Notebook

Find the path matrix of a graph

Contributed by: Peter Burbery

ResourceFunction["GraphPathMatrix"][g]

gives the path matrix of the graph g.

Details

An entry pij of the path matrix is 1 if there is a path between vertex νi and vertex νj, and 0 otherwise.
The path matrix is related to the Floyd-Warshall algorithm.
ResourceFunction["GraphPathMatrix"][g,SparseArray] gives the path matrix as a SparseArray object.
An undirected connected graph will have all matrix entries equal to 1. These are not terribly interesting. The function is better suited to directed graphs where not all components are connected rather than to graphs where every vertex is reachable.

Examples

Basic Examples (2) 

Find the path matrix representation of a directed graph:

In[1]:=
ResourceFunction["GraphPathMatrix"][\!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{$CellContext`\[ScriptCapitalA], $CellContext`\[ScriptCapitalB], $CellContext`\[ScriptCapitalC], $CellContext`\[ScriptCapitalE], $CellContext`\[ScriptCapitalD], $CellContext`\[ScriptCapitalG], $CellContext`\[ScriptCapitalH]}, {{{1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 6}, {6, 2}, {3, 7}, {1, 7}}, Null}, {VertexShapeFunction -> {"Name"}}]]}, TagBox[GraphicsGroupBox[ GraphicsComplexBox[{{2.733309926992625, 1.139507749446123}, { 1.7120684494104554`, 1.196328991389978}, { 1.7120466999747426`, 0.22094561816968322`}, { 0.6414468573710435, 0.}, {0., 0.7087881142831897}, { 0.6411100015694988, 1.4170433452358484`}, { 2.731194525723913, 0.2772567560767854}}, { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{1, 2}, {1, 7}, {2, 3}, {3, 4}, {3, 7}, {4, 5}, {5, 6}, {6, 2}}, 0.05659194539806142]}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], InsetBox[ PaneBox["\[ScriptCapitalA]", Alignment->Center, ImageMargins->2], 1, BaseStyle->"Graphics"], InsetBox[ PaneBox["\[ScriptCapitalB]", Alignment->Center, ImageMargins->2], 2, BaseStyle->"Graphics"], InsetBox[ PaneBox["\[ScriptCapitalC]", Alignment->Center, ImageMargins->2], 3, BaseStyle->"Graphics"], InsetBox[ PaneBox["\[ScriptCapitalE]", Alignment->Center, ImageMargins->2], 4, BaseStyle->"Graphics"], InsetBox[ PaneBox["\[ScriptCapitalD]", Alignment->Center, ImageMargins->2], 5, BaseStyle->"Graphics"], InsetBox[ PaneBox["\[ScriptCapitalG]", Alignment->Center, ImageMargins->2], 6, BaseStyle->"Graphics"], InsetBox[ PaneBox["\[ScriptCapitalH]", Alignment->Center, ImageMargins->2], 7, BaseStyle->"Graphics"]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FormatType->TraditionalForm, FrameTicks->None]\)] // MatrixForm
Out[1]=

A random graph:

In[2]:=
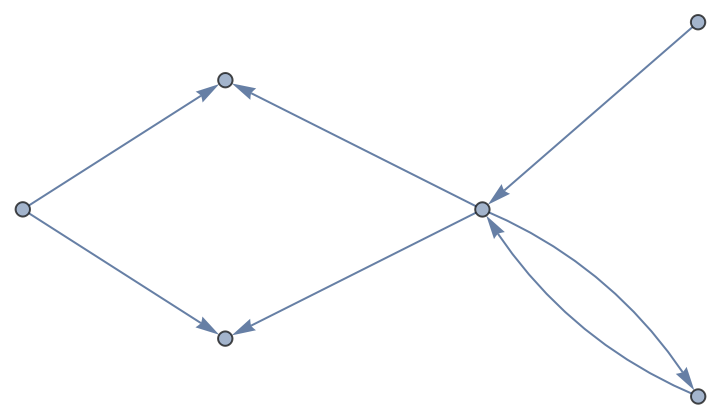
ResourceFunction["GraphPathMatrix"][ Echo[RandomGraph[{6, 7}, DirectedEdges -> True]]] // MatrixForm
Out[2]=

Scope (13) 

A directed graph generated from the Price graph distribution:

In[3]:=
ResourceFunction["GraphPathMatrix"][ Echo[DirectedGraph[RandomGraph[PriceGraphDistribution[7, 2, 1]], "Random"]]] // MatrixForm
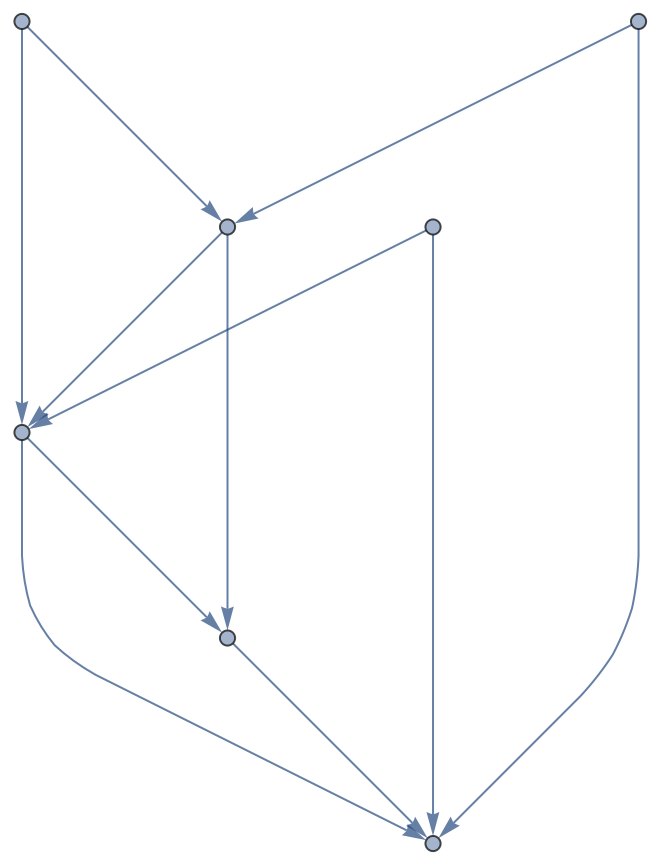
Out[3]=

Random cycle graph:

In[4]:=
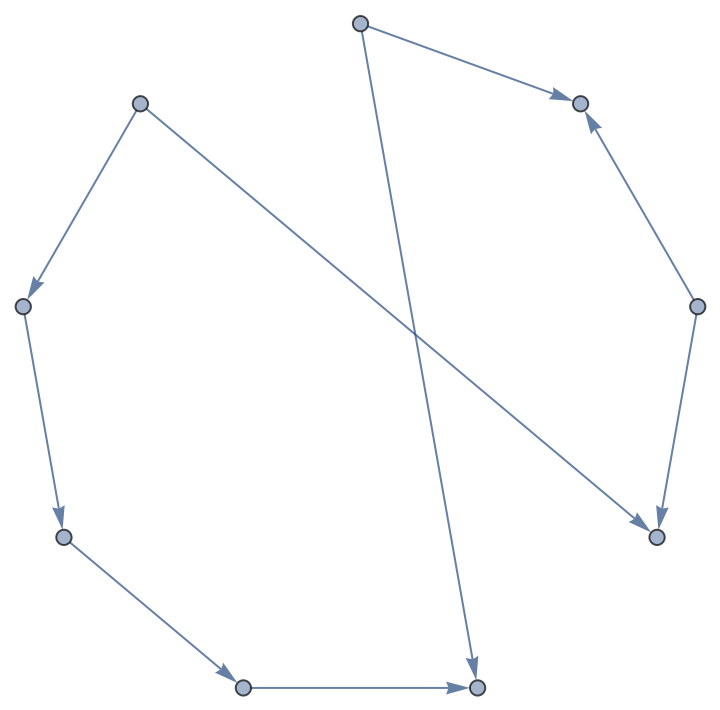
ResourceFunction["GraphPathMatrix"][ Echo[DirectedGraph[CycleGraph[9], "Random"]]] // MatrixForm
Out[4]=

Directed graph from graph product:

In[5]:=
ResourceFunction["GraphPathMatrix"][ Echo[DirectedGraph[GraphProduct[\!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2, 3, 4}, {Null, {{1, 2}, {2, 3}, {3, 4}, {4, 1}}}, {FrameTicks -> None, VertexCoordinates -> {{1., 6.123233995736766*^-17}, { 1.2246467991473532`*^-16, -1.}, {-1., -1.8369701987210297`*^-16}, {-2.4492935982947064`*^-16, 1.}}}]], Typeset`boxes = GraphicsGroupBox[{{ Directive[ Hue[0.6, 0.2, 0.8], EdgeForm[ Directive[ GrayLevel[0], Opacity[0.7]]]], TagBox[ DiskBox[{1., 6.123233995736766*^-17}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$1"], TagBox[ DiskBox[{1.2246467991473532`*^-16, -1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$2"], TagBox[ DiskBox[{-1., -1.8369701987210297`*^-16}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$3"], TagBox[ DiskBox[{-2.4492935982947064`*^-16, 1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$4"]}, { Directive[ Opacity[0.7], Hue[0.6, 0.7, 0.5]], LineBox[{{ DynamicLocation["VertexID$1", Automatic, Center], DynamicLocation["VertexID$2", Automatic, Center]}, { DynamicLocation["VertexID$1", Automatic, Center], DynamicLocation["VertexID$4", Automatic, Center]}, { DynamicLocation["VertexID$2", Automatic, Center], DynamicLocation["VertexID$3", Automatic, Center]}, { DynamicLocation["VertexID$3", Automatic, Center], DynamicLocation["VertexID$4", Automatic, Center]}}]}}]}, DynamicBox[GraphComputation`NetworkGraphicsBox[ 1, Typeset`graph, Typeset`boxes], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {}}, ImageSizeCache->{{0.13407836914062776`, 56.56984008789062}, {-30.524476953124996`, 25.911284765625}}]]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FrameTicks->None, ImageSize->{56.70391845703125, Automatic}]\), \!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2}, {Null, {{1, 2}}}]], Typeset`deleteGraphTag}, TagBox[GraphicsComplexBox[{{1., 0.}, {-1., 0.}}, { {Hue[0.6, 0.7, 0.5], Opacity[0.7], {Arrowheads[0.], ArrowBox[{1, 2}, 0.02261146496815286]}}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.02261146496815286], DiskBox[2, 0.02261146496815286]}}], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FormatType->TraditionalForm, FrameTicks->None]\)], "Random"]]] // MatrixForm
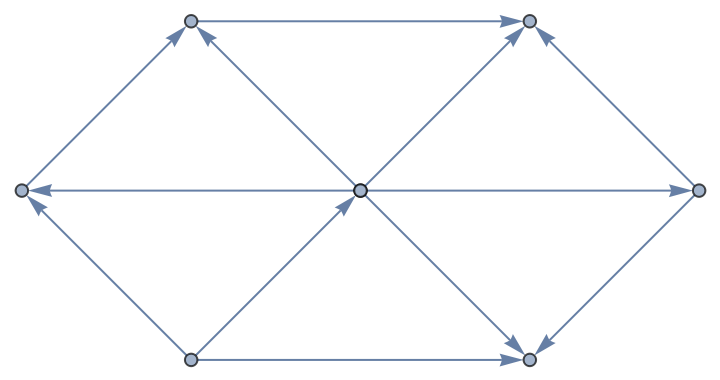
Out[5]=

Directed graph from graph product of multigraphs:

In[6]:=
ResourceFunction["GraphPathMatrix"][ Echo[DirectedGraph[GraphProduct[\!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2, 3, 4}, {{{1, 2}, {1, 2}, {2, 3}, {1, 4}, {3, 4}}, Null}, {EdgeStyle -> { Arrowheads[0.1]}}]], Typeset`deleteGraphTag}, TagBox[GraphicsComplexBox[CompressedData[" 1:eJxdk38s1GEcx7/nOMrEFJKl5bYUwvIrm+7zbHZ+LPOrTmhr2KEZo7WpxYZC GaHOVlL+iHH9wmUZRz3D/Fq5rBolSc6M7txxorkd5ew85nnv+92z1/N8nuf7 ee2752hSZnSyEcMwoZuvftwdM0RNULwIu0d6frt+p85qMN7ZeuEpDBWO9LQ6 myJ0TTowltgII/yszPJFDkKvuIrHri9AuephUdvOQQk3B5K4IU1wdnZGys7n oEHv4qGh+BYoiDLSTQVxUGylsI/nL4HJZ931Fyw4qCW+QqV8J4F7Jg79JZ9N 0GJUu2ORQgLVW9nh1BR9jEh9pnbGP9vNiJzHjeFdFGtY5Ht5TevsIx0sFGno p83ega/LYyFPQ782e0Y0icGbbPDxlFZUXrFkIcbg65fjcSbsK4MM/pjyx5Q/ pvwx5Y8pf0z5Y8ofU/6Y8seUP6b8MeWPKX9M+WPKH2/7V1v4+dT1iGGI63p1 5bEpcmx+eW68Vwp3HiWd/HXCFN3oqrYZFvWBv7DBvbeBg45rHlSG9MtgMn81 u2Y/B4XlXh5uzv0C2YvRnLQsEzST6nSoxHYcjFs7J9zfGiP1jwC72INTUDjo qZ1fY6PDAX5F95PlsOb5+lLNMTbKCWfGljWzkKiEvYGBm74igQ18m4NTfGtn EWYhWaEg7Hzxb1AHldSu+rDQtBOT66VVwMOl+qyMBgZVZAjqJ7wXwIWf/OSv FYNGhYK+CF8VRN6qCnVRbECHGfOzbEMFTrJGizLxOvjGCZZEd9UwmGZ8+0C8 DsJjBDqhXA3Bcc/f9P7Tknux9TtSVgnXRWjrI7R/CMtPl28+y8AyMNdJHw1Z TzRvSzBv27lnMC/izYtUhLs69VEQ9tcfJ58jrN+dYD5L2GsrcsK1ktIxyJwi LLMsrSpo/E76sUvvtk3vHiXr9telPuD2ibA4VTm98vE94SqevsFewlPzo7qW kA7CGy4fSvaZiOE/rUjWKw== "], { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.1], ArrowBox[ BezierCurveBox[{1, {0.16444074718311652`, 2.4999999999999996`}, 2}], 0.030239520958083826`], ArrowBox[ BezierCurveBox[{1, {-0.16444074718311652`, 2.4999999999999996`}, 2}], 0.030239520958083826`], ArrowBox[ BezierCurveBox[{1, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 4}], 0.030239520958083826`], ArrowBox[{2, 3}, 0.030239520958083826`], ArrowBox[{3, 4}, 0.030239520958083826`]}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.030239520958083826], DiskBox[2, 0.030239520958083826], DiskBox[3, 0.030239520958083826], DiskBox[4, 0.030239520958083826]}}], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FormatType->TraditionalForm, FrameTicks->None]\), \!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2}, {{{1, 2}, {1, 2}}, Null}, {EdgeStyle -> { Arrowheads[0.08]}}]], Typeset`deleteGraphTag}, TagBox[GraphicsComplexBox[CompressedData[" 1:eJxTTMoPSmViYGBQAmIQDQEf7BnQAHuMiLHasoU2ysJO3OfnvbEXOBGlLvR2 0X578YN7LQ+9tnco33X8euLy/Wtv7zepePTK3mGt8us52qv3a82c/JqP4ZV9 QtPxJGWPdftZ3Dg/NEu/tD9h0nbyZNSG/WXL2SbHmb6wj5iQctTOcuN+F7Ec CXW/5/Ybovrfvdm3cX9KGgg8s/8QuEOu9fXG/cZgcNn+BZRffFn9/Mbki/Yr oOoVkp5ubtU6bx8ANe/581v2Hyaetj8Atc9/9sbAI/+P2ztA3eM8kUFXvuyI vQLUvf8W/eaQ/H7AXgHqn6tp75e2c+62/3Ac4l80/9uj+d8ezf/2aP63R/O/ PZr/7dH8b4/mf3uY/39A+TD/74CqV4L6PwFq3kuo/y9A7QuE+h/mHleo/2Hu hfkf5p/rUP/D/AsAKn8GqA== "], { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.08], ArrowBox[ BezierCurveBox[{1, { 0.5000000000000006, -0.16444074718311627`}, 2}], 0.01273], ArrowBox[ BezierCurveBox[{1, {0.5000000000000001, 0.16444074718311646`}, 2}], 0.01273]}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.01273], DiskBox[2, 0.01273]}}], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FormatType->TraditionalForm, FrameTicks->None, ImageSize->{89.27401733398438, Automatic}]\)], "Random"]]] // MatrixForm
Out[6]=

A parametric k-ary tree graph:

In[7]:=
ResourceFunction["GraphPathMatrix"][ Echo[DirectedGraph[KaryTree[10], "Random"]]] // MatrixForm
Out[7]=

A parametric complete k-ary tree graph:

In[8]:=
ResourceFunction["GraphPathMatrix"][ Echo[DirectedGraph[CompleteKaryTree[3, 3], "Random"]]] // MatrixForm
Out[8]=

A random directed graph:

In[9]:=
ResourceFunction["GraphPathMatrix"][Echo[DirectedGraph[\!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2, 3, 4}, {Null, {{1, 2}, {2, 3}, {3, 1}, {3, 4}}}, {EdgeStyle -> { Arrowheads[0.06]}}]]}, TagBox[GraphicsGroupBox[ GraphicsComplexBox[{{0.0001964751172666146, 0.}, {0., 0.8475386976306538}, {0.9164048379140673, 0.42386488156829044`}, {2.031430211699506, 0.42382043094346533`}}, { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.06], {Arrowheads[0.], ArrowBox[{1, 2}, 0.022865977658369868`]}, {Arrowheads[0.], ArrowBox[{1, 3}, 0.022865977658369868`]}, {Arrowheads[0.], ArrowBox[{2, 3}, 0.022865977658369868`]}, {Arrowheads[0.], ArrowBox[{3, 4}, 0.022865977658369868`]}}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.022865977658369868], DiskBox[2, 0.022865977658369868], DiskBox[3, 0.022865977658369868], DiskBox[4, 0.022865977658369868]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FrameTicks->None, GridLinesStyle->Directive[ GrayLevel[0.5, 0.4]]]\), "Random"]]] // MatrixForm
Out[9]=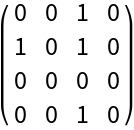

An acyclic directed graph:

In[10]:=
ResourceFunction["GraphPathMatrix"][Echo[DirectedGraph[\!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2, 3, 4}, {Null, {{1, 2}, {2, 3}, {3, 1}, {3, 4}}}, {EdgeStyle -> { Arrowheads[0.06]}}]]}, TagBox[GraphicsGroupBox[ GraphicsComplexBox[{{0.0001964751172666146, 0.}, {0., 0.8475386976306538}, {0.9164048379140673, 0.42386488156829044`}, {2.031430211699506, 0.42382043094346533`}}, { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.06], {Arrowheads[0.], ArrowBox[{1, 2}, 0.022865977658369868`]}, {Arrowheads[0.], ArrowBox[{1, 3}, 0.022865977658369868`]}, {Arrowheads[0.], ArrowBox[{2, 3}, 0.022865977658369868`]}, {Arrowheads[0.], ArrowBox[{3, 4}, 0.022865977658369868`]}}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.022865977658369868], DiskBox[2, 0.022865977658369868], DiskBox[3, 0.022865977658369868], DiskBox[4, 0.022865977658369868]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FrameTicks->None, GridLinesStyle->Directive[ GrayLevel[0.5, 0.4]]]\), "Acyclic"]]] // MatrixForm
Out[10]=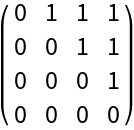

Another acyclic directed graph:

In[11]:=
ResourceFunction["GraphPathMatrix"][Echo[DirectedGraph[\!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{2, 1, 3, 4}, {{{1, 2}, {3, 2}, {4, 2}}, {{1, 3}, {3, 4}}}, {EdgeStyle -> { Arrowheads[0.08]}}]]}, TagBox[GraphicsGroupBox[ GraphicsComplexBox[{{0., 0.43424724174389495`}, { 0.9342311127898241, 0.8686478533594477}, { 0.9340813306102785, 0.}, {1.868395490083372, 0.43417761049629644`}}, { {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.08], StyleBox[{LineBox[{1, 3}], ArrowBox[{1, 2}, 0.02153460989130551], LineBox[{3, 4}], ArrowBox[{3, 2}, 0.02153460989130551], ArrowBox[{4, 2}, 0.02153460989130551]}, FontFamily->"Arial"]}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], StyleBox[{DiskBox[1, 0.02153460989130551], DiskBox[2, 0.02153460989130551], DiskBox[3, 0.02153460989130551], DiskBox[4, 0.02153460989130551]}, FontFamily->"Arial"]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], BaseStyle->(FontFamily -> "Arial"), DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FrameTicks->None, GridLinesStyle->Directive[ GrayLevel[0.5, 0.4]], ImageSize->{102.7890625, Automatic}, LabelStyle->{FontFamily -> "Arial"}]\), "Acyclic"]]] // MatrixForm
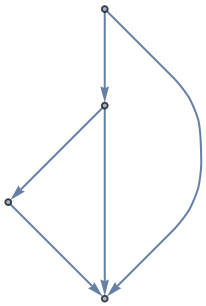
Out[11]=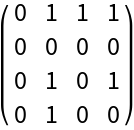

A random Bernoulli graph:

In[12]:=
ResourceFunction["GraphPathMatrix"][ Echo[DirectedGraph[RandomGraph[BernoulliGraphDistribution[10, 0.3]], "Random"]]] // MatrixForm
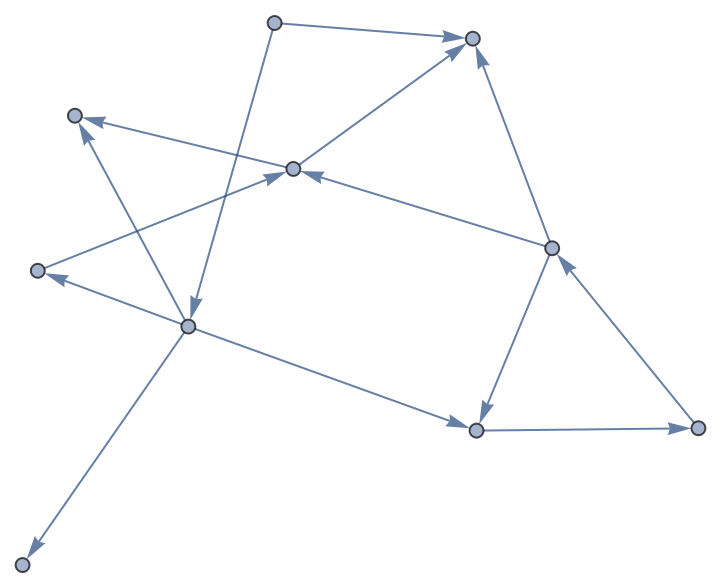
Out[12]=

A random disconnected spatial directed graph with random orientations for the directed edges:

In[13]:=
ResourceFunction["GraphPathMatrix"][ Echo[DirectedGraph[RandomGraph[SpatialGraphDistribution[15, 0.3]], "Random"]]] // MatrixForm
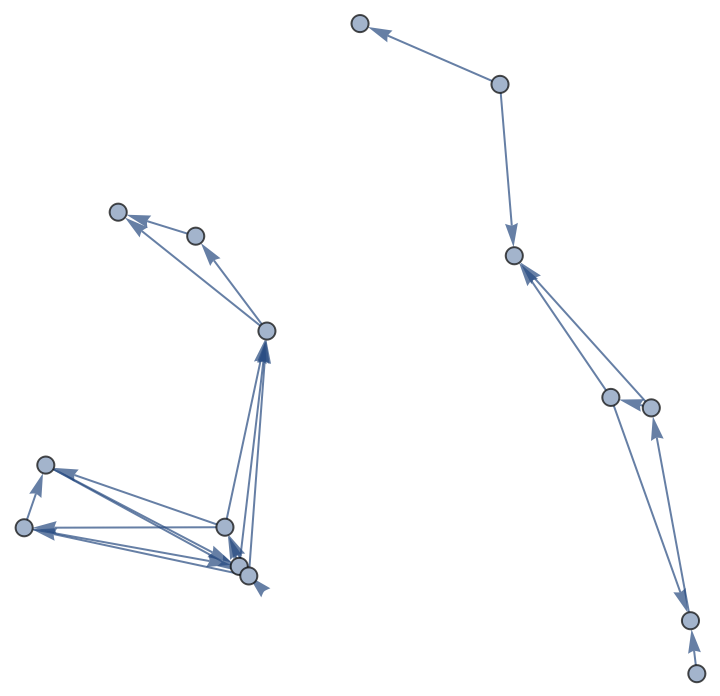
Out[13]=

Find the path matrix representation of the Petersen graph with script capital letters for the vertex names:

In[14]:=
petersenGraph = PetersenGraph[ VertexLabels -> Thread[Range[ 10] -> {\[ScriptCapitalA], \[ScriptCapitalB], \[ScriptCapitalC], \[ScriptCapitalD], \[ScriptCapitalE], \[ScriptCapitalF], \[ScriptCapitalG], \[ScriptCapitalH], \[ScriptCapitalI], \[ScriptCapitalJ]}]]
Out[14]=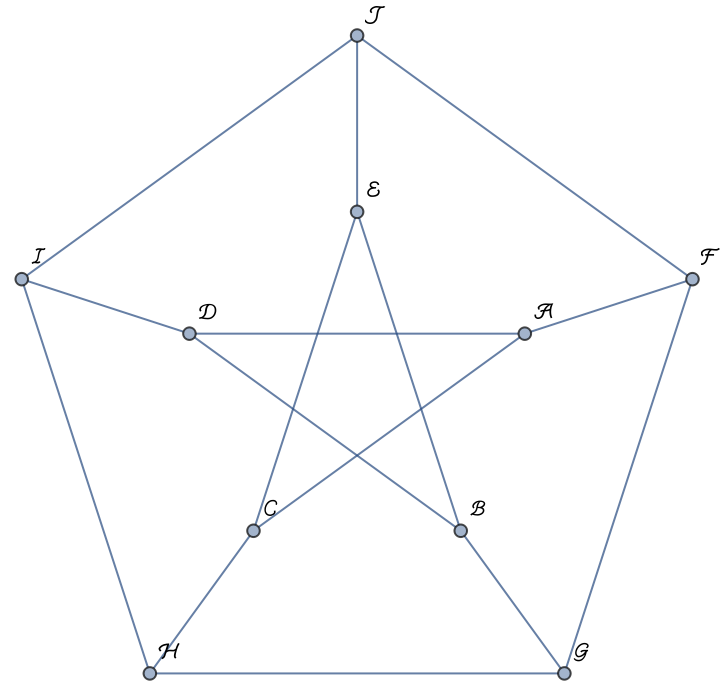

Find the path matrix representation of the undirected graph:

In[15]:=
ResourceFunction["GraphPathMatrix"][petersenGraph] // MatrixForm
Out[15]=

Output the matrix as a sparse array for efficiency:

In[16]:=
g = DirectedGraph[GridGraph[{5, 10}], "Random"]; ResourceFunction["GraphPathMatrix"][g, "SparseArray"]
Out[17]=

Publisher

Peter Burbery

Requirements

Wolfram Language 13.2 (December 2022) or above

Version History

  • 1.0.0 – 02 June 2023

Author Notes

The function often generates a matrix with all 1s.

License Information