Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Graph
Find the volumes of successively larger neighborhoods around nodes in a graph
Contributed by:
Max Piskunov, Stephen Wolfram and Jan Mangaldan
ResourceFunction["GraphNeighborhoodVolumes"][graph] gives the numbers of neighbors within successive distances for each vertex in graph. | |
ResourceFunction["GraphNeighborhoodVolumes"][graph,{v1,v2,…}] finds the numbers for the vertices vi. | |
ResourceFunction["GraphNeighborhoodVolumes"][graph,All,r] finds the numbers of neighbors for all vertices out to maximum radius r. | |
ResourceFunction["GraphNeighborhoodVolumes"][graph,vi,Automatic] finds the numbers of neighbors only out to the minimum radius for any of the vertices vi. | |
ResourceFunction["GraphNeighborhoodVolumes"][graph,"Random"→n,…] finds the numbers of neighbors for n randomly chosen vertices. |
Details and Options
ResourceFunction["GraphNeighborhoodVolumes"] works with both directed and undirected graphs. For directed graphs, it takes the volume around a given vertex to be the number of vertices reachable by following directed edges.
ResourceFunction["GraphNeighborhoodVolumes"] accepts the option "Padded", which is False by default. When set to True, ResourceFunction["GraphNeighborhoodVolumes"] finds the numbers of neighbors out to the maximum radius of the graph (or an integer less than the maximum radius) for the specified vertices, padding any vertex of submaximal radius with its final volume value.
ResourceFunction["GraphNeighborhoodVolumes"] uses ParallelMap.
Examples
Basic Examples (4)
In a complete graph, the volume around each node includes every node after one step:
| In[1]:= |
![ResourceFunction["GraphNeighborhoodVolumes"][CompleteGraph[5]]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/1233c81c1c13eac0.png){kind=small}
|
| Out[1]= |
|
In this graph, the volume grows linearly with the radius:
| In[2]:= |
![ResourceFunction["GraphNeighborhoodVolumes"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6}, {Null,
SparseArray[
Automatic, {6, 6}, 0, {
1, {{0, 2, 4, 6, 8, 10, 12}, {{6}, {2}, {1}, {3}, {2}, {
4}, {3}, {5}, {4}, {6}, {5}, {1}}}, Pattern}]}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{-0.8660254037844389, 0.5000000000000007}, {-0.8660254037844384, \
-0.4999999999999994}, {3.8285686989269494`*^-16, -1.}, {
0.8660254037844389, -0.5000000000000012}, {
0.8660254037844386, 0.4999999999999993}, {
1.8369701987210297`*^-16, 1.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 6}, {1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 6}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.02261146496815286], DiskBox[2, 0.02261146496815286], DiskBox[3, 0.02261146496815286], DiskBox[4, 0.02261146496815286], DiskBox[5, 0.02261146496815286], DiskBox[6, 0.02261146496815286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "f4e18a29-f070-4269-a1f9-fbcb8a3d61fb",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{85.859375, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/282f2b0d459eddb4.png)
|
| Out[2]= |
|
Limit to distance 2:
| In[3]:= |
![ResourceFunction["GraphNeighborhoodVolumes"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6}, {Null,
SparseArray[
Automatic, {6, 6}, 0, {
1, {{0, 2, 4, 6, 8, 10, 12}, {{6}, {2}, {1}, {3}, {2}, {
4}, {3}, {5}, {4}, {6}, {5}, {1}}}, Pattern}]}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{-0.8660254037844389, 0.5000000000000007}, {-0.8660254037844384, \
-0.4999999999999994}, {3.8285686989269494`*^-16, -1.}, {
0.8660254037844389, -0.5000000000000012}, {
0.8660254037844386, 0.4999999999999993}, {
1.8369701987210297`*^-16, 1.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 6}, {1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 6}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.02261146496815286], DiskBox[2, 0.02261146496815286], DiskBox[3, 0.02261146496815286], DiskBox[4, 0.02261146496815286], DiskBox[5, 0.02261146496815286], DiskBox[6, 0.02261146496815286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "cd2928c0-b6f5-4b9c-8b60-c82fd6a3a472",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{85.859375, Automatic}]\), All, 2]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/63c21cf1cd59fffc.png)
|
| Out[3]= |
|
In this graph, the volume basically grows exponentially with the radius:
| In[4]:= |
![ResourceFunction["GraphNeighborhoodVolumes"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {Null,
SparseArray[
Automatic, {10, 10}, 0, {
1, {{0, 2, 5, 8, 11, 13, 14, 15, 16, 17, 18}, {{2}, {3}, {
1}, {4}, {5}, {1}, {6}, {7}, {2}, {8}, {9}, {2}, {10}, {
3}, {3}, {4}, {4}, {5}}}, Pattern}]}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{1.9280537607514543`, 2.4354363293702583`}, {1.0147651372376076`, 1.6236242195801722`}, {2.8413423842653014`, 1.6236242195801722`}, {0.405906054895043, 0.8118121097900863}, {1.623624219580172, 0.8118121097900863}, {2.4354363293702583`, 0.8118121097900863}, {3.247248439160344, 0.8118121097900863}, {0., 0.}, {0.811812109790086, 0.}, {
1.623624219580172, 0.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {1, 3}, {2, 4}, {2, 5}, {3, 6}, {3, 7}, {
4, 8}, {4, 9}, {5, 10}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.03198674214401906], DiskBox[2, 0.03198674214401906], DiskBox[3, 0.03198674214401906], DiskBox[4, 0.03198674214401906], DiskBox[5, 0.03198674214401906], DiskBox[6, 0.03198674214401906], DiskBox[7, 0.03198674214401906], DiskBox[8, 0.03198674214401906], DiskBox[9, 0.03198674214401906], DiskBox[10, 0.03198674214401906]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "c6e9b35f-c856-4808-a0cf-2f210ee3d879",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/17682b2138bac363.png)
|
| Out[4]= |
|
Demonstrating the padded volume of the same graph:
| In[5]:= |
![ResourceFunction["GraphNeighborhoodVolumes"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {Null,
SparseArray[
Automatic, {10, 10}, 0, {
1, {{0, 2, 5, 8, 11, 13, 14, 15, 16, 17, 18}, {{2}, {3}, {
1}, {4}, {5}, {1}, {6}, {7}, {2}, {8}, {9}, {2}, {10}, {
3}, {3}, {4}, {4}, {5}}}, Pattern}]}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{1.9280537607514543`, 2.4354363293702583`}, {1.0147651372376076`, 1.6236242195801722`}, {2.8413423842653014`, 1.6236242195801722`}, {0.405906054895043, 0.8118121097900863}, {1.623624219580172, 0.8118121097900863}, {2.4354363293702583`, 0.8118121097900863}, {3.247248439160344, 0.8118121097900863}, {0., 0.}, {0.811812109790086, 0.}, {
1.623624219580172, 0.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {1, 3}, {2, 4}, {2, 5}, {3, 6}, {3, 7}, {
4, 8}, {4, 9}, {5, 10}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.03198674214401906], DiskBox[2, 0.03198674214401906], DiskBox[3, 0.03198674214401906], DiskBox[4, 0.03198674214401906], DiskBox[5, 0.03198674214401906], DiskBox[6, 0.03198674214401906], DiskBox[7, 0.03198674214401906], DiskBox[8, 0.03198674214401906], DiskBox[9, 0.03198674214401906], DiskBox[10, 0.03198674214401906]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "c6e9b35f-c856-4808-a0cf-2f210ee3d879",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), All, "Padded" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/133e27fbd1a8c003.png)
|
| Out[5]= |
|
The padded volume can also be taken for an integer less than the maximum graph radius:
| In[6]:= |
![ResourceFunction["GraphNeighborhoodVolumes"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {Null,
SparseArray[
Automatic, {10, 10}, 0, {
1, {{0, 2, 5, 8, 11, 13, 14, 15, 16, 17, 18}, {{2}, {3}, {
1}, {4}, {5}, {1}, {6}, {7}, {2}, {8}, {9}, {2}, {10}, {
3}, {3}, {4}, {4}, {5}}}, Pattern}]}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{1.9280537607514543`, 2.4354363293702583`}, {1.0147651372376076`, 1.6236242195801722`}, {2.8413423842653014`, 1.6236242195801722`}, {0.405906054895043, 0.8118121097900863}, {1.623624219580172, 0.8118121097900863}, {2.4354363293702583`, 0.8118121097900863}, {3.247248439160344, 0.8118121097900863}, {0., 0.}, {0.811812109790086, 0.}, {
1.623624219580172, 0.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {1, 3}, {2, 4}, {2, 5}, {3, 6}, {3, 7}, {
4, 8}, {4, 9}, {5, 10}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.03198674214401906], DiskBox[2, 0.03198674214401906], DiskBox[3, 0.03198674214401906], DiskBox[4, 0.03198674214401906], DiskBox[5, 0.03198674214401906], DiskBox[6, 0.03198674214401906], DiskBox[7, 0.03198674214401906], DiskBox[8, 0.03198674214401906], DiskBox[9, 0.03198674214401906], DiskBox[10, 0.03198674214401906]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "c6e9b35f-c856-4808-a0cf-2f210ee3d879",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), All, 4, "Padded" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/59ae86717aad4c20.png)
|
| Out[6]= |
|
Find the numbers of neighbors starting from node 20:
| In[7]:= |
![ResourceFunction["GraphNeighborhoodVolumes"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64}, {Null,
SparseArray[
Automatic, {64, 64}, 0, {
1, {{0, 2, 5, 8, 11, 14, 17, 20, 22, 25, 29, 33, 37, 41, 45,
49, 52, 55, 59, 63, 67, 71, 75, 79, 82, 85, 89, 93, 97, 101, 105, 109, 112, 115, 119, 123, 127, 131, 135, 139, 142, 145, 149, 153, 157, 161, 165, 169, 172, 175, 179, 183, 187, 191, 195, 199, 202, 204, 207, 210, 213, 216, 219, 222, 224}, {{2}, {9}, {1}, {3}, {10}, {2}, {4}, {
11}, {3}, {5}, {12}, {4}, {6}, {13}, {5}, {7}, {14}, {
6}, {8}, {15}, {7}, {16}, {1}, {10}, {17}, {2}, {9}, {
11}, {18}, {3}, {10}, {12}, {19}, {4}, {11}, {13}, {20}, {
5}, {12}, {14}, {21}, {6}, {13}, {15}, {22}, {7}, {14}, {
16}, {23}, {8}, {15}, {24}, {9}, {18}, {25}, {10}, {17}, {
19}, {26}, {11}, {18}, {20}, {27}, {12}, {19}, {21}, {
28}, {13}, {20}, {22}, {29}, {14}, {21}, {23}, {30}, {
15}, {22}, {24}, {31}, {16}, {23}, {32}, {17}, {26}, {
33}, {18}, {25}, {27}, {34}, {19}, {26}, {28}, {35}, {
20}, {27}, {29}, {36}, {21}, {28}, {30}, {37}, {22}, {
29}, {31}, {38}, {23}, {30}, {32}, {39}, {24}, {31}, {
40}, {25}, {34}, {41}, {26}, {33}, {35}, {42}, {27}, {
34}, {36}, {43}, {28}, {35}, {37}, {44}, {29}, {36}, {
38}, {45}, {30}, {37}, {39}, {46}, {31}, {38}, {40}, {
47}, {32}, {39}, {48}, {33}, {42}, {49}, {34}, {41}, {
43}, {50}, {35}, {42}, {44}, {51}, {36}, {43}, {45}, {
52}, {37}, {44}, {46}, {53}, {38}, {45}, {47}, {54}, {
39}, {46}, {48}, {55}, {40}, {47}, {56}, {41}, {50}, {
57}, {42}, {49}, {51}, {58}, {43}, {50}, {52}, {59}, {
44}, {51}, {53}, {60}, {45}, {52}, {54}, {61}, {46}, {
53}, {55}, {62}, {47}, {54}, {56}, {63}, {48}, {55}, {
64}, {49}, {58}, {50}, {57}, {59}, {51}, {58}, {60}, {
52}, {59}, {61}, {53}, {60}, {62}, {54}, {61}, {63}, {
55}, {62}, {64}, {56}, {63}}}, Pattern}]}, {
GraphLayout -> {"GridEmbedding", "Dimension" -> {8, 8}}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJx10zsKQyEUhGFJZWlhYXEKs5K4hiwhkDpbv0vIC0n4UOEy/BdhmDnH8+1x
vZ9SSuP1vfV7jstaP9f+OMMFrnCDA+5j7ZPGWjNc4Ao3OODpby598kYLXOEG
Bzz97dFc+pSNVrjBAU9/52aP5tKnbrTBAXfuuTfO0V7Nqa8acOe/e+reOEd7
Nae+akd378I9dW+co72a8+f7BDiQON4=
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {1, 9}, {2, 3}, {2, 10}, {3, 4}, {3, 11}, {4, 5}, {4, 12}, {5, 6}, {5, 13}, {6, 7}, {6, 14}, {
7, 8}, {7, 15}, {8, 16}, {9, 10}, {9, 17}, {10, 11}, {10, 18}, {11, 12}, {11, 19}, {12, 13}, {12, 20}, {13, 14}, {
13, 21}, {14, 15}, {14, 22}, {15, 16}, {15, 23}, {16, 24}, {17, 18}, {17, 25}, {18, 19}, {18, 26}, {19, 20}, {
19, 27}, {20, 21}, {20, 28}, {21, 22}, {21, 29}, {22, 23}, {22, 30}, {23, 24}, {23, 31}, {24, 32}, {25, 26}, {
25, 33}, {26, 27}, {26, 34}, {27, 28}, {27, 35}, {28, 29}, {28, 36}, {29, 30}, {29, 37}, {30, 31}, {30, 38}, {
31, 32}, {31, 39}, {32, 40}, {33, 34}, {33, 41}, {34, 35}, {34, 42}, {35, 36}, {35, 43}, {36, 37}, {36, 44}, {
37, 38}, {37, 45}, {38, 39}, {38, 46}, {39, 40}, {39, 47}, {40, 48}, {41, 42}, {41, 49}, {42, 43}, {42, 50}, {
43, 44}, {43, 51}, {44, 45}, {44, 52}, {45, 46}, {45, 53}, {46, 47}, {46, 54}, {47, 48}, {47, 55}, {48, 56}, {
49, 50}, {49, 57}, {50, 51}, {50, 58}, {51, 52}, {51, 59}, {52, 53}, {52, 60}, {53, 54}, {53, 61}, {54, 55}, {
54, 62}, {55, 56}, {55, 63}, {56, 64}, {57, 58}, {58, 59}, {59, 60}, {60, 61}, {61, 62}, {62, 63}, {63, 64}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.05338164251207729], DiskBox[2, 0.05338164251207729], DiskBox[3, 0.05338164251207729], DiskBox[4, 0.05338164251207729], DiskBox[5, 0.05338164251207729], DiskBox[6, 0.05338164251207729], DiskBox[7, 0.05338164251207729], DiskBox[8, 0.05338164251207729], DiskBox[9, 0.05338164251207729], DiskBox[10, 0.05338164251207729], DiskBox[11, 0.05338164251207729], DiskBox[12, 0.05338164251207729], DiskBox[13, 0.05338164251207729], DiskBox[14, 0.05338164251207729], DiskBox[15, 0.05338164251207729], DiskBox[16, 0.05338164251207729], DiskBox[17, 0.05338164251207729], DiskBox[18, 0.05338164251207729], DiskBox[19, 0.05338164251207729], DiskBox[20, 0.05338164251207729], DiskBox[21, 0.05338164251207729], DiskBox[22, 0.05338164251207729], DiskBox[23, 0.05338164251207729], DiskBox[24, 0.05338164251207729], DiskBox[25, 0.05338164251207729], DiskBox[26, 0.05338164251207729], DiskBox[27, 0.05338164251207729], DiskBox[28, 0.05338164251207729], DiskBox[29, 0.05338164251207729], DiskBox[30, 0.05338164251207729], DiskBox[31, 0.05338164251207729], DiskBox[32, 0.05338164251207729], DiskBox[33, 0.05338164251207729], DiskBox[34, 0.05338164251207729], DiskBox[35, 0.05338164251207729], DiskBox[36, 0.05338164251207729], DiskBox[37, 0.05338164251207729], DiskBox[38, 0.05338164251207729], DiskBox[39, 0.05338164251207729], DiskBox[40, 0.05338164251207729], DiskBox[41, 0.05338164251207729], DiskBox[42, 0.05338164251207729], DiskBox[43, 0.05338164251207729], DiskBox[44, 0.05338164251207729], DiskBox[45, 0.05338164251207729], DiskBox[46, 0.05338164251207729], DiskBox[47, 0.05338164251207729], DiskBox[48, 0.05338164251207729], DiskBox[49, 0.05338164251207729], DiskBox[50, 0.05338164251207729], DiskBox[51, 0.05338164251207729], DiskBox[52, 0.05338164251207729], DiskBox[53, 0.05338164251207729], DiskBox[54, 0.05338164251207729], DiskBox[55, 0.05338164251207729], DiskBox[56, 0.05338164251207729], DiskBox[57, 0.05338164251207729], DiskBox[58, 0.05338164251207729], DiskBox[59, 0.05338164251207729], DiskBox[60, 0.05338164251207729], DiskBox[61, 0.05338164251207729], DiskBox[62, 0.05338164251207729], DiskBox[63, 0.05338164251207729], DiskBox[64, 0.05338164251207729]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "7a4aded1-1fbd-448f-8d42-bd0248660166",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{107.2890625, Automatic}]\), {20}]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/38e35875dbb68db4.png)
|
| Out[7]= |
|
Applications (3)
Find the average volumes of successively larger balls around every vertex:
| In[8]:= |
![Map[MeanAround, Transpose[Values[ResourceFunction["GraphNeighborhoodVolumes"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62,
63, 64}, {Null,
SparseArray[
Automatic, {64, 64}, 0, {
1, {{0, 2, 5, 8, 11, 14, 17, 20, 22, 25, 29, 33, 37, 41, 45, 49, 52, 55, 59, 63, 67, 71, 75, 79, 82, 85, 89, 93,
97, 101, 105, 109, 112, 115, 119, 123, 127, 131, 135, 139, 142, 145, 149, 153, 157, 161, 165, 169, 172, 175, 179, 183, 187, 191, 195, 199, 202, 204, 207, 210, 213, 216, 219, 222, 224}, {{2}, {9}, {1}, {3}, {10}, {2}, {
4}, {11}, {3}, {5}, {12}, {4}, {6}, {13}, {5}, {7}, {
14}, {6}, {8}, {15}, {7}, {16}, {1}, {10}, {17}, {2}, {
9}, {11}, {18}, {3}, {10}, {12}, {19}, {4}, {11}, {
13}, {20}, {5}, {12}, {14}, {21}, {6}, {13}, {15}, {
22}, {7}, {14}, {16}, {23}, {8}, {15}, {24}, {9}, {
18}, {25}, {10}, {17}, {19}, {26}, {11}, {18}, {20}, {
27}, {12}, {19}, {21}, {28}, {13}, {20}, {22}, {29}, {
14}, {21}, {23}, {30}, {15}, {22}, {24}, {31}, {16}, {
23}, {32}, {17}, {26}, {33}, {18}, {25}, {27}, {34}, {
19}, {26}, {28}, {35}, {20}, {27}, {29}, {36}, {21}, {
28}, {30}, {37}, {22}, {29}, {31}, {38}, {23}, {30}, {
32}, {39}, {24}, {31}, {40}, {25}, {34}, {41}, {26}, {
33}, {35}, {42}, {27}, {34}, {36}, {43}, {28}, {35}, {
37}, {44}, {29}, {36}, {38}, {45}, {30}, {37}, {39}, {
46}, {31}, {38}, {40}, {47}, {32}, {39}, {48}, {33}, {
42}, {49}, {34}, {41}, {43}, {50}, {35}, {42}, {44}, {
51}, {36}, {43}, {45}, {52}, {37}, {44}, {46}, {53}, {
38}, {45}, {47}, {54}, {39}, {46}, {48}, {55}, {40}, {
47}, {56}, {41}, {50}, {57}, {42}, {49}, {51}, {58}, {
43}, {50}, {52}, {59}, {44}, {51}, {53}, {60}, {45}, {
52}, {54}, {61}, {46}, {53}, {55}, {62}, {47}, {54}, {
56}, {63}, {48}, {55}, {64}, {49}, {58}, {50}, {57}, {
59}, {51}, {58}, {60}, {52}, {59}, {61}, {53}, {60}, {
62}, {54}, {61}, {63}, {55}, {62}, {64}, {56}, {63}}}, Pattern}]}, {
GraphLayout -> {
"GridEmbedding", "Dimension" -> {8, 8}}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJx10zsKQyEUhGFJZWlhYXEKs5K4hiwhkDpbv0vIC0n4UOEy/BdhmDnH8+1x
vZ9SSuP1vfV7jstaP9f+OMMFrnCDA+5j7ZPGWjNc4Ao3OODpby598kYLXOEG
Bzz97dFc+pSNVrjBAU9/52aP5tKnbrTBAXfuuTfO0V7Nqa8acOe/e+reOEd7
Nae+akd378I9dW+co72a8+f7BDiQON4=
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {1, 9}, {2, 3}, {2, 10}, {3, 4}, {3, 11}, {4, 5}, {4, 12}, {5, 6}, {5, 13}, {6, 7}, {6, 14}, {7, 8}, {7, 15}, {8, 16}, {9, 10}, {9, 17}, {10, 11}, {10, 18}, {11, 12}, {11, 19}, {12, 13}, {12, 20}, {13, 14}, {13, 21}, {14, 15}, {14, 22}, {15, 16}, {15, 23}, {16, 24}, {17, 18}, {17, 25}, {18, 19}, {18, 26}, {19, 20}, {19, 27}, {20, 21}, {20, 28}, {21, 22}, {21, 29}, {22, 23}, {22, 30}, {23, 24}, {23, 31}, {24, 32}, {25, 26}, {25, 33}, {26, 27}, {26, 34}, {27, 28}, {27, 35}, {28, 29}, {28, 36}, {29, 30}, {29, 37}, {30, 31}, {30, 38}, {31, 32}, {31, 39}, {32, 40}, {33, 34}, {33, 41}, {34, 35}, {34, 42}, {35, 36}, {35, 43}, {36, 37}, {36, 44}, {37, 38}, {37, 45}, {38, 39}, {38, 46}, {39, 40}, {39, 47}, {40, 48}, {41, 42}, {41, 49}, {42, 43}, {42, 50}, {43, 44}, {43, 51}, {44, 45}, {44, 52}, {45, 46}, {45, 53}, {46, 47}, {46, 54}, {47, 48}, {47, 55}, {48, 56}, {49, 50}, {49, 57}, {50, 51}, {50, 58}, {51, 52}, {51, 59}, {52, 53}, {52, 60}, {53, 54}, {53, 61}, {54, 55}, {54, 62}, {55, 56}, {55, 63}, {56, 64}, {57, 58}, {58, 59}, {59, 60}, {60, 61}, {61, 62}, {62, 63}, {63, 64}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.05338164251207729], DiskBox[2, 0.05338164251207729], DiskBox[3, 0.05338164251207729], DiskBox[4, 0.05338164251207729], DiskBox[5, 0.05338164251207729], DiskBox[6, 0.05338164251207729], DiskBox[7, 0.05338164251207729], DiskBox[8, 0.05338164251207729], DiskBox[9, 0.05338164251207729], DiskBox[10, 0.05338164251207729], DiskBox[11, 0.05338164251207729], DiskBox[12, 0.05338164251207729], DiskBox[13, 0.05338164251207729], DiskBox[14, 0.05338164251207729], DiskBox[15, 0.05338164251207729], DiskBox[16, 0.05338164251207729], DiskBox[17, 0.05338164251207729], DiskBox[18, 0.05338164251207729], DiskBox[19, 0.05338164251207729], DiskBox[20, 0.05338164251207729], DiskBox[21, 0.05338164251207729], DiskBox[22, 0.05338164251207729], DiskBox[23, 0.05338164251207729], DiskBox[24, 0.05338164251207729], DiskBox[25, 0.05338164251207729], DiskBox[26, 0.05338164251207729], DiskBox[27, 0.05338164251207729], DiskBox[28, 0.05338164251207729], DiskBox[29, 0.05338164251207729], DiskBox[30, 0.05338164251207729], DiskBox[31, 0.05338164251207729], DiskBox[32, 0.05338164251207729], DiskBox[33, 0.05338164251207729], DiskBox[34, 0.05338164251207729], DiskBox[35, 0.05338164251207729], DiskBox[36, 0.05338164251207729], DiskBox[37, 0.05338164251207729], DiskBox[38, 0.05338164251207729], DiskBox[39, 0.05338164251207729], DiskBox[40, 0.05338164251207729], DiskBox[41, 0.05338164251207729], DiskBox[42, 0.05338164251207729], DiskBox[43, 0.05338164251207729], DiskBox[44, 0.05338164251207729], DiskBox[45, 0.05338164251207729], DiskBox[46, 0.05338164251207729], DiskBox[47, 0.05338164251207729], DiskBox[48, 0.05338164251207729], DiskBox[49, 0.05338164251207729], DiskBox[50, 0.05338164251207729], DiskBox[51, 0.05338164251207729], DiskBox[52, 0.05338164251207729], DiskBox[53, 0.05338164251207729], DiskBox[54, 0.05338164251207729], DiskBox[55, 0.05338164251207729], DiskBox[56, 0.05338164251207729], DiskBox[57, 0.05338164251207729], DiskBox[58, 0.05338164251207729], DiskBox[59, 0.05338164251207729], DiskBox[60, 0.05338164251207729], DiskBox[61, 0.05338164251207729], DiskBox[62, 0.05338164251207729], DiskBox[63, 0.05338164251207729], DiskBox[64, 0.05338164251207729]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "cf7c41ff-b8bd-44df-8a98-3a799fed1fcc",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{107.2890625, Automatic}]\), All, Automatic]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/4d8bb78a9bcdf624.png)
|
| Out[8]= |
|
Plot the result:
| In[9]:= |
![ListLinePlot[%]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/1d2e1d7618d8e5ae.png){kind=small}
|
| Out[9]= |
|
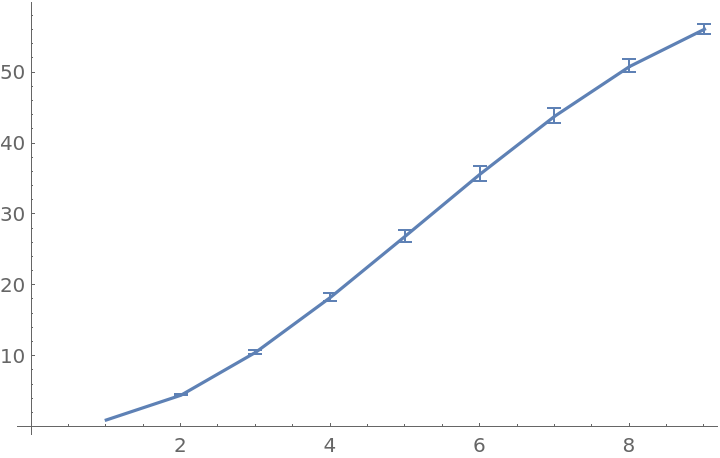
Find the average padded volumes of successively larger balls around every vertex:
| In[10]:= |
![Map[MeanAround, Transpose[Values[ResourceFunction["GraphNeighborhoodVolumes"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62,
63, 64}, {Null,
SparseArray[
Automatic, {64, 64}, 0, {
1, {{0, 2, 5, 8, 11, 14, 17, 20, 22, 25, 29, 33, 37, 41, 45, 49, 52, 55, 59, 63, 67, 71, 75, 79, 82, 85, 89, 93,
97, 101, 105, 109, 112, 115, 119, 123, 127, 131, 135, 139, 142, 145, 149, 153, 157, 161, 165, 169, 172, 175, 179, 183, 187, 191, 195, 199, 202, 204, 207, 210, 213, 216, 219, 222, 224}, {{2}, {9}, {1}, {3}, {10}, {2}, {
4}, {11}, {3}, {5}, {12}, {4}, {6}, {13}, {5}, {7}, {
14}, {6}, {8}, {15}, {7}, {16}, {1}, {10}, {17}, {2}, {
9}, {11}, {18}, {3}, {10}, {12}, {19}, {4}, {11}, {
13}, {20}, {5}, {12}, {14}, {21}, {6}, {13}, {15}, {
22}, {7}, {14}, {16}, {23}, {8}, {15}, {24}, {9}, {
18}, {25}, {10}, {17}, {19}, {26}, {11}, {18}, {20}, {
27}, {12}, {19}, {21}, {28}, {13}, {20}, {22}, {29}, {
14}, {21}, {23}, {30}, {15}, {22}, {24}, {31}, {16}, {
23}, {32}, {17}, {26}, {33}, {18}, {25}, {27}, {34}, {
19}, {26}, {28}, {35}, {20}, {27}, {29}, {36}, {21}, {
28}, {30}, {37}, {22}, {29}, {31}, {38}, {23}, {30}, {
32}, {39}, {24}, {31}, {40}, {25}, {34}, {41}, {26}, {
33}, {35}, {42}, {27}, {34}, {36}, {43}, {28}, {35}, {
37}, {44}, {29}, {36}, {38}, {45}, {30}, {37}, {39}, {
46}, {31}, {38}, {40}, {47}, {32}, {39}, {48}, {33}, {
42}, {49}, {34}, {41}, {43}, {50}, {35}, {42}, {44}, {
51}, {36}, {43}, {45}, {52}, {37}, {44}, {46}, {53}, {
38}, {45}, {47}, {54}, {39}, {46}, {48}, {55}, {40}, {
47}, {56}, {41}, {50}, {57}, {42}, {49}, {51}, {58}, {
43}, {50}, {52}, {59}, {44}, {51}, {53}, {60}, {45}, {
52}, {54}, {61}, {46}, {53}, {55}, {62}, {47}, {54}, {
56}, {63}, {48}, {55}, {64}, {49}, {58}, {50}, {57}, {
59}, {51}, {58}, {60}, {52}, {59}, {61}, {53}, {60}, {
62}, {54}, {61}, {63}, {55}, {62}, {64}, {56}, {63}}}, Pattern}]}, {
GraphLayout -> {
"GridEmbedding", "Dimension" -> {8, 8}}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJx10zsKQyEUhGFJZWlhYXEKs5K4hiwhkDpbv0vIC0n4UOEy/BdhmDnH8+1x
vZ9SSuP1vfV7jstaP9f+OMMFrnCDA+5j7ZPGWjNc4Ao3OODpby598kYLXOEG
Bzz97dFc+pSNVrjBAU9/52aP5tKnbrTBAXfuuTfO0V7Nqa8acOe/e+reOEd7
Nae+akd378I9dW+co72a8+f7BDiQON4=
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {1, 9}, {2, 3}, {2, 10}, {3, 4}, {3, 11}, {4, 5}, {4, 12}, {5, 6}, {5, 13}, {6, 7}, {6, 14}, {7, 8}, {7, 15}, {8, 16}, {9, 10}, {9, 17}, {10, 11}, {10, 18}, {11, 12}, {11, 19}, {12, 13}, {12, 20}, {13, 14}, {13, 21}, {14, 15}, {14, 22}, {15, 16}, {15, 23}, {16, 24}, {17, 18}, {17, 25}, {18, 19}, {18, 26}, {19, 20}, {19, 27}, {20, 21}, {20, 28}, {21, 22}, {21, 29}, {22, 23}, {22, 30}, {23, 24}, {23, 31}, {24, 32}, {25, 26}, {25, 33}, {26, 27}, {26, 34}, {27, 28}, {27, 35}, {28, 29}, {28, 36}, {29, 30}, {29, 37}, {30, 31}, {30, 38}, {31, 32}, {31, 39}, {32, 40}, {33, 34}, {33, 41}, {34, 35}, {34, 42}, {35, 36}, {35, 43}, {36, 37}, {36, 44}, {37, 38}, {37, 45}, {38, 39}, {38, 46}, {39, 40}, {39, 47}, {40, 48}, {41, 42}, {41, 49}, {42, 43}, {42, 50}, {43, 44}, {43, 51}, {44, 45}, {44, 52}, {45, 46}, {45, 53}, {46, 47}, {46, 54}, {47, 48}, {47, 55}, {48, 56}, {49, 50}, {49, 57}, {50, 51}, {50, 58}, {51, 52}, {51, 59}, {52, 53}, {52, 60}, {53, 54}, {53, 61}, {54, 55}, {54, 62}, {55, 56}, {55, 63}, {56, 64}, {57, 58}, {58, 59}, {59, 60}, {60, 61}, {61, 62}, {62, 63}, {63, 64}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.05338164251207729], DiskBox[2, 0.05338164251207729], DiskBox[3, 0.05338164251207729], DiskBox[4, 0.05338164251207729], DiskBox[5, 0.05338164251207729], DiskBox[6, 0.05338164251207729], DiskBox[7, 0.05338164251207729], DiskBox[8, 0.05338164251207729], DiskBox[9, 0.05338164251207729], DiskBox[10, 0.05338164251207729], DiskBox[11, 0.05338164251207729], DiskBox[12, 0.05338164251207729], DiskBox[13, 0.05338164251207729], DiskBox[14, 0.05338164251207729], DiskBox[15, 0.05338164251207729], DiskBox[16, 0.05338164251207729], DiskBox[17, 0.05338164251207729], DiskBox[18, 0.05338164251207729], DiskBox[19, 0.05338164251207729], DiskBox[20, 0.05338164251207729], DiskBox[21, 0.05338164251207729], DiskBox[22, 0.05338164251207729], DiskBox[23, 0.05338164251207729], DiskBox[24, 0.05338164251207729], DiskBox[25, 0.05338164251207729], DiskBox[26, 0.05338164251207729], DiskBox[27, 0.05338164251207729], DiskBox[28, 0.05338164251207729], DiskBox[29, 0.05338164251207729], DiskBox[30, 0.05338164251207729], DiskBox[31, 0.05338164251207729], DiskBox[32, 0.05338164251207729], DiskBox[33, 0.05338164251207729], DiskBox[34, 0.05338164251207729], DiskBox[35, 0.05338164251207729], DiskBox[36, 0.05338164251207729], DiskBox[37, 0.05338164251207729], DiskBox[38, 0.05338164251207729], DiskBox[39, 0.05338164251207729], DiskBox[40, 0.05338164251207729], DiskBox[41, 0.05338164251207729], DiskBox[42, 0.05338164251207729], DiskBox[43, 0.05338164251207729], DiskBox[44, 0.05338164251207729], DiskBox[45, 0.05338164251207729], DiskBox[46, 0.05338164251207729], DiskBox[47, 0.05338164251207729], DiskBox[48, 0.05338164251207729], DiskBox[49, 0.05338164251207729], DiskBox[50, 0.05338164251207729], DiskBox[51, 0.05338164251207729], DiskBox[52, 0.05338164251207729], DiskBox[53, 0.05338164251207729], DiskBox[54, 0.05338164251207729], DiskBox[55, 0.05338164251207729], DiskBox[56, 0.05338164251207729], DiskBox[57, 0.05338164251207729], DiskBox[58, 0.05338164251207729], DiskBox[59, 0.05338164251207729], DiskBox[60, 0.05338164251207729], DiskBox[61, 0.05338164251207729], DiskBox[62, 0.05338164251207729], DiskBox[63, 0.05338164251207729], DiskBox[64, 0.05338164251207729]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "cf7c41ff-b8bd-44df-8a98-3a799fed1fcc",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{107.2890625, Automatic}]\), All, "Padded" -> True]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/4d1ca7fb2b56a7a9.png)
|
| Out[10]= |
|
| In[11]:= |
![ListLinePlot[%]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/057e6c9ec985f923.png){kind=small}
|
| Out[11]= |
|
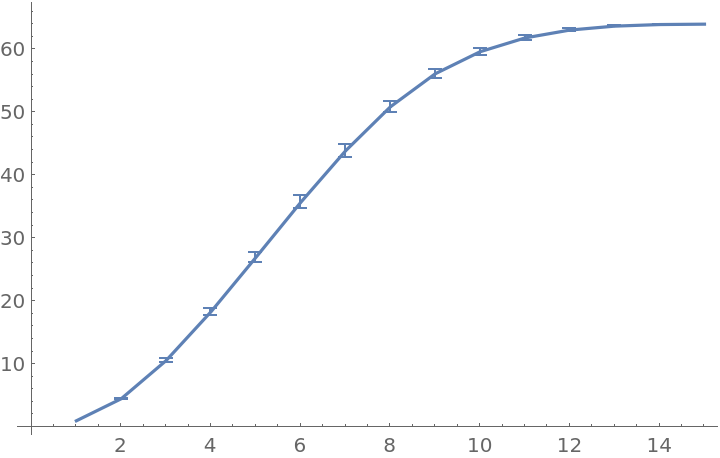
Converting the undirected graph from the previous example into a graph with asymmetric edges illustrates how padding helps:
| In[12]:= |
![Map[MeanAround, Transpose[
Values[ResourceFunction["GraphNeighborhoodVolumes"][
DirectedGraph[\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64}, {Null,
SparseArray[
Automatic, {64, 64}, 0, {
1, {{0, 2, 5, 8, 11, 14, 17, 20, 22, 25, 29, 33, 37, 41,
45, 49, 52, 55, 59, 63, 67, 71, 75, 79, 82, 85, 89, 93, 97, 101, 105, 109, 112, 115, 119, 123, 127, 131, 135, 139, 142, 145, 149, 153, 157, 161, 165, 169, 172,
175, 179, 183, 187, 191, 195, 199, 202, 204, 207, 210, 213, 216, 219, 222, 224}, {{2}, {9}, {1}, {3}, {
10}, {2}, {4}, {11}, {3}, {5}, {12}, {4}, {6}, {13}, {
5}, {7}, {14}, {6}, {8}, {15}, {7}, {16}, {1}, {10}, {
17}, {2}, {9}, {11}, {18}, {3}, {10}, {12}, {19}, {
4}, {11}, {13}, {20}, {5}, {12}, {14}, {21}, {6}, {
13}, {15}, {22}, {7}, {14}, {16}, {23}, {8}, {15}, {
24}, {9}, {18}, {25}, {10}, {17}, {19}, {26}, {11}, {
18}, {20}, {27}, {12}, {19}, {21}, {28}, {13}, {20}, {
22}, {29}, {14}, {21}, {23}, {30}, {15}, {22}, {24}, {
31}, {16}, {23}, {32}, {17}, {26}, {33}, {18}, {25}, {
27}, {34}, {19}, {26}, {28}, {35}, {20}, {27}, {29}, {
36}, {21}, {28}, {30}, {37}, {22}, {29}, {31}, {38}, {
23}, {30}, {32}, {39}, {24}, {31}, {40}, {25}, {34}, {
41}, {26}, {33}, {35}, {42}, {27}, {34}, {36}, {43}, {
28}, {35}, {37}, {44}, {29}, {36}, {38}, {45}, {30}, {
37}, {39}, {46}, {31}, {38}, {40}, {47}, {32}, {39}, {
48}, {33}, {42}, {49}, {34}, {41}, {43}, {50}, {35}, {
42}, {44}, {51}, {36}, {43}, {45}, {52}, {37}, {44}, {
46}, {53}, {38}, {45}, {47}, {54}, {39}, {46}, {48}, {
55}, {40}, {47}, {56}, {41}, {50}, {57}, {42}, {49}, {
51}, {58}, {43}, {50}, {52}, {59}, {44}, {51}, {53}, {
60}, {45}, {52}, {54}, {61}, {46}, {53}, {55}, {62}, {
47}, {54}, {56}, {63}, {48}, {55}, {64}, {49}, {58}, {
50}, {57}, {59}, {51}, {58}, {60}, {52}, {59}, {61}, {
53}, {60}, {62}, {54}, {61}, {63}, {55}, {62}, {64}, {
56}, {63}}}, Pattern}]}, {
GraphLayout -> {
"GridEmbedding", "Dimension" -> {8, 8}}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJx10zsKQyEUhGFJZWlhYXEKs5K4hiwhkDpbv0vIC0n4UOEy/BdhmDnH8+1x
vZ9SSuP1vfV7jstaP9f+OMMFrnCDA+5j7ZPGWjNc4Ao3OODpby598kYLXOEG
Bzz97dFc+pSNVrjBAU9/52aP5tKnbrTBAXfuuTfO0V7Nqa8acOe/e+reOEd7
Nae+akd378I9dW+co72a8+f7BDiQON4=
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {1, 9}, {2, 3}, {2, 10}, {3, 4}, {3, 11}, {4, 5}, {4, 12}, {5, 6}, {5, 13}, {6, 7}, {6, 14}, {7, 8}, {7, 15}, {8, 16}, {9, 10}, {9, 17}, {10, 11}, {10, 18}, {11, 12}, {11, 19}, {12, 13}, {12, 20}, {13, 14}, {13, 21}, {14, 15}, {14, 22}, {15, 16}, {15, 23}, {16, 24}, {17, 18}, {17, 25}, {18, 19}, {18, 26}, {19, 20}, {19, 27}, {20, 21}, {20, 28}, {21, 22}, {21, 29}, {22, 23}, {22, 30}, {23, 24}, {23, 31}, {24, 32}, {25, 26}, {25, 33}, {26, 27}, {26, 34}, {27, 28}, {27, 35}, {28, 29}, {28, 36}, {29, 30}, {29, 37}, {30, 31}, {30, 38}, {31, 32}, {31, 39}, {32, 40}, {33, 34}, {33, 41}, {34, 35}, {34, 42}, {35, 36}, {35, 43}, {36, 37}, {36, 44}, {37, 38}, {37, 45}, {38, 39}, {38, 46}, {39, 40}, {39, 47}, {40, 48}, {41, 42}, {41, 49}, {42, 43}, {42, 50}, {43, 44}, {43, 51}, {44, 45}, {44, 52}, {45, 46}, {45, 53}, {46, 47}, {46, 54}, {47, 48}, {47, 55}, {48, 56}, {49, 50}, {49, 57}, {50, 51}, {50, 58}, {51, 52}, {51, 59}, {52, 53}, {52, 60}, {53, 54}, {53, 61}, {54, 55}, {54, 62}, {55, 56}, {55, 63}, {56, 64}, {57, 58}, {58, 59}, {59, 60}, {60, 61}, {61, 62}, {62, 63}, {63, 64}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.05338164251207729], DiskBox[2, 0.05338164251207729], DiskBox[3, 0.05338164251207729], DiskBox[4, 0.05338164251207729], DiskBox[5, 0.05338164251207729], DiskBox[6, 0.05338164251207729], DiskBox[7, 0.05338164251207729], DiskBox[8, 0.05338164251207729], DiskBox[9, 0.05338164251207729], DiskBox[10, 0.05338164251207729], DiskBox[11, 0.05338164251207729], DiskBox[12, 0.05338164251207729], DiskBox[13, 0.05338164251207729], DiskBox[14, 0.05338164251207729], DiskBox[15, 0.05338164251207729], DiskBox[16, 0.05338164251207729], DiskBox[17, 0.05338164251207729], DiskBox[18, 0.05338164251207729], DiskBox[19, 0.05338164251207729], DiskBox[20, 0.05338164251207729], DiskBox[21, 0.05338164251207729], DiskBox[22, 0.05338164251207729], DiskBox[23, 0.05338164251207729], DiskBox[24, 0.05338164251207729], DiskBox[25, 0.05338164251207729], DiskBox[26, 0.05338164251207729], DiskBox[27, 0.05338164251207729], DiskBox[28, 0.05338164251207729], DiskBox[29, 0.05338164251207729], DiskBox[30, 0.05338164251207729], DiskBox[31, 0.05338164251207729], DiskBox[32, 0.05338164251207729], DiskBox[33, 0.05338164251207729], DiskBox[34, 0.05338164251207729], DiskBox[35, 0.05338164251207729], DiskBox[36, 0.05338164251207729], DiskBox[37, 0.05338164251207729], DiskBox[38, 0.05338164251207729], DiskBox[39, 0.05338164251207729], DiskBox[40, 0.05338164251207729], DiskBox[41, 0.05338164251207729], DiskBox[42, 0.05338164251207729], DiskBox[43, 0.05338164251207729], DiskBox[44, 0.05338164251207729], DiskBox[45, 0.05338164251207729], DiskBox[46, 0.05338164251207729], DiskBox[47, 0.05338164251207729], DiskBox[48, 0.05338164251207729], DiskBox[49, 0.05338164251207729], DiskBox[50, 0.05338164251207729], DiskBox[51, 0.05338164251207729], DiskBox[52, 0.05338164251207729], DiskBox[53, 0.05338164251207729], DiskBox[54, 0.05338164251207729], DiskBox[55, 0.05338164251207729], DiskBox[56, 0.05338164251207729], DiskBox[57, 0.05338164251207729], DiskBox[58, 0.05338164251207729], DiskBox[59, 0.05338164251207729], DiskBox[60, 0.05338164251207729], DiskBox[61, 0.05338164251207729], DiskBox[62, 0.05338164251207729], DiskBox[63, 0.05338164251207729], DiskBox[64, 0.05338164251207729]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "7a4aded1-1fbd-448f-8d42-bd0248660166",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{107.2890625, Automatic}]\), "Acyclic"], All, Automatic]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/3b2663c75f630578.png)
|
| Out[12]= |
|
Taking the padded graph neighborhood volumes bypasses the limitations in calculating volume that are imposed by vertices in directed graphs that have small radii:
| In[13]:= |
![Map[MeanAround, Transpose[
Values[ResourceFunction["GraphNeighborhoodVolumes"][
DirectedGraph[\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64}, {Null,
SparseArray[
Automatic, {64, 64}, 0, {
1, {{0, 2, 5, 8, 11, 14, 17, 20, 22, 25, 29, 33, 37, 41,
45, 49, 52, 55, 59, 63, 67, 71, 75, 79, 82, 85, 89, 93, 97, 101, 105, 109, 112, 115, 119, 123, 127, 131, 135, 139, 142, 145, 149, 153, 157, 161, 165, 169, 172,
175, 179, 183, 187, 191, 195, 199, 202, 204, 207, 210, 213, 216, 219, 222, 224}, {{2}, {9}, {1}, {3}, {
10}, {2}, {4}, {11}, {3}, {5}, {12}, {4}, {6}, {13}, {
5}, {7}, {14}, {6}, {8}, {15}, {7}, {16}, {1}, {10}, {
17}, {2}, {9}, {11}, {18}, {3}, {10}, {12}, {19}, {
4}, {11}, {13}, {20}, {5}, {12}, {14}, {21}, {6}, {
13}, {15}, {22}, {7}, {14}, {16}, {23}, {8}, {15}, {
24}, {9}, {18}, {25}, {10}, {17}, {19}, {26}, {11}, {
18}, {20}, {27}, {12}, {19}, {21}, {28}, {13}, {20}, {
22}, {29}, {14}, {21}, {23}, {30}, {15}, {22}, {24}, {
31}, {16}, {23}, {32}, {17}, {26}, {33}, {18}, {25}, {
27}, {34}, {19}, {26}, {28}, {35}, {20}, {27}, {29}, {
36}, {21}, {28}, {30}, {37}, {22}, {29}, {31}, {38}, {
23}, {30}, {32}, {39}, {24}, {31}, {40}, {25}, {34}, {
41}, {26}, {33}, {35}, {42}, {27}, {34}, {36}, {43}, {
28}, {35}, {37}, {44}, {29}, {36}, {38}, {45}, {30}, {
37}, {39}, {46}, {31}, {38}, {40}, {47}, {32}, {39}, {
48}, {33}, {42}, {49}, {34}, {41}, {43}, {50}, {35}, {
42}, {44}, {51}, {36}, {43}, {45}, {52}, {37}, {44}, {
46}, {53}, {38}, {45}, {47}, {54}, {39}, {46}, {48}, {
55}, {40}, {47}, {56}, {41}, {50}, {57}, {42}, {49}, {
51}, {58}, {43}, {50}, {52}, {59}, {44}, {51}, {53}, {
60}, {45}, {52}, {54}, {61}, {46}, {53}, {55}, {62}, {
47}, {54}, {56}, {63}, {48}, {55}, {64}, {49}, {58}, {
50}, {57}, {59}, {51}, {58}, {60}, {52}, {59}, {61}, {
53}, {60}, {62}, {54}, {61}, {63}, {55}, {62}, {64}, {
56}, {63}}}, Pattern}]}, {
GraphLayout -> {
"GridEmbedding", "Dimension" -> {8, 8}}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJx10zsKQyEUhGFJZWlhYXEKs5K4hiwhkDpbv0vIC0n4UOEy/BdhmDnH8+1x
vZ9SSuP1vfV7jstaP9f+OMMFrnCDA+5j7ZPGWjNc4Ao3OODpby598kYLXOEG
Bzz97dFc+pSNVrjBAU9/52aP5tKnbrTBAXfuuTfO0V7Nqa8acOe/e+reOEd7
Nae+akd378I9dW+co72a8+f7BDiQON4=
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {1, 9}, {2, 3}, {2, 10}, {3, 4}, {3, 11}, {4, 5}, {4, 12}, {5, 6}, {5, 13}, {6, 7}, {6, 14}, {7, 8}, {7, 15}, {8, 16}, {9, 10}, {9, 17}, {10, 11}, {10, 18}, {11, 12}, {11, 19}, {12, 13}, {12, 20}, {13, 14}, {13, 21}, {14, 15}, {14, 22}, {15, 16}, {15, 23}, {16, 24}, {17, 18}, {17, 25}, {18, 19}, {18, 26}, {19, 20}, {19, 27}, {20, 21}, {20, 28}, {21, 22}, {21, 29}, {22, 23}, {22, 30}, {23, 24}, {23, 31}, {24, 32}, {25, 26}, {25, 33}, {26, 27}, {26, 34}, {27, 28}, {27, 35}, {28, 29}, {28, 36}, {29, 30}, {29, 37}, {30, 31}, {30, 38}, {31, 32}, {31, 39}, {32, 40}, {33, 34}, {33, 41}, {34, 35}, {34, 42}, {35, 36}, {35, 43}, {36, 37}, {36, 44}, {37, 38}, {37, 45}, {38, 39}, {38, 46}, {39, 40}, {39, 47}, {40, 48}, {41, 42}, {41, 49}, {42, 43}, {42, 50}, {43, 44}, {43, 51}, {44, 45}, {44, 52}, {45, 46}, {45, 53}, {46, 47}, {46, 54}, {47, 48}, {47, 55}, {48, 56}, {49, 50}, {49, 57}, {50, 51}, {50, 58}, {51, 52}, {51, 59}, {52, 53}, {52, 60}, {53, 54}, {53, 61}, {54, 55}, {54, 62}, {55, 56}, {55, 63}, {56, 64}, {57, 58}, {58, 59}, {59, 60}, {60, 61}, {61, 62}, {62, 63}, {63, 64}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.05338164251207729], DiskBox[2, 0.05338164251207729], DiskBox[3, 0.05338164251207729], DiskBox[4, 0.05338164251207729], DiskBox[5, 0.05338164251207729], DiskBox[6, 0.05338164251207729], DiskBox[7, 0.05338164251207729], DiskBox[8, 0.05338164251207729], DiskBox[9, 0.05338164251207729], DiskBox[10, 0.05338164251207729], DiskBox[11, 0.05338164251207729], DiskBox[12, 0.05338164251207729], DiskBox[13, 0.05338164251207729], DiskBox[14, 0.05338164251207729], DiskBox[15, 0.05338164251207729], DiskBox[16, 0.05338164251207729], DiskBox[17, 0.05338164251207729], DiskBox[18, 0.05338164251207729], DiskBox[19, 0.05338164251207729], DiskBox[20, 0.05338164251207729], DiskBox[21, 0.05338164251207729], DiskBox[22, 0.05338164251207729], DiskBox[23, 0.05338164251207729], DiskBox[24, 0.05338164251207729], DiskBox[25, 0.05338164251207729], DiskBox[26, 0.05338164251207729], DiskBox[27, 0.05338164251207729], DiskBox[28, 0.05338164251207729], DiskBox[29, 0.05338164251207729], DiskBox[30, 0.05338164251207729], DiskBox[31, 0.05338164251207729], DiskBox[32, 0.05338164251207729], DiskBox[33, 0.05338164251207729], DiskBox[34, 0.05338164251207729], DiskBox[35, 0.05338164251207729], DiskBox[36, 0.05338164251207729], DiskBox[37, 0.05338164251207729], DiskBox[38, 0.05338164251207729], DiskBox[39, 0.05338164251207729], DiskBox[40, 0.05338164251207729], DiskBox[41, 0.05338164251207729], DiskBox[42, 0.05338164251207729], DiskBox[43, 0.05338164251207729], DiskBox[44, 0.05338164251207729], DiskBox[45, 0.05338164251207729], DiskBox[46, 0.05338164251207729], DiskBox[47, 0.05338164251207729], DiskBox[48, 0.05338164251207729], DiskBox[49, 0.05338164251207729], DiskBox[50, 0.05338164251207729], DiskBox[51, 0.05338164251207729], DiskBox[52, 0.05338164251207729], DiskBox[53, 0.05338164251207729], DiskBox[54, 0.05338164251207729], DiskBox[55, 0.05338164251207729], DiskBox[56, 0.05338164251207729], DiskBox[57, 0.05338164251207729], DiskBox[58, 0.05338164251207729], DiskBox[59, 0.05338164251207729], DiskBox[60, 0.05338164251207729], DiskBox[61, 0.05338164251207729], DiskBox[62, 0.05338164251207729], DiskBox[63, 0.05338164251207729], DiskBox[64, 0.05338164251207729]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "7a4aded1-1fbd-448f-8d42-bd0248660166",
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{107.2890625, Automatic}]\), "Acyclic"], All, "Padded" -> True]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/784b84833f871f84.png)
|
| Out[13]= |
|
| In[14]:= |
![ListLinePlot[%]](https://www.wolframcloud.com/obj/resourcesystem/images/bcc/bcce9306-a712-4235-b2dd-37419232cee7/0fc485752a5e7784.png){kind=small}
|
| Out[14]= |
|
Version History
- 3.0.0 – 15 October 2020
- 2.0.0 – 16 March 2020
- 1.0.0 – 04 December 2019
Related Symbols
License Information
This work is licensed under a Creative Commons Attribution 4.0 International License