Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Merge two graphs, linking them at a desired set of vertices
ResourceFunction["GraphMerge"][g1,g2,idx,v] merges two graphs g1 and g2, connecting them at the vertices listed in idx, and using the label v to label the vertices of g2. | |
ResourceFunction["GraphMerge"][g1,g2,dockingIndices] uses the string "v" as a label. |
Merge a Petersen graph and a complete graph at three of their vertices:
| In[1]:= |
| Out[1]= | 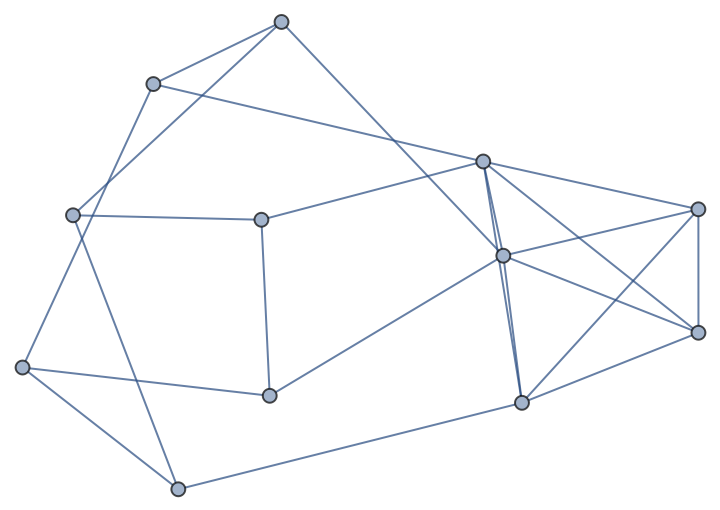 |
Display the vertex labels:
| In[2]:= |
| Out[2]= | 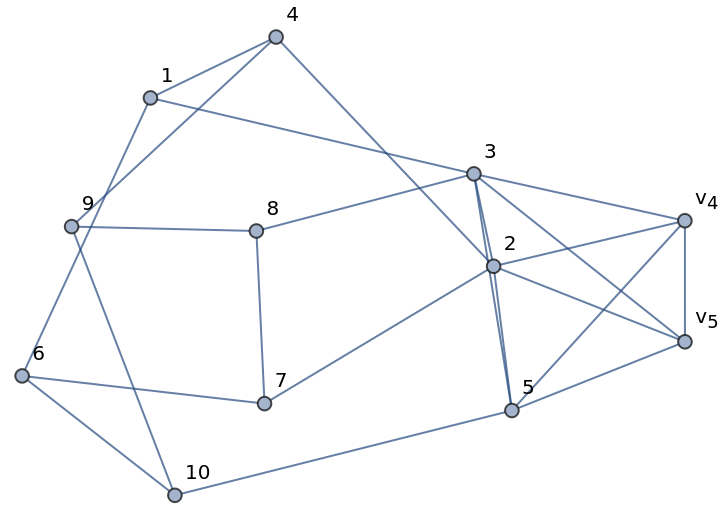 |
Merge two grid graphs of different sizes:
| In[3]:= |
| Out[3]= | 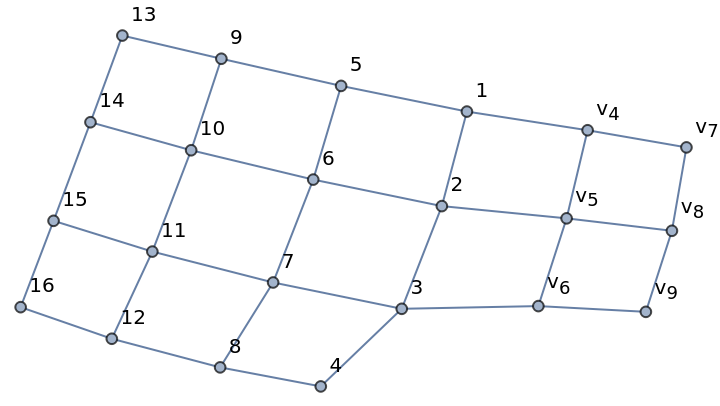 |
Merge two grid graphs of different dimensions:
| In[4]:= |
| Out[4]= | 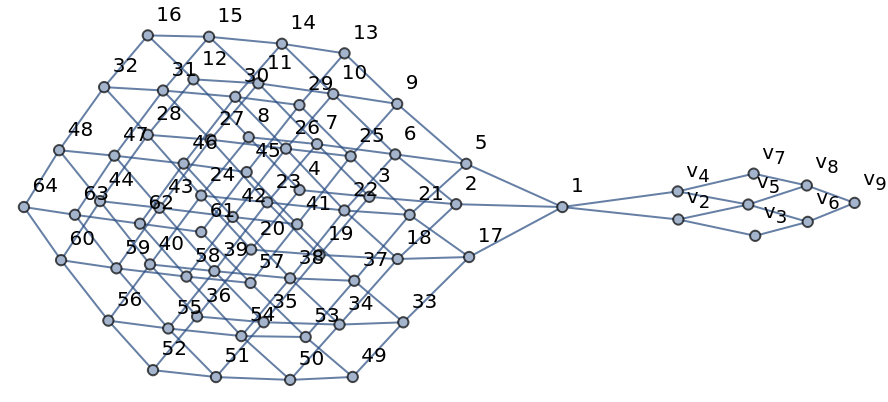 |
Merge a directed and an undirected graph:
| In[5]:= | ![Graph[ResourceFunction["GraphMerge"][ Graph[{1 \[DirectedEdge] 2, 2 \[DirectedEdge] 3, 3 \[DirectedEdge] 1}], GridGraph[{2, 2}], {1}, "b"], VertexLabels -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/655/6558dfbd-82e1-49d3-b2d5-9807aa26e803/58c56af3a84ef8a6.png) |
| Out[5]= | 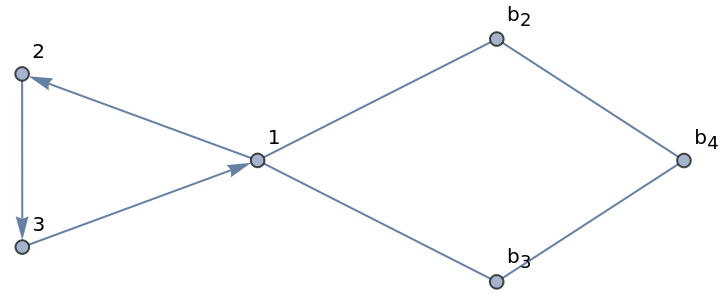 |
A grid graph:
| In[6]:= |
| Out[6]= |  |
Iteratively merge copies of the grid graph:
| In[7]:= |
| Out[7]= | 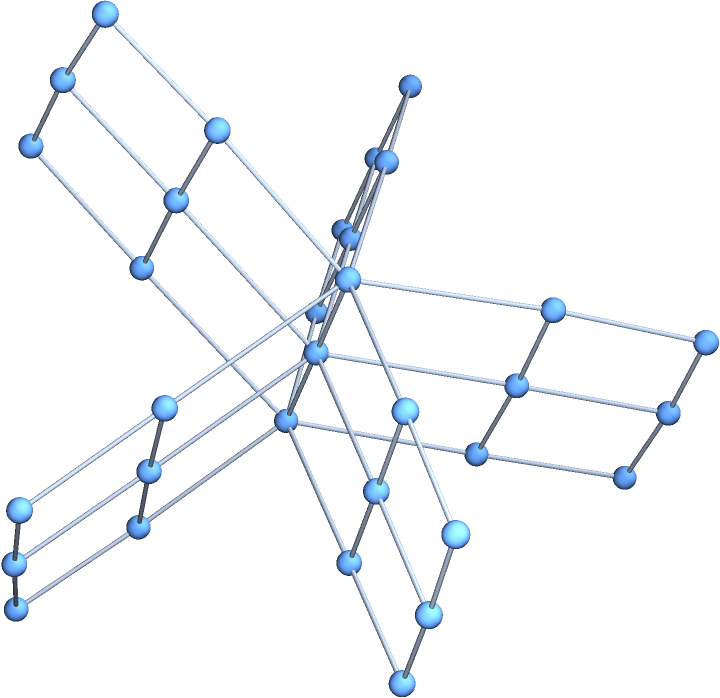 |
GraphMerge does not preserve the spatial appearance of the component graphs:
| In[8]:= | ![ResourceFunction["GraphMerge"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9}, {Null,
SparseArray[
Automatic, {9, 9}, 0, {1, {{0, 2, 5, 7, 10, 14, 17, 19, 22, 24}, {{2}, {4}, {
1}, {3}, {5}, {2}, {6}, {1}, {5}, {7}, {2}, {4}, {6}, {
8}, {3}, {5}, {9}, {4}, {8}, {5}, {7}, {9}, {6}, {8}}}, Pattern}]}, {GraphLayout -> {"GridEmbedding", "Dimension" -> {3, 3}}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[CompressedData["
1:eJxTTMoPSmVmYGDgAWImKIaAD/bYaQYHysQ5HLDLo9Po6mHi6HxSzSGkHt18
YsVx0cT6A6EPANxRGz8=
"], 0.02261146496815286]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{1., 1.}, 0.02261146496815286], InsetBox["1", Offset[{2, 2}, {1.0226114649681528, 1.0226114649681528}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.02261146496815286], InsetBox["2", Offset[{2, 2}, {1.0226114649681528, 2.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.02261146496815286], InsetBox["3", Offset[{2, 2}, {1.0226114649681528, 3.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{2., 1.}, 0.02261146496815286], InsetBox["4", Offset[{2, 2}, {2.022611464968153, 1.0226114649681528}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{2., 2.}, 0.02261146496815286], InsetBox["5", Offset[{2, 2}, {2.022611464968153, 2.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{2., 3.}, 0.02261146496815286], InsetBox["6", Offset[{2, 2}, {2.022611464968153, 3.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{3., 1.}, 0.02261146496815286], InsetBox["7", Offset[{2, 2}, {3.022611464968153, 1.0226114649681528}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{3., 2.}, 0.02261146496815286], InsetBox["8", Offset[{2, 2}, {3.022611464968153, 2.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{3., 3.}, 0.02261146496815286], InsetBox["9", Offset[{2, 2}, {3.022611464968153, 3.022611464968153}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), \!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27}, {Null,
SparseArray[
Automatic, {27, 27}, 0, {1, {{0, 3, 7, 10, 14, 19, 23, 26, 30, 33, 37, 42, 46, 51, 57, 62, 66, 71, 75, 78, 82, 85, 89, 94, 98, 101, 105, 108}, {{2}, {4}, {10}, {1}, {3}, {5}, {11}, {2}, {6}, {
12}, {1}, {5}, {7}, {13}, {2}, {4}, {6}, {8}, {14}, {3}, {
5}, {9}, {15}, {4}, {8}, {16}, {5}, {7}, {9}, {17}, {6}, {
8}, {18}, {1}, {11}, {13}, {19}, {2}, {10}, {12}, {14}, {
20}, {3}, {11}, {15}, {21}, {4}, {10}, {14}, {16}, {22}, {
5}, {11}, {13}, {15}, {17}, {23}, {6}, {12}, {14}, {18}, {
24}, {7}, {13}, {17}, {25}, {8}, {14}, {16}, {18}, {26}, {
9}, {15}, {17}, {27}, {10}, {20}, {22}, {11}, {19}, {
21}, {23}, {12}, {20}, {24}, {13}, {19}, {23}, {25}, {
14}, {20}, {22}, {24}, {26}, {15}, {21}, {23}, {27}, {
16}, {22}, {26}, {17}, {23}, {25}, {27}, {18}, {24}, {
26}}}, Pattern}]}, {GraphLayout -> {"Dimension" -> 3, "VertexLayout" -> "SpringElectricalEmbedding"}}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJwBmQJm/SFib1JlAgAAABsAAAADAAAAZl4R/A+c5T/NzGDTowj9PwAAAAAA
AAAAO7pYA3y/7D+/GrzH9E/sP1SpN0okptE/FF1ZHGuR8j8AAAAAAAAAAH20
DIvlW+Q/6QQTJPlE+T8Q8BkReCgBQJjzg854Tsw/sBPBOlFd/T+knLWwIFHz
P2byWl/Tx+A/3sfCb4iIAEDAC7eFne7SP9UTYcykz+w/hressT62A0ASyMpi
GnsDQF15UIEys+A/Tu296yHPBUC7uvHWuOD4P/FrzmaVWuo/Iv6SXCZ3B0Dk
M8GNy2DlP5+tWrBytPI/qM+pno/80j8H1P0QM1wAQAbLKsRmvOs/z2PANGdX
4D/9rbuf6cvxP1rYp91u9PI/MPJTSgyh6D+Af/UNkMzIP8a/wRmnXPg/bgHi
Zd1i8z9nLYBl5zoDQASOf5N79fE/GLw6D5BN9z+HwDVCA0b3P+Se50eiW/c/
gIAOWXtd+z/MmEer1wLgP7ig3MFS/Pw/2rQruXoJAUAYHiMW0bMFQBzRJOh0
TvY/G0Wkr2wmA0DGZVmdV/r8P4T+8gemnfs/ZsZOmdjrBEC26vJu9SrsP2/m
xGfqcABAAAAAAAAAAAAaYeyNwCECQERK1oGBV/w/UGDSsX6oxz8xrz8TJPb1
PxYSAioP2ABAYG6O0KbV2z9YlztLrZ3eP5FERM04PANALVRdSWcJ7D+85S/8
p+oEQIiqZUleTQBAUXw1fJOM8T8KOIowPFr7P5x7GAYgOgNASqwKIOh49T+I
CXgCE3foP9d5Rl3crAVAUvD3oE5O/D+oSgUHqTIHQLKrWXvxQAJACAK0eYgy
AEBwZhX+3UUAQOzRNyccEwVAKTx2AeLxAUCtTsM2HOLxP63DM9ElVwdAJ3Yr
Ow==
"], {
{Hue[0.6, 0.2, 0.8], Arrowheads[0.], Arrow3DBox[TubeBox[{{1, 2}, {1, 4}, {1, 10}, {2, 3}, {2, 5}, {2, 11}, {3, 6}, {3, 12}, {4, 5}, {4, 7}, {4, 13}, {5,
6}, {5, 8}, {5, 14}, {6, 9}, {6, 15}, {7, 8}, {7, 16}, {
8, 9}, {8, 17}, {9, 18}, {10, 11}, {10, 13}, {10, 19}, {
11, 12}, {11, 14}, {11, 20}, {12, 15}, {12, 21}, {13, 14}, {13, 16}, {13, 22}, {14, 15}, {14, 17}, {14, 23}, {
15, 18}, {15, 24}, {16, 17}, {16, 25}, {17, 18}, {17, 26}, {18, 27}, {19, 20}, {19, 22}, {20, 21}, {20, 23}, {
21, 24}, {22, 23}, {22, 25}, {23, 24}, {23, 26}, {24, 27}, {25, 26}, {26, 27}}], 0.05951680150138672]},
{Hue[0.6, 0.6, 1], SphereBox[1, 0.05951680150138672], SphereBox[2, 0.05951680150138672], SphereBox[3, 0.05951680150138672], SphereBox[4, 0.05951680150138672], SphereBox[5, 0.05951680150138672], SphereBox[6, 0.05951680150138672], SphereBox[7, 0.05951680150138672], SphereBox[8, 0.05951680150138672], SphereBox[9, 0.05951680150138672], SphereBox[10, 0.05951680150138672], SphereBox[11, 0.05951680150138672], SphereBox[12, 0.05951680150138672], SphereBox[13, 0.05951680150138672], SphereBox[14, 0.05951680150138672], SphereBox[15, 0.05951680150138672], SphereBox[16, 0.05951680150138672], SphereBox[17, 0.05951680150138672], SphereBox[18, 0.05951680150138672], SphereBox[19, 0.05951680150138672], SphereBox[20, 0.05951680150138672], SphereBox[21, 0.05951680150138672], SphereBox[22, 0.05951680150138672], SphereBox[23, 0.05951680150138672], SphereBox[24, 0.05951680150138672], SphereBox[25, 0.05951680150138672], SphereBox[26, 0.05951680150138672], SphereBox[27, 0.05951680150138672]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
BaseStyle->{Graphics3DBoxOptions -> {Method -> {"ShrinkWrap" -> True}}},
Boxed->False,
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}}]\), {5}]](https://www.wolframcloud.com/obj/resourcesystem/images/655/6558dfbd-82e1-49d3-b2d5-9807aa26e803/2e1562b1717682ef.png) |
| Out[8]= | 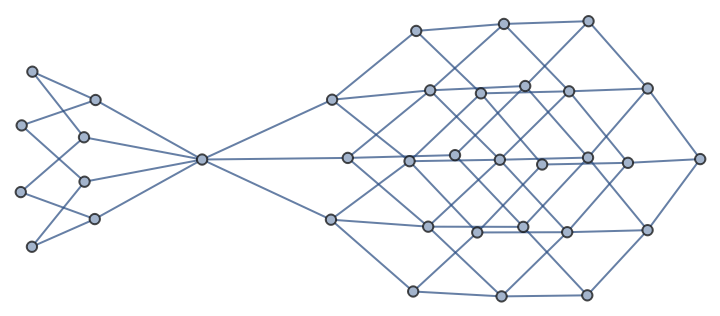 |
This work is licensed under a Creative Commons Attribution 4.0 International License