Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Graph
List the isolates in a graph
Contributed by:
Alejandra Ortiz Duran
ResourceFunction["GraphIsolates"][g] finds the isolates in the graph g. |
Details
GraphIsolates are nodes with no neighbors (nodes that have degree zero).
For directed graphs, this means no in-neighbors and no out-neighbors.
GraphIsolates returns a list of vertices.
GraphIsolates works with undirected graphs, directed graphs, weighted graphs, multigraphs and mixed graphs.
Examples
Basic Examples (2)
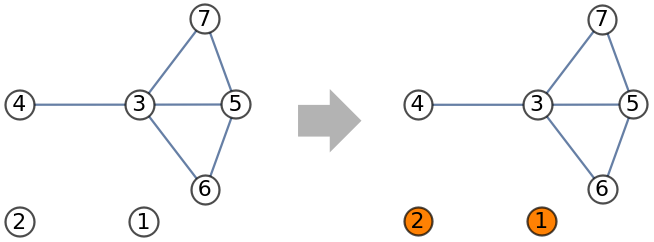
Find the isolates in a graph:
| In[1]:= | ![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7}, {Null, {{3, 4}, {3, 5}, {3, 6}, {3, 7}, {5, 6}, {5, 7}}}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {
Placed[Automatic, Center]}, VertexSize -> {0.4}, VertexStyle -> {
GrayLevel[1]}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{{1.3269318442955593`, -0.9892437663991506}, {
0.15707686886592276`, -0.9897810092789342}}, {{
1.3269318442955593`, -0.9892437663991506}, {
2.263562980639106, -0.9875219003939153}}, {{
1.3269318442955593`, -0.9892437663991506}, {
1.9632709963949249`, -1.8201956098748904`}}, {{
1.3269318442955593`, -0.9892437663991506}, {
1.9602463427453454`, -0.15707686886592298`}}, {{
2.263562980639106, -0.9875219003939153}, {
1.9632709963949249`, -1.8201956098748904`}}, {{
2.263562980639106, -0.9875219003939153}, {
1.9602463427453454`, -0.15707686886592298`}}}, 0.13472321796415104`]},
{GrayLevel[1], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{1.3673967936184375`, -2.134349347606736}, 0.13472321796415104], InsetBox["1", {1.3673967936184375, -2.134349347606736},
BaseStyle->"Graphics"]}, {
DiskBox[{0.15707686886592295`, -2.134349347606736}, 0.13472321796415104], InsetBox["2", {0.15707686886592295, -2.134349347606736},
BaseStyle->"Graphics"]}, {
DiskBox[{1.3269318442955593`, -0.9892437663991506}, 0.13472321796415104], InsetBox["3", {1.3269318442955593, -0.9892437663991506},
BaseStyle->"Graphics"]}, {
DiskBox[{0.15707686886592276`, -0.9897810092789342}, 0.13472321796415104], InsetBox["4", {0.15707686886592276, -0.9897810092789342},
BaseStyle->"Graphics"]}, {
DiskBox[{2.263562980639106, -0.9875219003939153}, 0.13472321796415104], InsetBox["5", {2.263562980639106, -0.9875219003939153},
BaseStyle->"Graphics"]}, {
DiskBox[{1.9632709963949249`, -1.8201956098748904`}, 0.13472321796415104], InsetBox["6", {1.9632709963949249, -1.8201956098748904},
BaseStyle->"Graphics"]}, {
DiskBox[{1.9602463427453454`, -0.15707686886592298`}, 0.13472321796415104], InsetBox["7", {1.9602463427453454, -0.15707686886592298},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{131.40000000000003`, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/4bc30274236d00b8.png) |
| In[2]:= | ![ResourceFunction["GraphIsolates"][g]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/696f7f7b8ad75342.png){kind=small} |
| Out[2]= |  |
Show the isolates:
| In[3]:= | ![HighlightGraph[g, Style[Subgraph[g, %], Orange]]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/5f7a3223438b3e90.png){kind=small} |
| Out[3]= |  |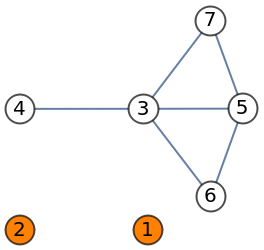
Find the isolates in a graph:
| In[4]:= | ![g = ResourceData["MathGroup Emails Network"]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/03d797bfc1acda73.png){kind=small} |
| Out[4]= |  |
| In[5]:= | ![ResourceFunction["GraphIsolates"][g]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/5dd1ba52bcf9d5b0.png){kind=small} |
| Out[5]= |  |
Show the isolates:
| In[6]:= | ![HighlightGraph[g, Style[Subgraph[g, %], Orange]]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/3564e5fff62f78a5.png){kind=small} |
| Out[6]= |  |
Scope (5)
Works with undirected graphs:
| In[7]:= | ![ResourceFunction["GraphIsolates"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7}, {Null, {{3, 4}, {3, 5}, {3, 6}, {3, 7}, {5, 6}, {5, 7}}}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {
Placed[Automatic, Center]}, VertexSize -> {0.4}, VertexStyle -> {
GrayLevel[1]}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{{1.3269318442955593`, -0.9892437663991506}, {
0.15707686886592276`, -0.9897810092789342}}, {{
1.3269318442955593`, -0.9892437663991506}, {
2.263562980639106, -0.9875219003939153}}, {{
1.3269318442955593`, -0.9892437663991506}, {
1.9632709963949249`, -1.8201956098748904`}}, {{
1.3269318442955593`, -0.9892437663991506}, {
1.9602463427453454`, -0.15707686886592298`}}, {{
2.263562980639106, -0.9875219003939153}, {
1.9632709963949249`, -1.8201956098748904`}}, {{
2.263562980639106, -0.9875219003939153}, {
1.9602463427453454`, -0.15707686886592298`}}}, 0.13472321796415104`]},
{GrayLevel[1], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{1.3673967936184375`, -2.134349347606736}, 0.13472321796415104], InsetBox["1", {1.3673967936184375, -2.134349347606736},
BaseStyle->"Graphics"]}, {
DiskBox[{0.15707686886592295`, -2.134349347606736}, 0.13472321796415104], InsetBox["2", {0.15707686886592295, -2.134349347606736},
BaseStyle->"Graphics"]}, {
DiskBox[{1.3269318442955593`, -0.9892437663991506}, 0.13472321796415104], InsetBox["3", {1.3269318442955593, -0.9892437663991506},
BaseStyle->"Graphics"]}, {
DiskBox[{0.15707686886592276`, -0.9897810092789342}, 0.13472321796415104], InsetBox["4", {0.15707686886592276, -0.9897810092789342},
BaseStyle->"Graphics"]}, {
DiskBox[{2.263562980639106, -0.9875219003939153}, 0.13472321796415104], InsetBox["5", {2.263562980639106, -0.9875219003939153},
BaseStyle->"Graphics"]}, {
DiskBox[{1.9632709963949249`, -1.8201956098748904`}, 0.13472321796415104], InsetBox["6", {1.9632709963949249, -1.8201956098748904},
BaseStyle->"Graphics"]}, {
DiskBox[{1.9602463427453454`, -0.15707686886592298`}, 0.13472321796415104], InsetBox["7", {1.9602463427453454, -0.15707686886592298},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{101.40000000000003`, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/6e4322d69eea12c4.png) |
| Out[7]= |  |
Directed graphs:
| In[8]:= | ![ResourceFunction["GraphIsolates"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7}, {{{3, 4}, {3, 5}, {4, 3}, {5, 6}, {7, 3}, {7, 6}}, Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {
Placed[Automatic, Center]}, VertexSize -> {0.4}, VertexStyle -> {
GrayLevel[1]}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[
BezierCurveBox[{{
1.2107001789863239`, -0.7160031191320814}, {
0.6836498360954942, -0.8894405470767316}, {
0.15653994499017188`, -0.7161841819632662}}], 0.1074346745267135], ArrowBox[{{1.2107001789863239`, -0.7160031191320814}, {
2.0684181690235244`, -0.15653994499017165`}}, 0.1074346745267135], ArrowBox[
BezierCurveBox[{{
0.15653994499017188`, -0.7161841819632662}, {
0.6835902878809974, -0.5427467540186182}, {
1.2107001789863239`, -0.7160031191320814}}], 0.1074346745267135], ArrowBox[{{2.0684181690235244`, -0.15653994499017165`}, {
2.7946034787257745`, -0.7162430396359889}}, 0.1074346745267135], ArrowBox[{{2.0686161983553526`, -1.2751950910186902`}, {
1.2107001789863239`, -0.7160031191320814}}, 0.1074346745267135], ArrowBox[{{2.0686161983553526`, -1.2751950910186902`}, {
2.7946034787257745`, -0.7162430396359889}}, 0.1074346745267135]},
{GrayLevel[1], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{1.6321116568481449`, -1.5882749809990335`}, 0.1074346745267135], InsetBox["1", {1.6321116568481449, -1.5882749809990335},
BaseStyle->"Graphics"]}, {
DiskBox[{0.15653994499017174`, -1.5882749809990335`}, 0.1074346745267135], InsetBox["2", {0.15653994499017174, -1.5882749809990335},
BaseStyle->"Graphics"]}, {
DiskBox[{1.2107001789863239`, -0.7160031191320814}, 0.1074346745267135], InsetBox["3", {1.2107001789863239, -0.7160031191320814},
BaseStyle->"Graphics"]}, {
DiskBox[{0.15653994499017188`, -0.7161841819632662}, 0.1074346745267135], InsetBox["4", {0.15653994499017188, -0.7161841819632662},
BaseStyle->"Graphics"]}, {
DiskBox[{2.0684181690235244`, -0.15653994499017165`}, 0.1074346745267135], InsetBox["5", {2.0684181690235244, -0.15653994499017165},
BaseStyle->"Graphics"]}, {
DiskBox[{2.7946034787257745`, -0.7162430396359889}, 0.1074346745267135], InsetBox["6", {2.7946034787257745, -0.7162430396359889},
BaseStyle->"Graphics"]}, {
DiskBox[{2.0686161983553526`, -1.2751950910186902`}, 0.1074346745267135], InsetBox["7", {2.0686161983553526, -1.2751950910186902},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{136.2000000000001, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/0fa0be5bfb5a23ab.png) |
| Out[8]= |  |
Weighted graphs:
| In[9]:= | ![ResourceFunction["GraphIsolates"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7}, {Null, {{3, 5}, {3, 6}, {3, 7}, {4, 6}, {5, 6}, {6, 7}}}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {
Placed[Automatic, Center]}, VertexSize -> {0.4}, VertexStyle -> {
GrayLevel[1]}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{{0.1570633317386938, -0.9883131811662736}, {
0.458779195641038, -1.8205290145769089`}}, {{
0.1570633317386938, -0.9883131811662736}, {
1.0938715434094206`, -0.9889357143765335}}, {{
0.1570633317386938, -0.9883131811662736}, {
0.4588593383911539, -0.15706333173869402`}}, {{
2.2628776106291335`, -0.9885676954501115}, {
1.0938715434094206`, -0.9889357143765335}}, {{
0.458779195641038, -1.8205290145769089`}, {
1.0938715434094206`, -0.9889357143765335}}, {{
1.0938715434094206`, -0.9889357143765335}, {
0.4588593383911539, -0.15706333173869402`}}}, 0.08711096905390822]},
{GrayLevel[1], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{1.3670338029226077`, -2.1346556780542967`}, 0.08711096905390822], InsetBox["1", {1.3670338029226077, -2.1346556780542967},
BaseStyle->"Graphics"]}, {
DiskBox[{0.15706333173869394`, -2.1346556780542967`}, 0.08711096905390822], InsetBox["2", {0.15706333173869394, -2.1346556780542967},
BaseStyle->"Graphics"]}, {
DiskBox[{0.1570633317386938, -0.9883131811662736}, 0.08711096905390822], InsetBox["3", {0.1570633317386938, -0.9883131811662736},
BaseStyle->"Graphics"]}, {
DiskBox[{2.2628776106291335`, -0.9885676954501115}, 0.08711096905390822], InsetBox["4", {2.2628776106291335, -0.9885676954501115},
BaseStyle->"Graphics"]}, {
DiskBox[{0.458779195641038, -1.8205290145769089`}, 0.08711096905390822], InsetBox["5", {0.458779195641038, -1.8205290145769089},
BaseStyle->"Graphics"]}, {
DiskBox[{1.0938715434094206`, -0.9889357143765335}, 0.08711096905390822], InsetBox["6", {1.0938715434094206, -0.9889357143765335},
BaseStyle->"Graphics"]}, {
DiskBox[{0.4588593383911539, -0.15706333173869402`}, 0.08711096905390822], InsetBox["7", {0.4588593383911539, -0.15706333173869402},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{147.00000000000034`, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/477a4678a68ab831.png) |
| Out[9]= |  |
Multigraphs:
| In[10]:= | ![ResourceFunction["GraphIsolates"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7}, {Null, {{3, 6}, {3, 7}, {4, 6}, {5, 6}, {6, 7}, {6, 3}}}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {
Placed[Automatic, Center]}, VertexSize -> {0.4}, VertexStyle -> {
GrayLevel[1]}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[
BezierCurveBox[{{
0.13744599986006023`, -0.5672797027666034}, {
0.6704371740937629, -0.598798393907716}, {
1.0806741032749794`, -0.9405273532281533}}], 0.1412291574356543], ArrowBox[
BezierCurveBox[{{
0.13744599986006023`, -0.5672797027666034}, {
0.5476829290412765, -0.9090086620870383}, {
1.0806741032749794`, -0.9405273532281533}}], 0.1412291574356543], ArrowBox[{{0.13744599986006023`, -0.5672797027666034}, {
0.1371362014409525, -1.3145201062665326`}}, 0.1412291574356543], ArrowBox[{{1.8173271977349363`, -1.7463934905628993`}, {
1.0806741032749794`, -0.9405273532281533}}, 0.1412291574356543], ArrowBox[{{1.818907746901864, -0.1371362014409525}, {
1.0806741032749794`, -0.9405273532281533}}, 0.1412291574356543], ArrowBox[{{1.0806741032749794`, -0.9405273532281533}, {
0.1371362014409525, -1.3145201062665326`}}, 0.1412291574356543]},
{GrayLevel[1], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{1.1151581756123607`, -2.020665893444804}, 0.1412291574356543], InsetBox["1", {1.1151581756123607, -2.020665893444804},
BaseStyle->"Graphics"]}, {
DiskBox[{0.13713620144095243`, -2.020665893444804}, 0.1412291574356543], InsetBox["2", {0.13713620144095243, -2.020665893444804},
BaseStyle->"Graphics"]}, {
DiskBox[{0.13744599986006023`, -0.5672797027666034}, 0.1412291574356543], InsetBox["3", {0.13744599986006023, -0.5672797027666034},
BaseStyle->"Graphics"]}, {
DiskBox[{1.8173271977349363`, -1.7463934905628993`}, 0.1412291574356543], InsetBox["4", {1.8173271977349363, -1.7463934905628993},
BaseStyle->"Graphics"]}, {
DiskBox[{1.818907746901864, -0.1371362014409525}, 0.1412291574356543], InsetBox["5", {1.818907746901864, -0.1371362014409525},
BaseStyle->"Graphics"]}, {
DiskBox[{1.0806741032749794`, -0.9405273532281533}, 0.1412291574356543], InsetBox["6", {1.0806741032749794, -0.9405273532281533},
BaseStyle->"Graphics"]}, {
DiskBox[{0.1371362014409525, -1.3145201062665326`}, 0.1412291574356543], InsetBox["7", {0.1371362014409525, -1.3145201062665326},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{92.66666666666674, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/3a4565db87a93ac4.png) |
| Out[10]= |  |
Mixed graphs:
| In[11]:= | ![ResourceFunction["GraphIsolates"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {{{3, 4}, {3, 5}, {4, 6}, {7, 5}}, {{6, 7}, {6, 8}, {7, 8}}}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {
Placed[Automatic, Center]}, VertexSize -> {0.4}, VertexStyle -> {
GrayLevel[1]}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{2.692456856200017, -0.9255720392048032}, {
2.0363755348886468`, -0.16829962980165414`}}, 0.11051930238012637`], ArrowBox[{{2.692456856200017, -0.9255720392048032}, {
2.036928763730563, -1.6830935186429912`}}, 0.11051930238012637`], ArrowBox[{{2.0363755348886468`, -0.16829962980165414`}, {
0.9761551292870896, -0.46785045516391977`}}, 0.11051930238012637`],
{Arrowheads[0.], ArrowBox[{{0.9761551292870896, -0.46785045516391977`}, {
0.9759442932262589, -1.3838518355682023`}}, 0.11051930238012637`]},
{Arrowheads[0.], ArrowBox[{{0.9761551292870896, -0.46785045516391977`}, {
0.16829962980165414`, -0.9257083630823392}}, 0.11051930238012637`]},
{Arrowheads[0.], ArrowBox[{{0.9759442932262589, -1.3838518355682023`}, {
0.16829962980165414`, -0.9257083630823392}}, 0.11051930238012637`]}, ArrowBox[{{0.9759442932262589, -1.3838518355682023`}, {
2.036928763730563, -1.6830935186429912`}}, 0.11051930238012637`]},
{GrayLevel[1], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{1.5986778728024897`, -2.0196927782462994`}, 0.11051930238012637], InsetBox["1", {1.5986778728024897, -2.0196927782462994},
BaseStyle->"Graphics"]}, {
DiskBox[{0.16829962980165417`, -2.0196927782462994`}, 0.11051930238012637], InsetBox["2", {0.16829962980165417, -2.0196927782462994},
BaseStyle->"Graphics"]}, {
DiskBox[{2.692456856200017, -0.9255720392048032}, 0.11051930238012637], InsetBox["3", {2.692456856200017, -0.9255720392048032},
BaseStyle->"Graphics"]}, {
DiskBox[{2.0363755348886468`, -0.16829962980165414`}, 0.11051930238012637], InsetBox["4", {2.0363755348886468, -0.16829962980165414},
BaseStyle->"Graphics"]}, {
DiskBox[{2.036928763730563, -1.6830935186429912`}, 0.11051930238012637], InsetBox["5", {2.036928763730563, -1.6830935186429912},
BaseStyle->"Graphics"]}, {
DiskBox[{0.9761551292870896, -0.46785045516391977`}, 0.11051930238012637], InsetBox["6", {0.9761551292870896, -0.46785045516391977},
BaseStyle->"Graphics"]}, {
DiskBox[{0.9759442932262589, -1.3838518355682023`}, 0.11051930238012637], InsetBox["7", {0.9759442932262589, -1.3838518355682023},
BaseStyle->"Graphics"]}, {
DiskBox[{0.16829962980165414`, -0.9257083630823392}, 0.11051930238012637], InsetBox["8", {0.16829962980165414, -0.9257083630823392},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{149.86666666666693`, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/17605d1e722f6242.png) |
| Out[11]= |  |
Applications (3)
Count the number of Isolates:
| In[12]:= | ![g = ResourceData["Astrophysics Collaborations Network"]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/2c897b57dc87ca2d.png){kind=small} |
| Out[12]= |  |
| In[13]:= | ![Length[ResourceFunction["GraphIsolates"][g]]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/13115951b4ce5dd7.png){kind=small} |
| Out[13]= |  |
Identify if a graph is free of Isolates:
| In[14]:= | ![g = ResourceData["Marvel Universe Social Network"]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/6e66cb874228283e.png){kind=small} |
| Out[14]= |  |
| In[15]:= | ![ResourceFunction["GraphIsolates"][g] == {}](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/30d23eca8bf92f9f.png){kind=small} |
| Out[15]= |  |
Delete all isolates in a graph:
| In[16]:= | ![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {{{3, 4}, {3, 5}, {4, 6}, {7, 5}}, {{6, 7}, {6, 8}, {7, 8}}}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {
Placed[Automatic, Center]}, VertexSize -> {0.4}, VertexStyle -> {
GrayLevel[1]}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{2.692456856200017, -0.9255720392048032}, {
2.0363755348886468`, -0.16829962980165414`}}, 0.11051930238012637`], ArrowBox[{{2.692456856200017, -0.9255720392048032}, {
2.036928763730563, -1.6830935186429912`}}, 0.11051930238012637`], ArrowBox[{{2.0363755348886468`, -0.16829962980165414`}, {
0.9761551292870896, -0.46785045516391977`}}, 0.11051930238012637`],
{Arrowheads[0.], ArrowBox[{{0.9761551292870896, -0.46785045516391977`}, {
0.9759442932262589, -1.3838518355682023`}}, 0.11051930238012637`]},
{Arrowheads[0.], ArrowBox[{{0.9761551292870896, -0.46785045516391977`}, {
0.16829962980165414`, -0.9257083630823392}}, 0.11051930238012637`]},
{Arrowheads[0.], ArrowBox[{{0.9759442932262589, -1.3838518355682023`}, {
0.16829962980165414`, -0.9257083630823392}}, 0.11051930238012637`]}, ArrowBox[{{0.9759442932262589, -1.3838518355682023`}, {
2.036928763730563, -1.6830935186429912`}}, 0.11051930238012637`]},
{GrayLevel[1], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{1.5986778728024897`, -2.0196927782462994`}, 0.11051930238012637], InsetBox["1", {1.5986778728024897, -2.0196927782462994},
BaseStyle->"Graphics"]}, {
DiskBox[{0.16829962980165417`, -2.0196927782462994`}, 0.11051930238012637], InsetBox["2", {0.16829962980165417, -2.0196927782462994},
BaseStyle->"Graphics"]}, {
DiskBox[{2.692456856200017, -0.9255720392048032}, 0.11051930238012637], InsetBox["3", {2.692456856200017, -0.9255720392048032},
BaseStyle->"Graphics"]}, {
DiskBox[{2.0363755348886468`, -0.16829962980165414`}, 0.11051930238012637], InsetBox["4", {2.0363755348886468, -0.16829962980165414},
BaseStyle->"Graphics"]}, {
DiskBox[{2.036928763730563, -1.6830935186429912`}, 0.11051930238012637], InsetBox["5", {2.036928763730563, -1.6830935186429912},
BaseStyle->"Graphics"]}, {
DiskBox[{0.9761551292870896, -0.46785045516391977`}, 0.11051930238012637], InsetBox["6", {0.9761551292870896, -0.46785045516391977},
BaseStyle->"Graphics"]}, {
DiskBox[{0.9759442932262589, -1.3838518355682023`}, 0.11051930238012637], InsetBox["7", {0.9759442932262589, -1.3838518355682023},
BaseStyle->"Graphics"]}, {
DiskBox[{0.16829962980165414`, -0.9257083630823392}, 0.11051930238012637], InsetBox["8", {0.16829962980165414, -0.9257083630823392},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{149.86666666666693`, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/1292e7842f4ffa76.png) |
| In[17]:= | ![ResourceFunction["GraphIsolates"][g]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/16b1a29f7e4074dd.png){kind=small} |
| Out[17]= |  |
| In[18]:= | ![VertexDelete[g, %]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/5087f09348a4a91e.png){kind=small} |
| Out[18]= |  |
Possible Issues (1)
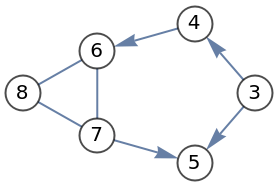If there are no isolates on the graph it returns a empty list:
| In[19]:= | ![ResourceFunction["GraphIsolates"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{3, 4, 5, 6, 7, 8}, {{{1, 2}, {1, 3}, {2, 4}, {5, 3}}, {{4, 5}, {4, 6}, {5, 6}}}, {GraphLayout -> {"Dimension" -> 2}, ImageSize -> {149.86666666666693`, Automatic}, VertexLabels -> {
Placed[Automatic, Center]}, VertexSize -> {0.4}, VertexStyle -> {
GrayLevel[1]}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{2.5250697157998934`, 0.7575043438370492}, {
1.8686026289525572`, 1.514280326539965}}, 0.18304680096463877`], ArrowBox[{{2.5250697157998934`, 0.7575043438370492}, {
1.8692822428969822`, 0.}}, 0.18304680096463877`], ArrowBox[{{1.8686026289525572`, 1.514280326539965}, {
0.8084920620143559, 1.2147185278284447`}}, 0.18304680096463877`],
{Arrowheads[0.], ArrowBox[{{0.8084920620143559, 1.2147185278284447`}, {
0.808227180246839, 0.2994845613355314}}, 0.18304680096463877`]},
{Arrowheads[0.], ArrowBox[{{0.8084920620143559, 1.2147185278284447`}, {0., 0.7572063797178915}}, 0.18304680096463877`]},
{Arrowheads[0.], ArrowBox[{{0.808227180246839, 0.2994845613355314}, {0., 0.7572063797178915}}, 0.18304680096463877`]}, ArrowBox[{{0.808227180246839, 0.2994845613355314}, {
1.8692822428969822`, 0.}}, 0.18304680096463877`]},
{GrayLevel[1], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{2.5250697157998934`, 0.7575043438370492}, 0.18304680096463877], InsetBox["3", {2.5250697157998934, 0.7575043438370492},
BaseStyle->"Graphics"]}, {
DiskBox[{1.8686026289525572`, 1.514280326539965}, 0.18304680096463877], InsetBox["4", {1.8686026289525572, 1.514280326539965},
BaseStyle->"Graphics"]}, {
DiskBox[{1.8692822428969822`, 0.}, 0.18304680096463877], InsetBox["5", {1.8692822428969822, 0.},
BaseStyle->"Graphics"]}, {
DiskBox[{0.8084920620143559, 1.2147185278284447`}, 0.18304680096463877], InsetBox["6", {0.8084920620143559, 1.2147185278284447},
BaseStyle->"Graphics"]}, {
DiskBox[{0.808227180246839, 0.2994845613355314}, 0.18304680096463877], InsetBox["7", {0.808227180246839, 0.2994845613355314},
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.7572063797178915}, 0.18304680096463877], InsetBox["8", {0., 0.7572063797178915},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{139.066666666667, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/384/3848afa6-732f-4446-8e5e-fe153d63ba33/73665e300c03093d.png) |
Related Links
Requirements
Wolfram Language 13.0 (December 2021) or above
Version History
- 1.0.0 – 22 November 2024
Related Resources
Related Symbols
License Information
This work is licensed under a Creative Commons Attribution 4.0 International License