Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the number of fundamentally different graphs of a specified size
ResourceFunction["GraphCount"][n] gives the number of nonisomorphic undirected graphs with n vertices. | |
ResourceFunction["GraphCount"][{n,m}] gives the number of nonisomorphic undirected graphs with n vertices and m edges. | |
ResourceFunction["GraphCount"][n,type] give the number of nonisomorphic graphs with n vertices and of the specified type. | |
ResourceFunction["GraphCount"][{n,m},type] give the number of nonisomorphic graphs with n vertices, m edges and of the specified type. |
Find the number of fundamentally different (nonisomorphic) graphs with four vertices:
| In[1]:= |
| Out[1]= |
Show the graphs:
| In[2]:= |
| In[3]:= |
| Out[3]= | 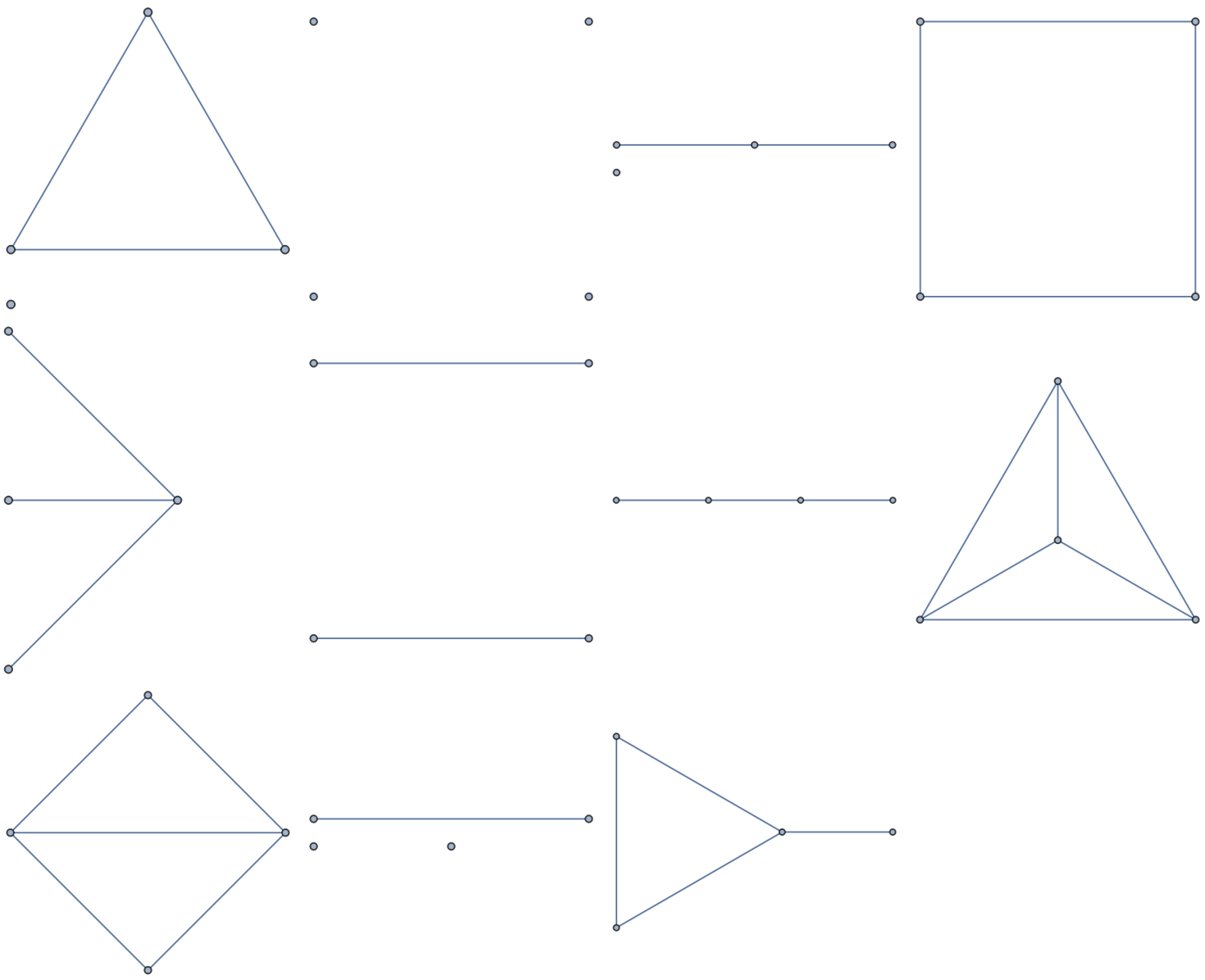 |
| In[4]:= |
| Out[4]= |
Confirm that they are nonisomorphic:
| In[5]:= |
| Out[5]= |  |
Find the number of graphs with four vertices and three edges:
| In[6]:= |
| Out[6]= |
Show the graphs:
| In[7]:= |
| Out[7]= | 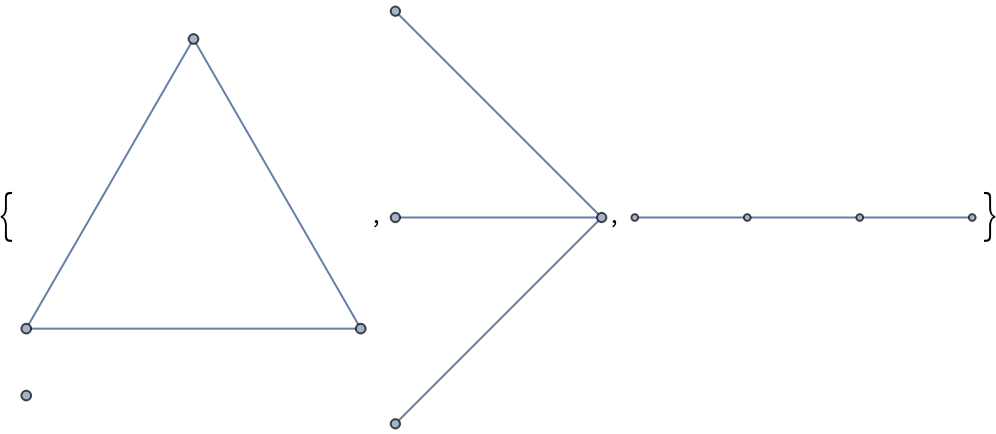 |
| In[8]:= |
| Out[8]= |
The number of nonisomorphic directed graphs with three vertices:
| In[9]:= |
| Out[9]= |
The number of simple directed unlabeled graphs on n nodes for n=1,2,… is given by OEIS A000273:
| In[10]:= |
| Out[10]= |  |
The number of simple directed unlabeled graphs on n nodes with m edges is given by OEIS A052283:
| In[11]:= |
| In[12]:= |
| Out[12]= |  |
Or as a triangle:
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |  |
Sum the rows:
| In[15]:= |
| Out[15]= |
This is the same as:
| In[16]:= |
| Out[16]= |
The number of graphs grows rapidly with the number of vertices:
| In[17]:= |
| Out[17]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License