Basic Examples (3)
Find the coordination sequence of the Petersen graph:
Show the GraphDistanceMatrix in unsorted and sorted form:
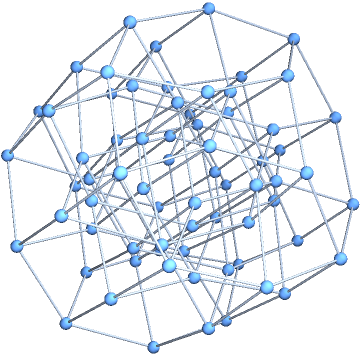
Construct the order-7 middle levels graph (here, the middle levels are 3 and 4):
Find the coordination sequence:
The coordination sequence for any odd order middle levels graph can be found with a formula:
Find the coordination sequence for a disconnected graph:
Scope (3)
Directed graphs may be used, such as seen in CayleyGraph.
The following graph is Fibonacci to ten steps in the coordination sequence:
The following graph is tribonacci to ten steps in the coordination sequence:
The following graph is Padovan to ten steps in the coordination sequence:
Properties and Relations (2)
The coordination sequences of hypercube graphs are binomial:
The coordination sequences of the Bruhat graphs are the Mahonian numbers, A008302:
Possible Issues (4)
Multiple graphs can have the same coordination sequence:
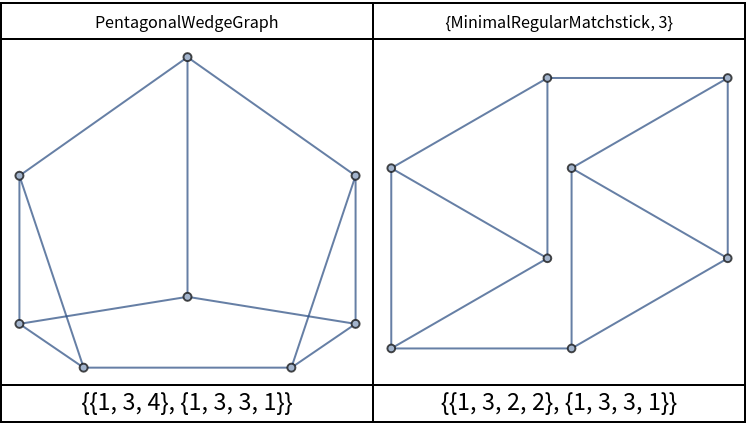
Some graphs show different distant behaviors for every vertex:
The coordination sequence for this graph has maximal dis-coordination:
Up to 9 vertices, all regular connected graphs have the same coordination sequence for all vertices, with two exceptions:
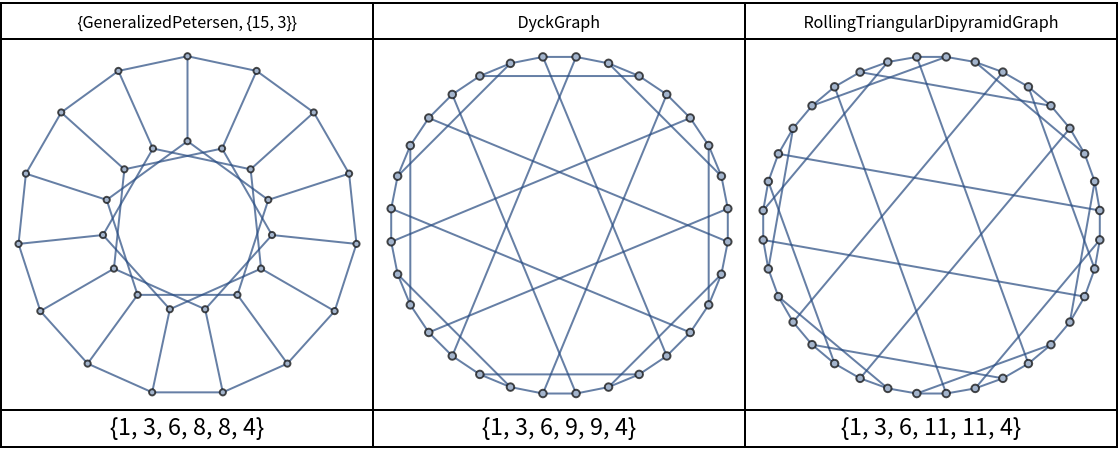
Graphs with a specific coordination sequence are hard to find. Here are several of the form {1,3,6,x,x,4}:
Determining the existence of all {1,3,6,10,10,4} graphs currently requires a search of the 453090162062723 cubic graphs on 34 nodes.
Neat Examples (2)
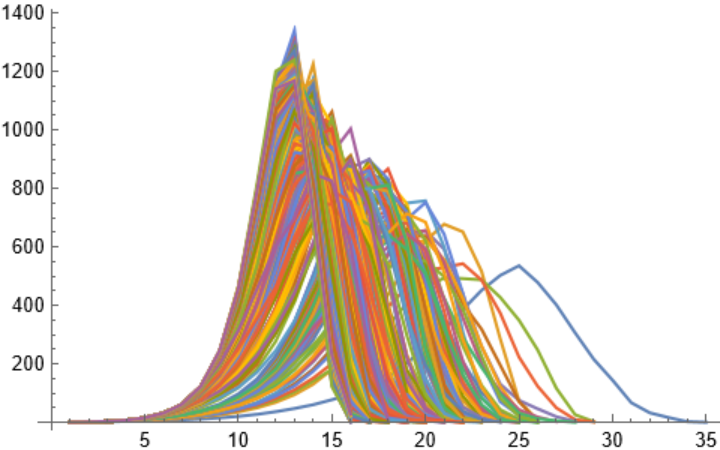
Here are 947 Cayley graphs with precomputed {order, coordination sequence, generator}:
Coordination sequences have a rise followed (usually) by a fall:
![g = Graph[PetersenGraph[], ImageSize -> 100];
gdm = GraphDistanceMatrix[g];
Row[Append[Style[MatrixForm[#], 8] & /@ {gdm, Sort[Sort /@ gdm]}, g], Spacer[20]]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/57540d5a020504c2.png)

![mlg7 = Graph3D[
UndirectedEdge @@@ Select[Subsets[Subsets[Range[7], {3, 4}], {2}], Length[Complement[#[[1]], #[[2]]]] == 0 &]]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/65101569eb507680.png)
![tribcayley = CayleyGraph[
PermutationGroup[{Cycles[{{2, 4, 3}}], Cycles[{{1, 7, 2, 6, 3}, {4, 5}}]}]]; Grid[{ResourceFunction[
"GraphCoordinationSequence"][tribcayley][[1]],
LinearRecurrence[{1, 1, 1}, {1, 2, 4}, 18]}, Frame -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/0fd5acc0a19d0efe.png)
![padovancayley = CayleyGraph[
PermutationGroup[{Cycles[{{1, 5}, {2, 4}, {3, 6}}], Cycles[{{1, 3, 4}, {2, 5, 7}}]}]];
ResourceFunction["GraphCoordinationSequence"][padovancayley][[1]]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/4860884d3c3def13.png)
![Column[Table[
ResourceFunction["GraphCoordinationSequence"][
GraphData[{"Hypercube", n}]], {n, 2, 10}], Alignment -> Center]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/1f12dc5251eec1c3.png)

![Column[
Table[ResourceFunction["GraphCoordinationSequence"][
GraphData[{"Bruhat", n}]][[1]], {n, 3, 6}], Alignment -> Center]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/2ffa8af79f9fe289.png)

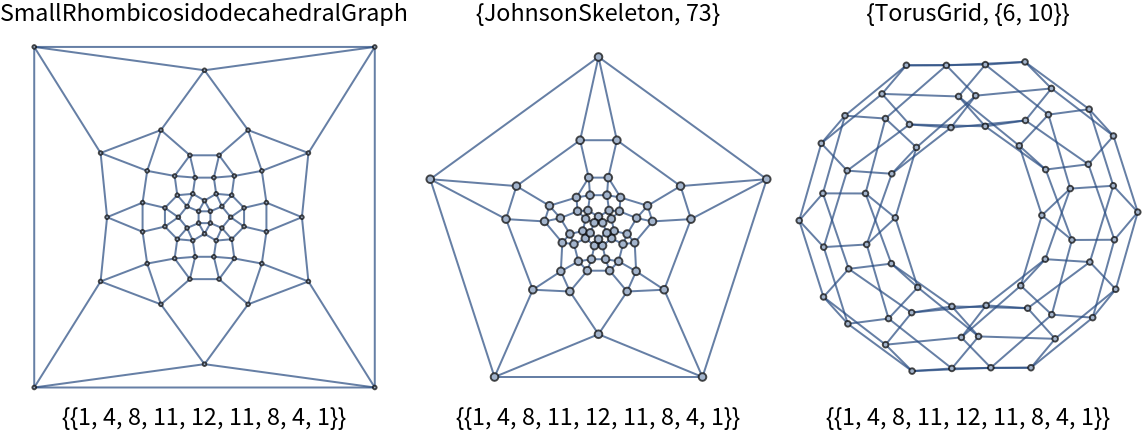
![graphs = {"SmallRhombicosidodecahedralGraph", {"JohnsonSkeleton", 73}, {"TorusGrid", {6, 10}}};
Grid[{graphs, GraphData /@ graphs, ResourceFunction["GraphCoordinationSequence"][GraphData[#]] & /@ graphs}]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/4501f5e469923bed.png)
![g = Graph[GraphData[{"UniquelyPancyclic", {14, 3}}], ImageSize -> 100];
gdm = GraphDistanceMatrix[g];
Row[Append[Style[MatrixForm[#], 8] & /@ {gdm, Sort[Sort /@ gdm]}, g], Spacer[20]]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/75029a72b2b8cf5b.png)

![graphs = {"PentagonalWedgeGraph", {"MinimalRegularMatchstick", 3}};
Grid[{Style[#, 9] & /@ graphs, GraphData[#] & /@ graphs, ResourceFunction["GraphCoordinationSequence"][GraphData[#]] & /@ graphs}, Frame -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/003d3b559c013abf.png)
![graphs = {{"GeneralizedPetersen", {15, 3}}, "DyckGraph", "RollingTriangularDipyramidGraph"};
Grid[{Style[#, 9] & /@ graphs, GraphData[#] & /@ graphs, ResourceFunction["GraphCoordinationSequence"][GraphData[#]][[1]] & /@
graphs}, Frame -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/33b/33b77472-a205-435b-9057-699c59e41d99/3b148f9f3c7a2ee8.png)