Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GramianReduce

Source Notebook

Find a unimodular conversion matrix corresponding to a lattice Gramian matrix

Contributed by: Daniel Lichtblau

ResourceFunction["GramianReduce"][mat]

treats mat as the Gram matrix of an integer lattice and returns matrices {u,b} where u is unimodular (invertible over the integers) and b satisfies b==u.mat.Transpose[u].

Details and Options

A Gram matrix for a lattice given by generating vectors V={v1,v2,…} is the matrix of inner products V.Vt.
The matrix mat should contain only integers or rationals.
Gram matrices are symmetric and positive definite.
ResourceFunction["GramianReduce"] treats its input as symmetric and positive definite without regard to how it might be decomposed into a product of a lattice and its transpose.
Given an actual lattice, one can similarly obtain a unimodular transformation matrix for its Gramian using the resource function ExtendedLatticeReduce.

Examples

Basic Examples (3) 

Reduce a 3×3 Gramian matrix:

In[1]:=
gmat = {{12, 692, 609}, {692, 39930, 35139}, {609, 35139, 30923}}; {uu, bb} = ResourceFunction["GramianReduce"][gmat]
Out[1]=

Check unimodularity:

In[2]:=
Det[uu]
Out[2]=

Check the matrix identity:

In[3]:=
bb == uu . gmat . Transpose[uu]
Out[3]=

Properties and Relations (6) 

Reduce a larger Gramian:

In[4]:=
bigGramian = {{5134555716833684462050, 1134820115468538586617, 4115713492900717547967, 3259415496164683676787, 6901434316369918214148, 2650511708397427356831}, {1134820115468538586617, 250813656622696545362, 909639454478297119911, 720383704784980390971, 1525328951465954294884, 585806088950015116423}, {4115713492900717547967, 909639454478297119911, 3299038610119673996962, 2612654546245174311021, 5531993010247778025084, 2124574627864725467073}, {3259415496164683676787, 720383704784980390971, 2612654546245174311021, 2069076656780310612682, 4381029868424634491724, 1682544588384361936653}, {6901434316369918214148, 1525328951465954294884, 5531993010247778025084, 4381029868424634491724, 9276322675205107130897, 3562593039998124079612}, {2650511708397427356831, 585806088950015116423, 2124574627864725467073, 1682544588384361936653, 3562593039998124079612, 1368222043694964849890}};
In[5]:=
{ubig, bbig} = ResourceFunction["GramianReduce"][bigGramian]
Out[5]=

Check that the transformation matrix unimodularity and the matrix product identity properties both hold:

In[6]:=
{Abs[Det[ubig]] == 1, ubig . bigGramian . Transpose[ubig] == bbig}
Out[6]=

This matrix is the Gramian of a certain matrix:

In[7]:=
mat = {{1, 0, 0, 0, 0, 0, 71655814257}, {0, 1, 0, 0, 0, 0, 15837097481}, {0, 0, 1, 0, 0, 0, 57437258031}, {0, 0, 0, 1, 0, 0, 45487104291}, {0, 0, 0, 0, 1, 0, 96313668164}, {0, 0, 0, 0, 0, 1, 36989485583}}; mat . Transpose[mat] === bigGramian
Out[7]=

Compute the lattice reduction and unimodular transformation of this lattice using the resource function ExtendedLatticeReduce:

In[8]:=
{umat, redlat} = ResourceFunction["ExtendedLatticeReduce"][mat]
Out[8]=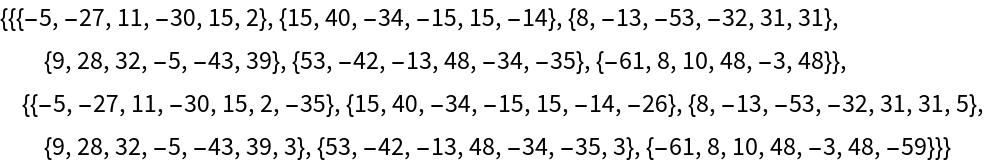

The transformation is the same as the one obtained by GramianReduce:

In[9]:=
umat == ubig
Out[9]=

In this example, the reduced lattice also gives rise to the reduced Gramian:

In[10]:=
redlat . Transpose[redlat]
Out[10]=

Version History

  • 1.0.0 – 17 January 2020

Related Resources

Author Notes

A different Wolfram Language implementation by Wilberd van der Kallen can be found at the links below:

License Information