Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GramP

Source Notebook

Evaluate the Gram polynomial

Contributed by: Jan Mangaldan

ResourceFunction["GramP"][k,m,t]

gives the Gram polynomial .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
Explicit formulas are given for nonnegative integer k.
For certain special arguments, ResourceFunction["GramP"] automatically evaluates to exact values.
ResourceFunction["GramP"] can be evaluated to arbitrary numerical precision.
ResourceFunction["GramP"] automatically threads over lists.

Examples

Basic Examples (2) 

Compute the fifth Gram polynomial:

In[1]:=
ResourceFunction["GramP"][5, m, t]
Out[1]=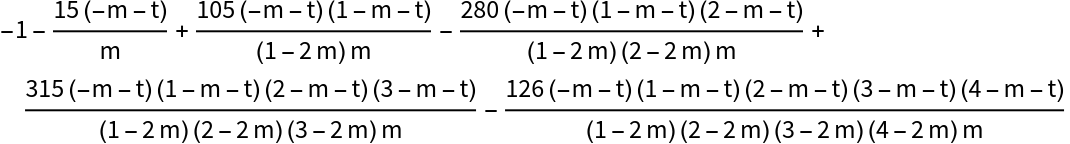

Plot over a subset of the reals:

In[2]:=
Plot[ResourceFunction["GramP"][5, 3, t], {t, -3, 3}]
Out[45]=

Scope (2) 

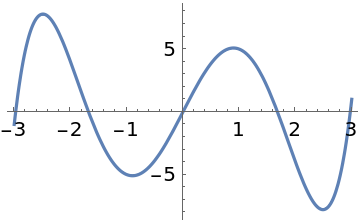Evaluate to high precision:

In[46]:=
N[ResourceFunction["GramP"][7, 6, 8/3], 50]
Out[46]=

GramP threads elementwise over lists:

In[47]:=
ResourceFunction["GramP"][{3, 5, 7}, 7, t]
Out[47]=

Applications (2) 

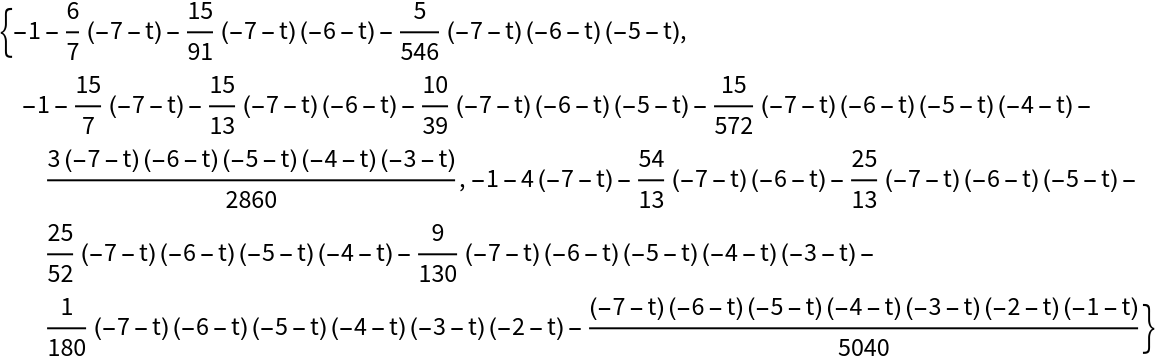Plot the first few Gram polynomials:

In[48]:=
With[{m = 9}, Plot[Evaluate[ Table[ResourceFunction["GramP"][n, m, x], {n, 0, 5}]], {x, -m, m}, PlotRange -> All]]
Out[86]=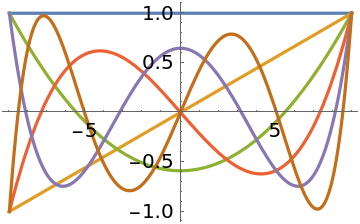

Use Gram polynomials to construct a quartic least-squares fit for equispaced data:

In[87]:=
data = {{1., 5.}, {2., 4.}, {3., 3.}, {4., 2.}, {5., 1.}, {6., 0.}, {7., 1.}, {8., 2.}, {9., 3.}, {10., 4.}, {11., 5.}}; deg = 4; m = Quotient[Length[data], 2];

Construct the basis functions and the design matrix:

In[88]:=
gbasis = Table[ResourceFunction["GramP"][k, m, Rescale[x, MinMax[data[[All, 1]]], {-m, m}]], {k, 0, deg}]; dm = DesignMatrix[data, gbasis, x];

The normal equations are easily solved in the Gram basis:

In[89]:=
coef = Transpose[dm] . data[[All, 2]]/Total[dm^2]
Out[89]=

Show the data with the curve:

In[90]:=
Show[ListPlot[data, PlotStyle -> Black], Plot[coef . gbasis // Evaluate, {x, 1, Length[data]}]]
Out[90]=

Properties and Relations (3) 

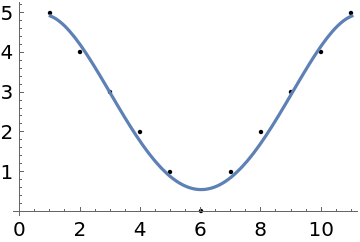GramP can be represented as a DifferenceRoot:

In[91]:=
gp[k_Integer?NonNegative, m_, t_] := DifferenceRoot[ Function[{\[FormalY], \[FormalN]}, {-(1 + \[FormalN]) (2 + \[FormalN] + 2 m) \[FormalY][\[FormalN]] + 2 t (3 + 2 \[FormalN]) \[FormalY][ 1 + \[FormalN]] + (2 + \[FormalN]) (1 + \[FormalN] - 2 m) \[FormalY][2 + \[FormalN]] == 0, \[FormalY][-1] == 0, \[FormalY][0] == 1}]][k]
In[92]:=
gp[5, m, t] == ResourceFunction["GramP"][5, m, t] // Simplify
Out[92]=

GramP satisfies a discrete orthogonality relation:

In[93]:=
With[{n1 = 5, n2 = 3, m = 4}, \!\( \*UnderoverscriptBox[\(\[Sum]\), \(t = \(-m\)\), \(m\)]\(\* InterpretationBox[ TagBox[ DynamicModuleBox[{Typeset`open = False}, FrameBox[ PaneSelectorBox[{False->GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"], ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"], ImageSizeCache->{11., {1., 10.}}]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{ {GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]}, { StyleBox[ PaneBox[GridBox[{ { RowBox[{ TagBox["\<\"Version (latest): \"\>", "IconizedLabel"], " ", TagBox["\<\"1.0.0\"\>", "IconizedItem"]}]}, { TagBox[ TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/a5f86a99-f129-4a6e-8471-eb187a107f36/"}, "HyperlinkURL"], "IconizedItem"]} }, DefaultBaseStyle->"Column", GridBoxAlignment->{"Columns" -> {{Left}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle", FontFamily->"Roboto", FontSize->11]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, { GrayLevel[0.8]}, False}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open], BaselinePosition->Baseline, ImageSize->Automatic], Background->RGBColor[ 0.9686274509803922, 0.9764705882352941, 0.984313725490196], BaselinePosition->Baseline, DefaultBaseStyle->{}, FrameMargins->{{0, 0}, {1, 0}}, FrameStyle->RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627], RoundingRadius->4]], {"FunctionResourceBox", RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784], "GramP"}, TagBoxNote->"FunctionResourceBox"], ResourceFunction["GramP"], BoxID -> "GramP", Selectable->False][n1, m, t] \* InterpretationBox[ TagBox[ DynamicModuleBox[{Typeset`open = False}, FrameBox[ PaneSelectorBox[{False->GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"], ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"], ImageSizeCache->{11., {1., 10.}}]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{ {GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]}, { StyleBox[ PaneBox[GridBox[{ { RowBox[{ TagBox["\<\"Version (latest): \"\>", "IconizedLabel"], " ", TagBox["\<\"1.0.0\"\>", "IconizedItem"]}]}, { TagBox[ TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/a5f86a99-f129-4a6e-8471-eb187a107f36/"}, "HyperlinkURL"], "IconizedItem"]} }, DefaultBaseStyle->"Column", GridBoxAlignment->{"Columns" -> {{Left}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle", FontFamily->"Roboto", FontSize->11]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, { GrayLevel[0.8]}, False}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open], BaselinePosition->Baseline, ImageSize->Automatic], Background->RGBColor[ 0.9686274509803922, 0.9764705882352941, 0.984313725490196], BaselinePosition->Baseline, DefaultBaseStyle->{}, FrameMargins->{{0, 0}, {1, 0}}, FrameStyle->RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627], RoundingRadius->4]], {"FunctionResourceBox", RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784], "GramP"}, TagBoxNote->"FunctionResourceBox"], ResourceFunction["GramP"], BoxID -> "GramP", Selectable->False][n2, m, t]\)\)]
Out[93]=

The elements of SavitzkyGolayMatrix can be expressed in terms of GramP:

In[94]:=
With[{r = 5, k = 2}, Table[\!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 0\), \(k\)]\( \*FractionBox[\(Binomial[2 r, j]\), \(Binomial[2 r + j + 1, j + 1]\)] \((1 + \*FractionBox[\(j\), \(j + 1\)])\) \* InterpretationBox[ TagBox[ DynamicModuleBox[{Typeset`open = False}, FrameBox[ PaneSelectorBox[{False->GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"], ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"], ImageSizeCache->{11., {1., 10.}}]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{ {GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]}, { StyleBox[ PaneBox[GridBox[{ { RowBox[{ TagBox["\<\"Version (latest): \"\>", "IconizedLabel"], " ", TagBox["\<\"1.0.0\"\>", "IconizedItem"]}]}, { TagBox[ TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/a5f86a99-f129-4a6e-8471-eb187a107f36/"}, "HyperlinkURL"], "IconizedItem"]} }, DefaultBaseStyle->"Column", GridBoxAlignment->{"Columns" -> {{Left}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle", FontFamily->"Roboto", FontSize->11]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, { GrayLevel[0.8]}, False}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open], BaselinePosition->Baseline, ImageSize->Automatic], Background->RGBColor[ 0.9686274509803922, 0.9764705882352941, 0.984313725490196], BaselinePosition->Baseline, DefaultBaseStyle->{}, FrameMargins->{{0, 0}, {1, 0}}, FrameStyle->RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627], RoundingRadius->4]], {"FunctionResourceBox", RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784], "GramP"}, TagBoxNote->"FunctionResourceBox"], ResourceFunction["GramP"], BoxID -> "GramP", Selectable->False][j, r, i] \* InterpretationBox[ TagBox[ DynamicModuleBox[{Typeset`open = False}, FrameBox[ PaneSelectorBox[{False->GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"], ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"], ImageSizeCache->{11., {1., 10.}}]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{ {GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]}, { StyleBox[ PaneBox[GridBox[{ { RowBox[{ TagBox["\<\"Version (latest): \"\>", "IconizedLabel"], " ", TagBox["\<\"1.0.0\"\>", "IconizedItem"]}]}, { TagBox[ TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/a5f86a99-f129-4a6e-8471-eb187a107f36/"}, "HyperlinkURL"], "IconizedItem"]} }, DefaultBaseStyle->"Column", GridBoxAlignment->{"Columns" -> {{Left}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle", FontFamily->"Roboto", FontSize->11]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, { GrayLevel[0.8]}, False}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open], BaselinePosition->Baseline, ImageSize->Automatic], Background->RGBColor[ 0.9686274509803922, 0.9764705882352941, 0.984313725490196], BaselinePosition->Baseline, DefaultBaseStyle->{}, FrameMargins->{{0, 0}, {1, 0}}, FrameStyle->RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627], RoundingRadius->4]], {"FunctionResourceBox", RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784], "GramP"}, TagBoxNote->"FunctionResourceBox"], ResourceFunction["GramP"], BoxID -> "GramP", Selectable->False][j, r, 0]\)\), {i, -r, r}] == SavitzkyGolayMatrix[{r}, k, WorkingPrecision -> \[Infinity]]]
Out[94]=
In[95]:=
With[{r = 5, k = 2}, KroneckerProduct[#, #] &[Table[\!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 0\), \(k\)]\( \*FractionBox[\(Binomial[2 r, j]\), \(Binomial[2 r + j + 1, j + 1]\)] \((1 + \*FractionBox[\(j\), \(j + 1\)])\) \* InterpretationBox[ TagBox[ DynamicModuleBox[{Typeset`open = False}, FrameBox[ PaneSelectorBox[{False->GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"], ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"], ImageSizeCache->{11., {1., 10.}}]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{ {GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]}, { StyleBox[ PaneBox[GridBox[{ { RowBox[{ TagBox["\<\"Version (latest): \"\>", "IconizedLabel"], " ", TagBox["\<\"1.0.0\"\>", "IconizedItem"]}]}, { TagBox[ TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/a5f86a99-f129-4a6e-8471-eb187a107f36/"}, "HyperlinkURL"], "IconizedItem"]} }, DefaultBaseStyle->"Column", GridBoxAlignment->{"Columns" -> {{Left}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle", FontFamily->"Roboto", FontSize->11]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, { GrayLevel[0.8]}, False}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open], BaselinePosition->Baseline, ImageSize->Automatic], Background->RGBColor[ 0.9686274509803922, 0.9764705882352941, 0.984313725490196], BaselinePosition->Baseline, DefaultBaseStyle->{}, FrameMargins->{{0, 0}, {1, 0}}, FrameStyle->RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627], RoundingRadius->4]], {"FunctionResourceBox", RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784], "GramP"}, TagBoxNote->"FunctionResourceBox"], ResourceFunction["GramP"], BoxID -> "GramP", Selectable->False][j, r, i] \* InterpretationBox[ TagBox[ DynamicModuleBox[{Typeset`open = False}, FrameBox[ PaneSelectorBox[{False->GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"], ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"], ImageSizeCache->{11., {1., 10.}}]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{ {GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["GramP", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]}, { StyleBox[ PaneBox[GridBox[{ { RowBox[{ TagBox["\<\"Version (latest): \"\>", "IconizedLabel"], " ", TagBox["\<\"1.0.0\"\>", "IconizedItem"]}]}, { TagBox[ TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/a5f86a99-f129-4a6e-8471-eb187a107f36/"}, "HyperlinkURL"], "IconizedItem"]} }, DefaultBaseStyle->"Column", GridBoxAlignment->{"Columns" -> {{Left}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle", FontFamily->"Roboto", FontSize->11]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, { GrayLevel[0.8]}, False}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open], BaselinePosition->Baseline, ImageSize->Automatic], Background->RGBColor[ 0.9686274509803922, 0.9764705882352941, 0.984313725490196], BaselinePosition->Baseline, DefaultBaseStyle->{}, FrameMargins->{{0, 0}, {1, 0}}, FrameStyle->RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627], RoundingRadius->4]], {"FunctionResourceBox", RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784], "GramP"}, TagBoxNote->"FunctionResourceBox"], ResourceFunction["GramP"], BoxID -> "GramP", Selectable->False][j, r, 0]\)\), {i, -r, r}]] == SavitzkyGolayMatrix[r, k, WorkingPrecision -> \[Infinity]]]
Out[95]=

Version History

  • 1.0.0 – 06 January 2021

Source Metadata

  • Citation:
    • Hamming, R.W., Numerical Methods for Scientists and Engineers, Second Edition. New York: McGraw-Hill, 1973.
    • Ralston, A., Rabinowitz P., A First Course in Numerical Analysis, Second Edition. New York: McGraw-Hill, 1978.

Related Resources

License Information