Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Show the graceful graph corresponding to a given permutation
ResourceFunction["GracefulGraphFromPermutation"][perm] shows the graceful graph for the permutation perm. |
Every permutation can be converted to a graceful graph:
| In[1]:= |
| Out[1]= | 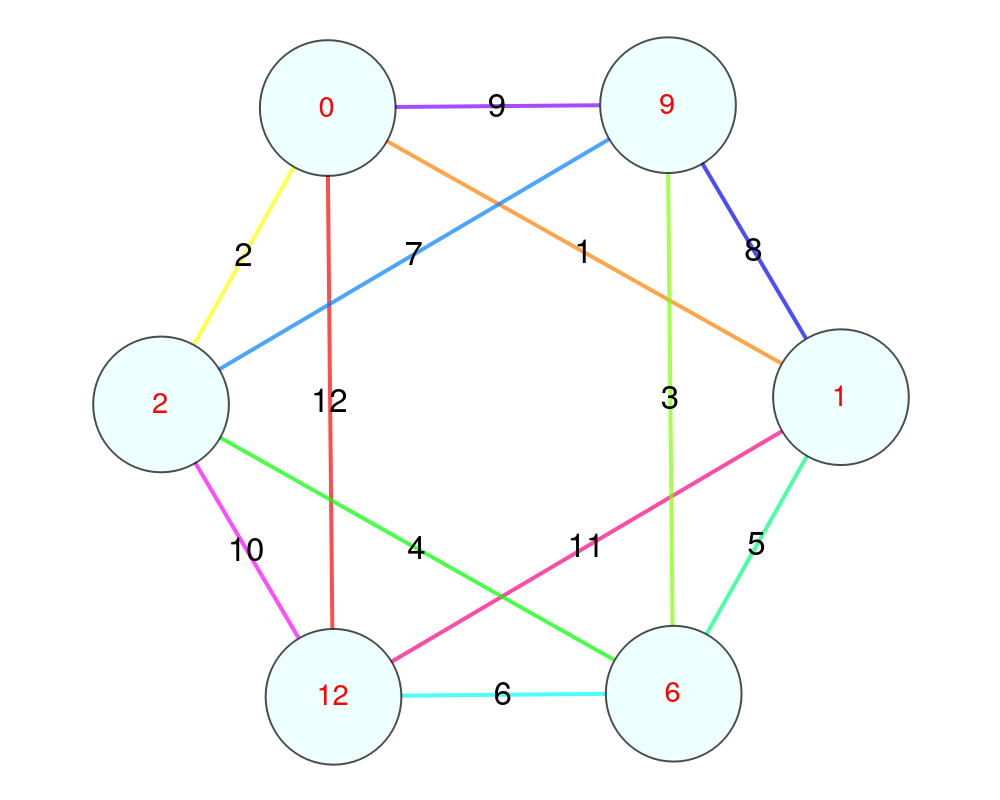 |
Some graceful graphs are planar:
| In[2]:= |
| Out[2]= | 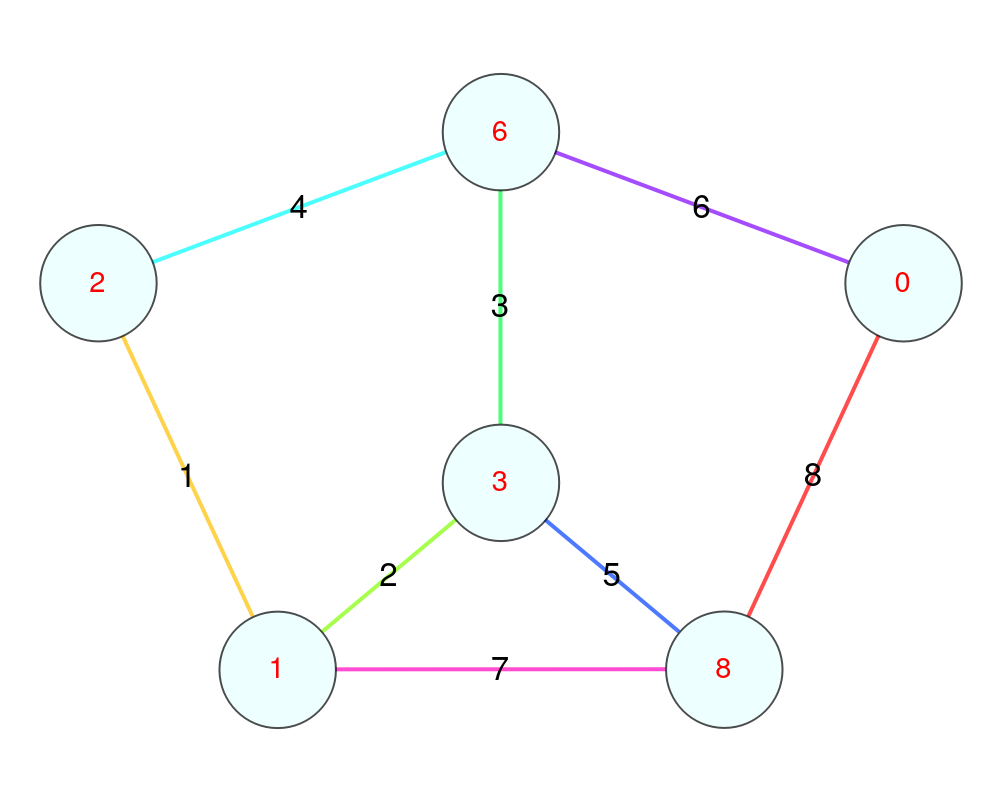 |
Any random permutation can give a graceful graph:
| In[3]:= |
| Out[3]= | 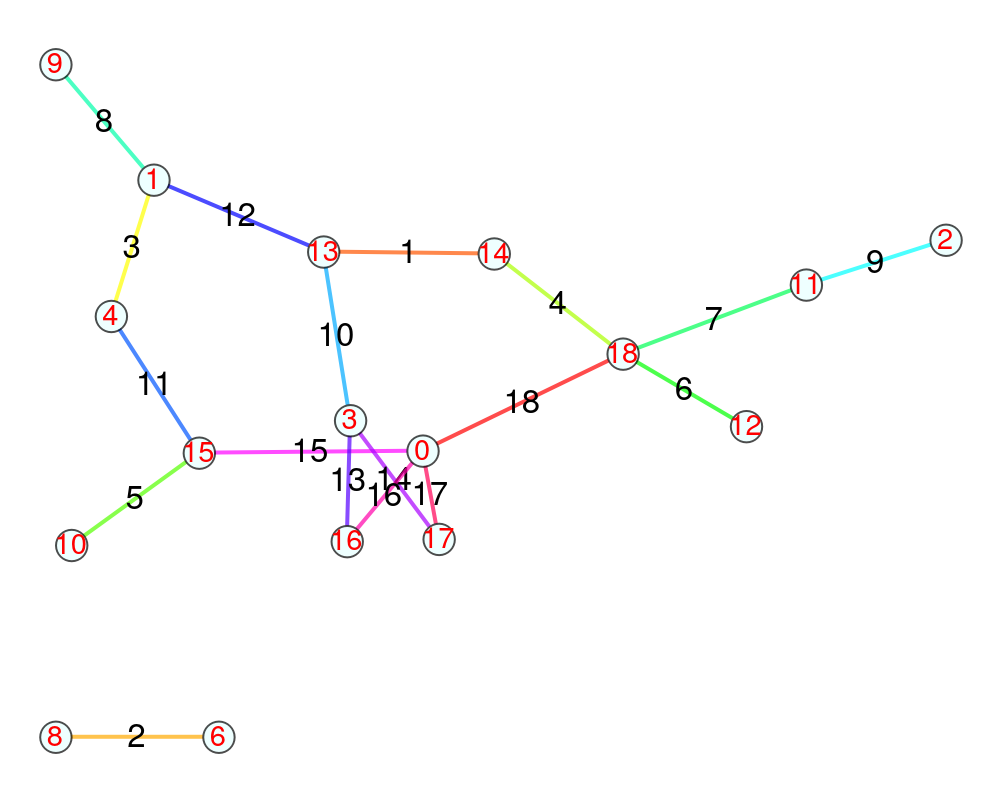 |
Some graceful graphs are trees:
| In[4]:= |
| Out[4]= | 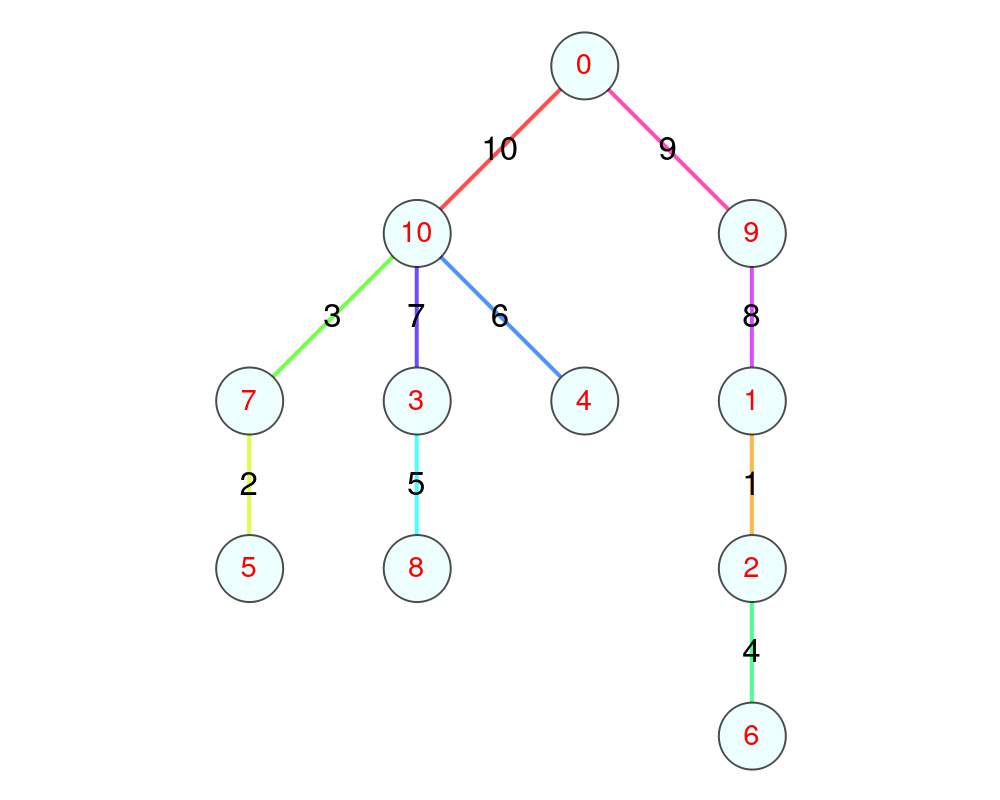 |
This work is licensed under a Creative Commons Attribution 4.0 International License