Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the global extrema of an expression with respect to the given variables
ResourceFunction["GlobalExtrema"][expr,x] computes the global maxima and minima of expr with respect to x. | |
ResourceFunction["GlobalExtrema"][expr,{x,y,…}] computes the global maxima and minima of expr with respect to multiple variables. | |
ResourceFunction["GlobalExtrema"][{expr,const},{x,y,…}] computes the global maxima and minima of expr subject to the constraint const. |
Compute the global extrema of a curve:
| In[1]:= |
|
| Out[1]= |

|
Plot the result:
| In[2]:= |
|
| Out[2]= |
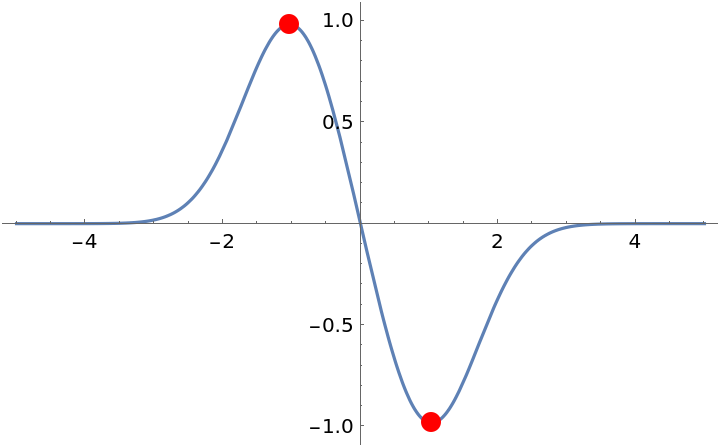
|
Use a constraint in order to reduce the domain upon which extrema can be found:
| In[3]:= |
|
| Out[3]= |
|
Compute the extrema of a function of two variables:
| In[4]:= |
|
| Out[4]= |
|
Compute the extrema of a piecewise function:
| In[5]:= |
|
| Out[5]= |
|
Plot the result:
| In[6]:= |
|
| Out[6]= |
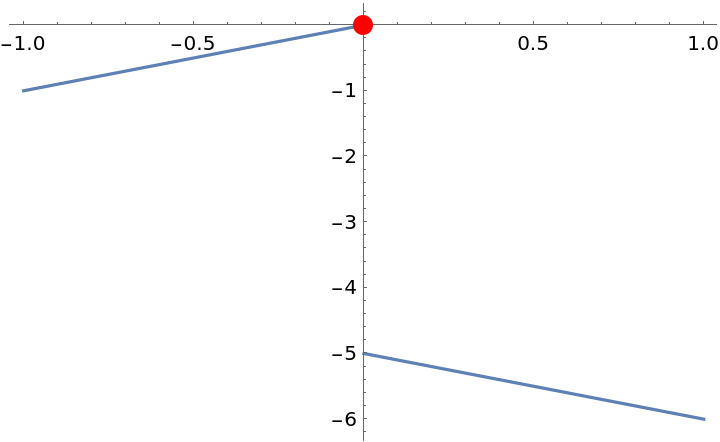
|
GlobalExtrema may return duplicate results for periodic functions:
| In[7]:= |
|
| Out[7]= |
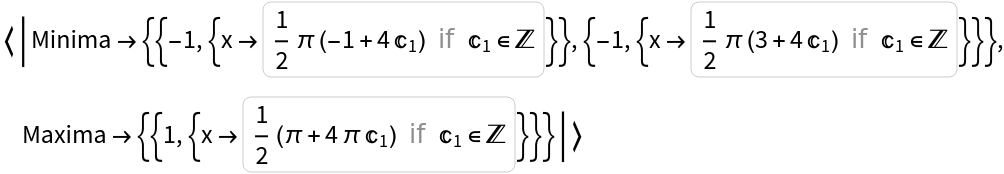
|
This work is licensed under a Creative Commons Attribution 4.0 International License