Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GeothmeticMeandian

Source Notebook

Calculate the geothmetic meandian of a list of numbers

Contributed by: Sander Huisman

ResourceFunction["GeothmeticMeandian"][x1,x2,…]

gives the geothmetic meandian of the xi.

ResourceFunction["GeothmeticMeandian"][list]

gives the geothmetic meandian of the elements in list.

Details

As defined by the xkcd comic website, the geothmetic meandian is the number obtained by iteratively calculating {Mean[list],GeometricMean[list],Median[list]} to convergence.
For negative numbers, the geometric mean generally gives complex numbers. For complex numbers, the Median is modified so as to order by the absolute value of the numbers.

Examples

Basic Examples (1) 

Compute the geothmetic meandian of some numbers:

In[1]:=
ResourceFunction["GeothmeticMeandian"][1, 1, 2, 3, 5]
Out[1]=

Scope (3) 

The input can be given as multiple arguments:

In[2]:=
ResourceFunction["GeothmeticMeandian"][1, 1, 2, 3, 5]
Out[2]=

The input can also be given as a list:

In[3]:=
ResourceFunction["GeothmeticMeandian"][{1, 1, 2, 3, 5}]
Out[3]=

The input can also contain complex numbers:

In[4]:=
ResourceFunction["GeothmeticMeandian"][ RandomComplex[{-1 - I, 1 + I}, 100]]
Out[4]=

Possible Issues (2) 

Due to the GeometricMean operation, negative numbers can result in complex answers:

In[5]:=
ResourceFunction["GeothmeticMeandian"][{1, 2, 3, -14, 5}]
Out[5]=

Sometimes a real result is returned:

In[6]:=
ResourceFunction["GeothmeticMeandian"][{8, 2, -3, -4, 15}]
Out[6]=

Symbolic values are not allowed and will be left unevaluated:

In[7]:=
ResourceFunction["GeothmeticMeandian"][{1, 2, 3, a, 5}]
Out[7]=

Neat Examples (1) 

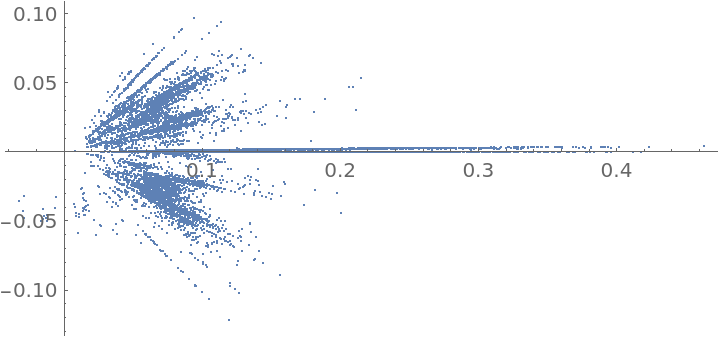
Find the distribution of the geothmetic meandian of 100 random variates of a normal distribution:

In[8]:=
dist = NormalDistribution[]; alldata = ResourceFunction["GeothmeticMeandian"] /@ RandomVariate[dist, {10000, 100}]; ComplexListPlot[alldata, PlotRange -> All]
Out[8]=

Publisher

SHuisman

Version History

  • 1.0.0 – 17 March 2021

License Information