Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Create an interface for constructing a GeometricScene
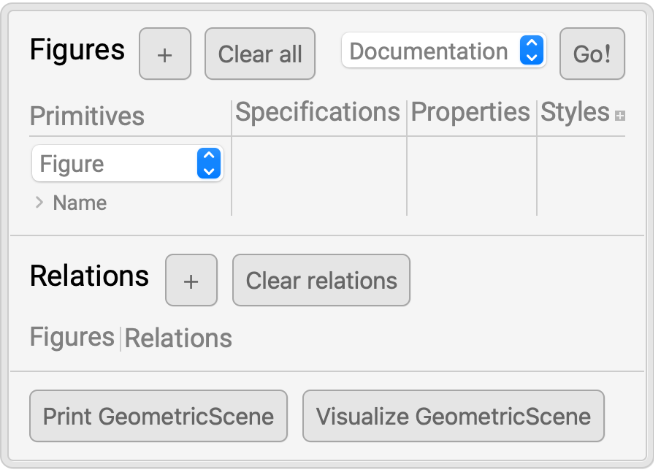
ResourceFunction["GeometricSceneConstructor"][] creates an interactive tool for generating a GeometricScene. |
| Figures | area for adding primitives such as Line,Circle,Triangle, etc. |
| Relations | area for adding relationships among the defined primitives such as "Parallel", "Inside", etc. |
Create an interface for constructing GeometricScene expressions:
| In[1]:= |
Add some figures, specifying the points and constants as needed:
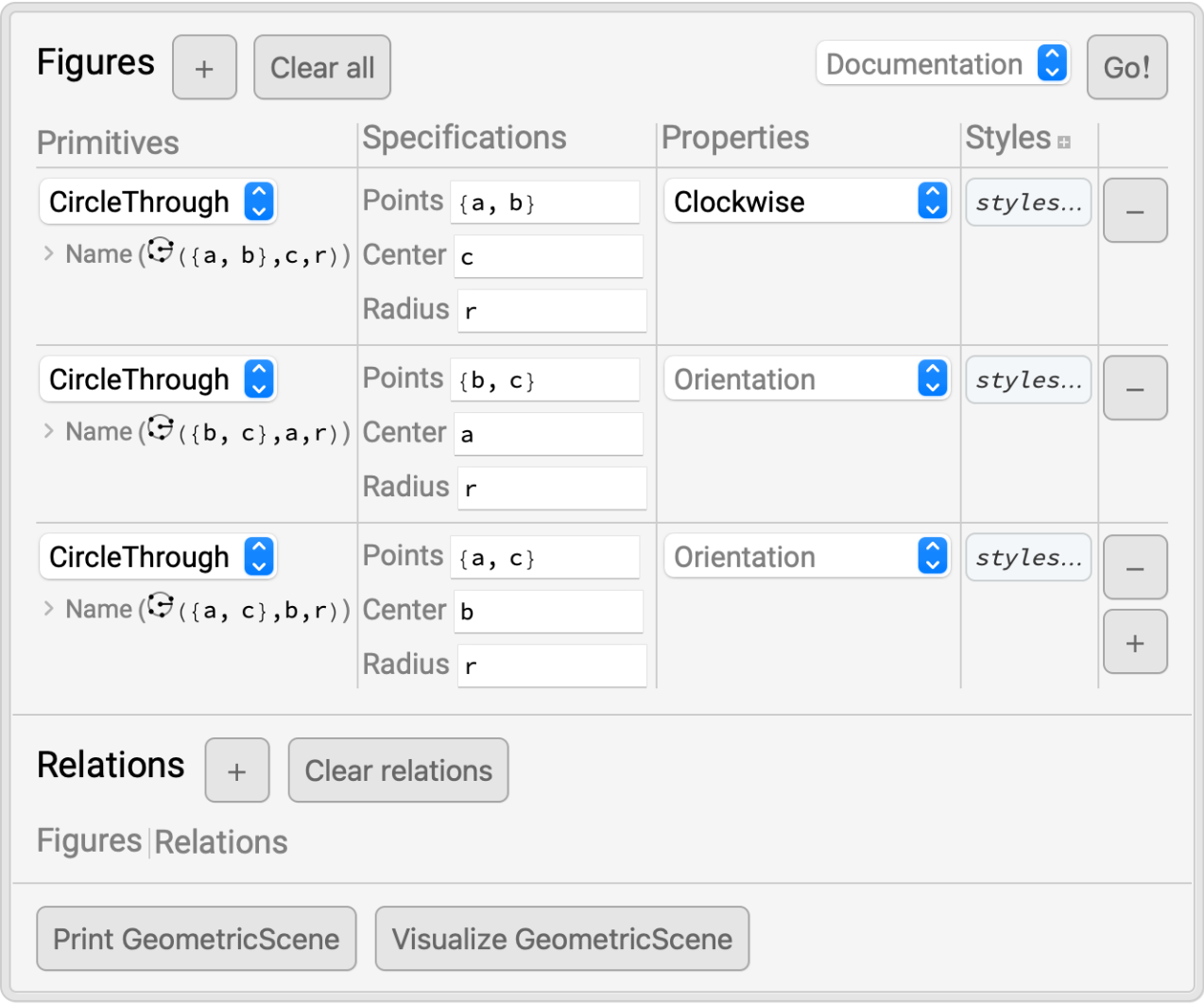
Click Visualize GeometricScene to create and evaluate code that generates an instance of the scene. Even without any relations, we are able to build interesting scenes:
| In[2]:= | ![RandomInstance[
GeometricScene[{{a, b, c}, {r}}, {GeometricAssertion[
CircleThrough[{a, b}, c, r], "Clockwise"], CircleThrough[{b, c}, a, r], CircleThrough[{a, c}, b, r]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/0f2/0f291348-ccb5-49ec-a7a6-03d93a45ccb8/7a6c2466ff746ab4.png) |
| Out[2]= | 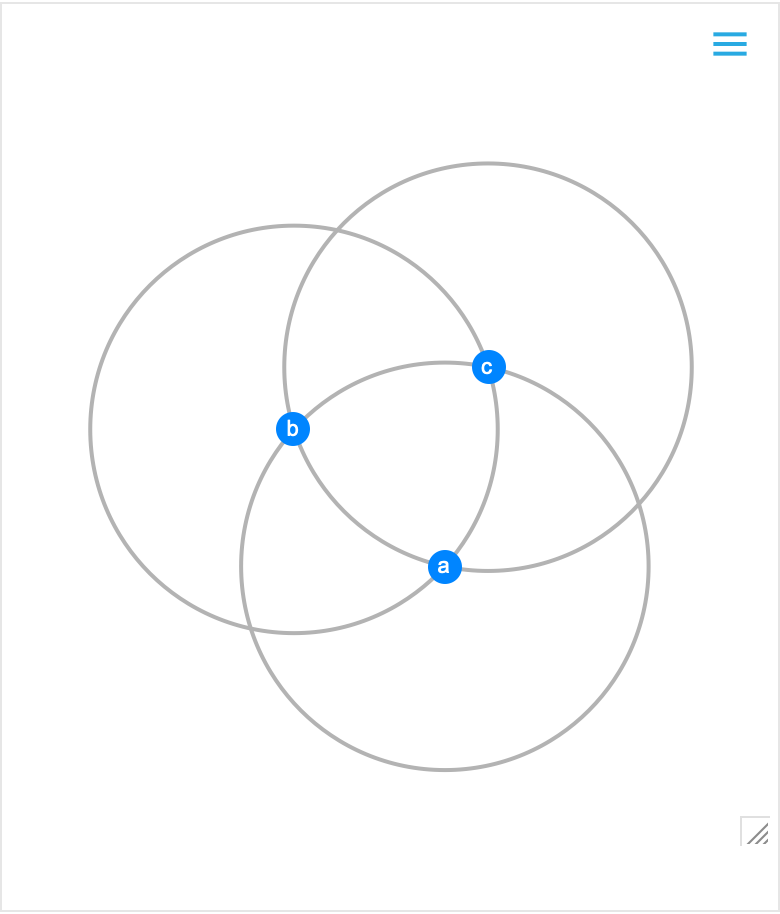 |
Construct famous scenes like Thales's theorem:
| In[3]:= |
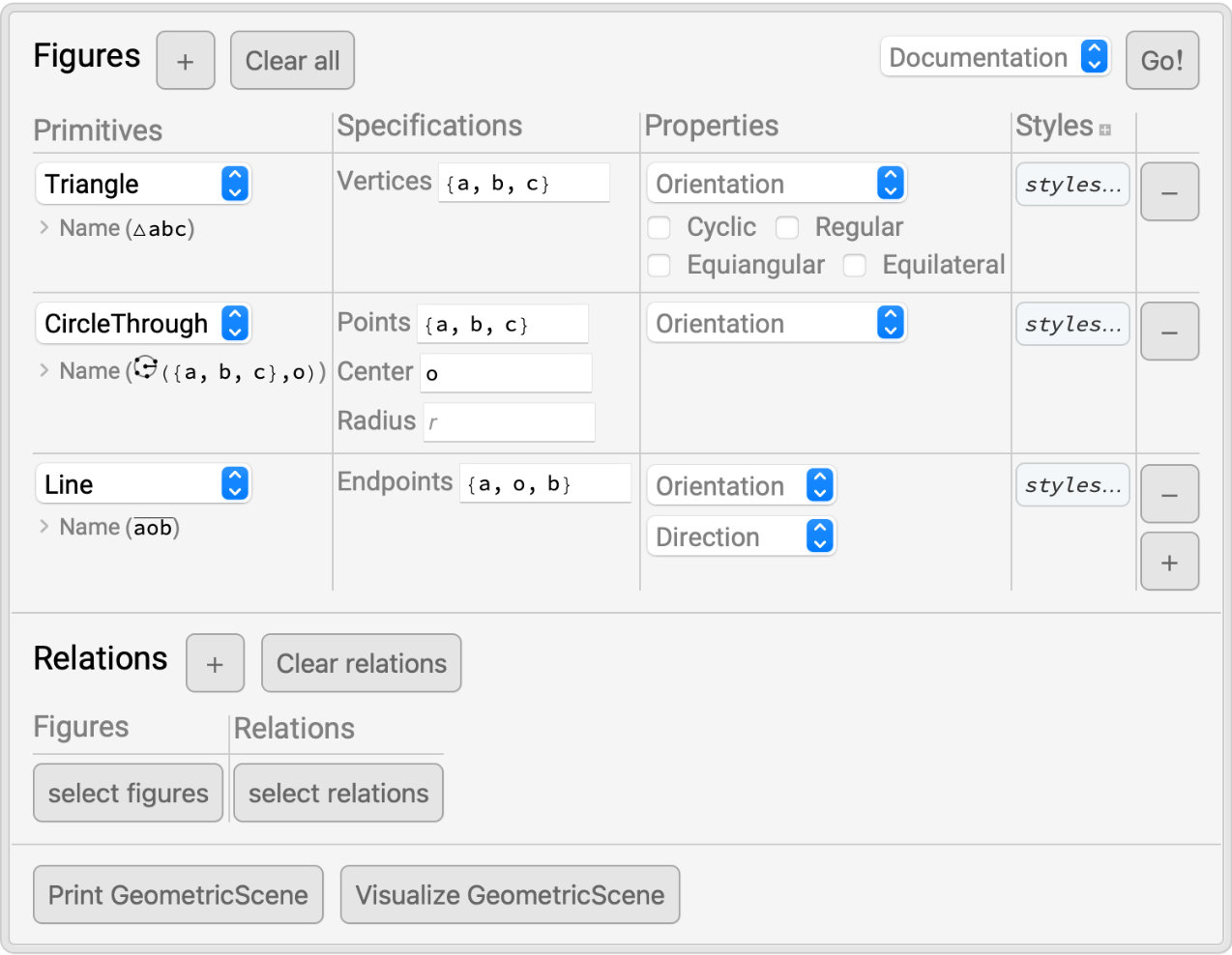
| In[4]:= |
| Out[4]= |  |
Use the "Properties" column to state properties of individual figures:
| In[5]:= |
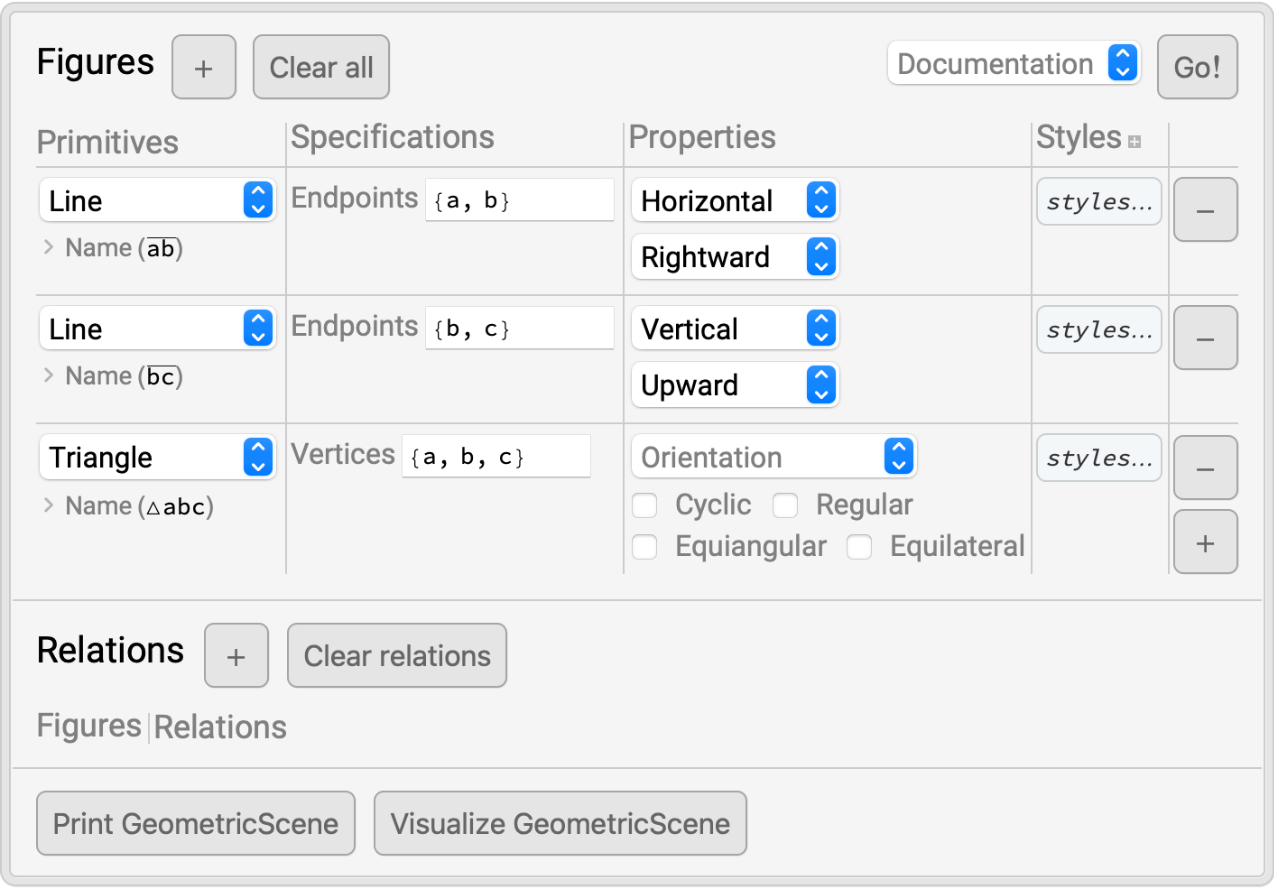
| In[6]:= | ![RandomInstance[
GeometricScene[{a, b, c}, {GeometricAssertion[Line[{a, b}], "Horizontal", "Rightward"], GeometricAssertion[Line[{b, c}], "Vertical", "Upward"], Triangle[{a, b, c}]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/0f2/0f291348-ccb5-49ec-a7a6-03d93a45ccb8/0c8251d5096a9c96.png) |
| Out[6]= | 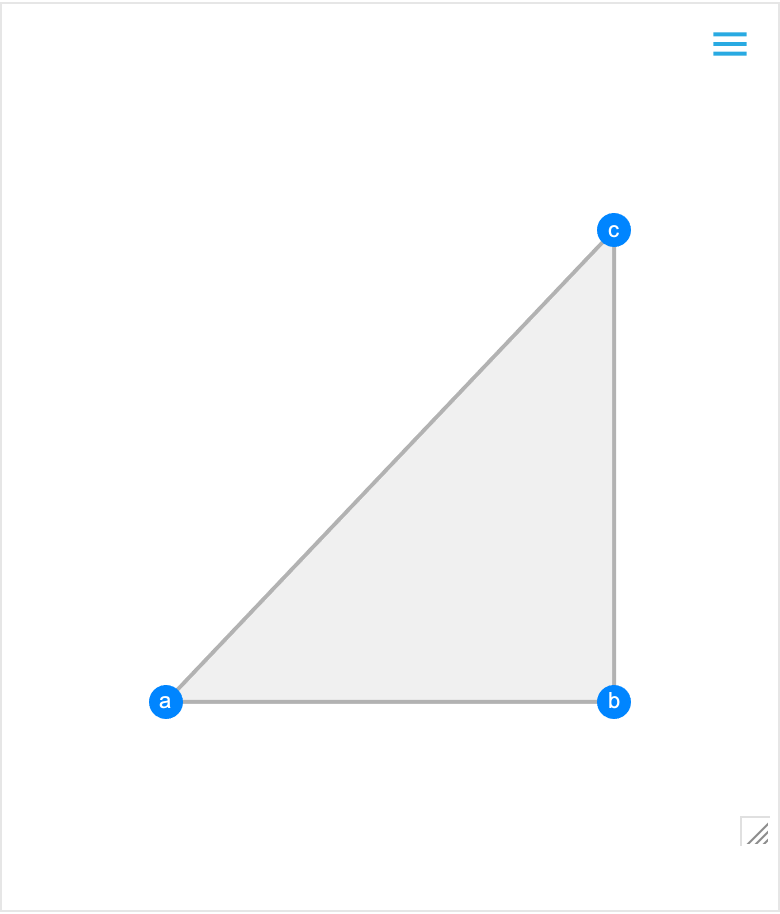 |
Construct scenes with constraints or conditions on the figures by introducing relations:
| In[7]:= |
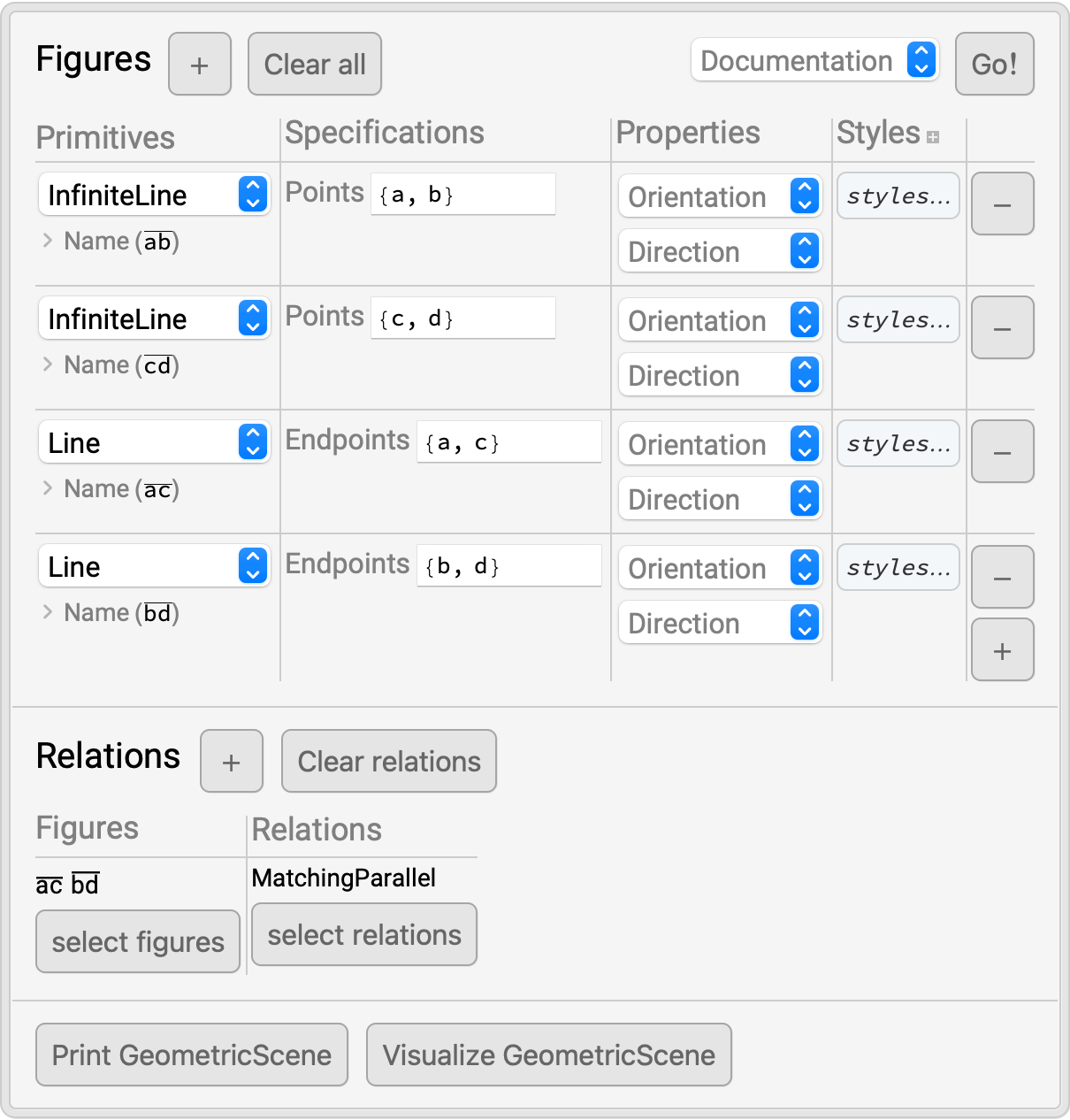
| In[8]:= | ![RandomInstance[
GeometricScene[{a, b, c, d}, {InfiniteLine[{a, b}], InfiniteLine[{c, d}], Line[{a, c}], Line[{b, d}], GeometricAssertion[{Line[{a, c}], Line[{b, d}]}, "MatchingParallel"]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/0f2/0f291348-ccb5-49ec-a7a6-03d93a45ccb8/3e84f47c548b3e91.png) |
| Out[8]= | 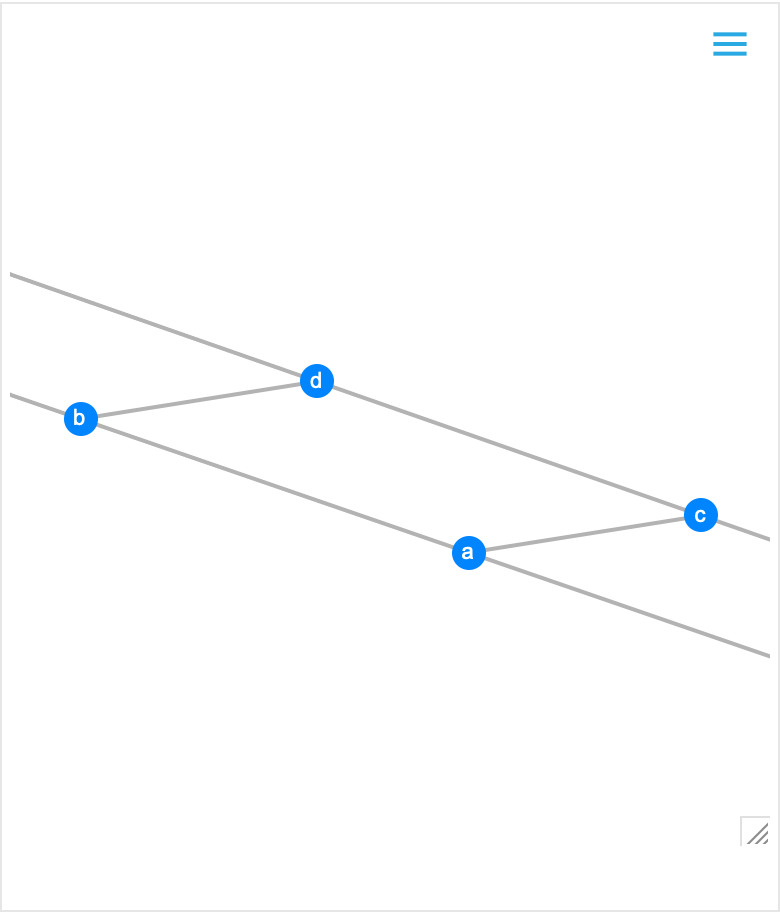 |
Click on the "Styles" column header to modify the appearance of elements in your scene:
| In[9]:= |
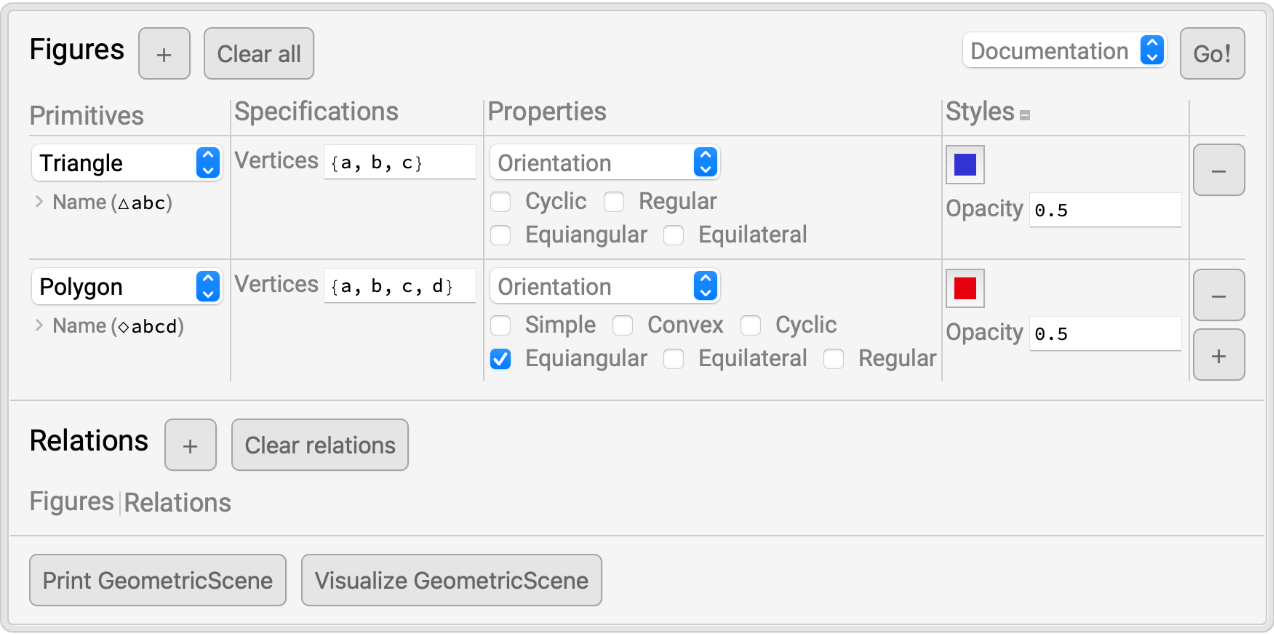
| In[10]:= | ![RandomInstance[
GeometricScene[{a, b, c, d}, {Style[Triangle[{a, b, c}], Directive[{RGBColor[
0.1970397497520409, 0.20027466239414055`, 0.8226596475165942], Opacity[0.5`]}]], GeometricAssertion[
Style[Polygon[{a, b, c, d}], Directive[{RGBColor[0.9031662470435645, 0., 0.04931715877012283],
Opacity[0.5`]}]], "Equiangular"]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/0f2/0f291348-ccb5-49ec-a7a6-03d93a45ccb8/232479221c1af3de.png) |
| Out[10]= | 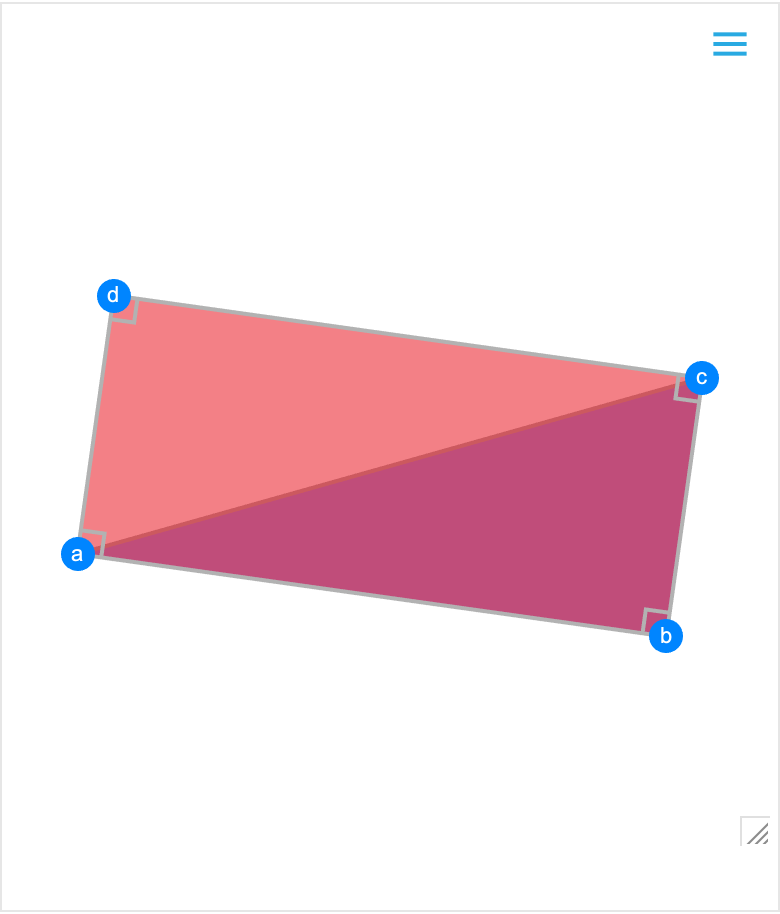 |
Construct a simple scene and visualize it:
| In[11]:= |
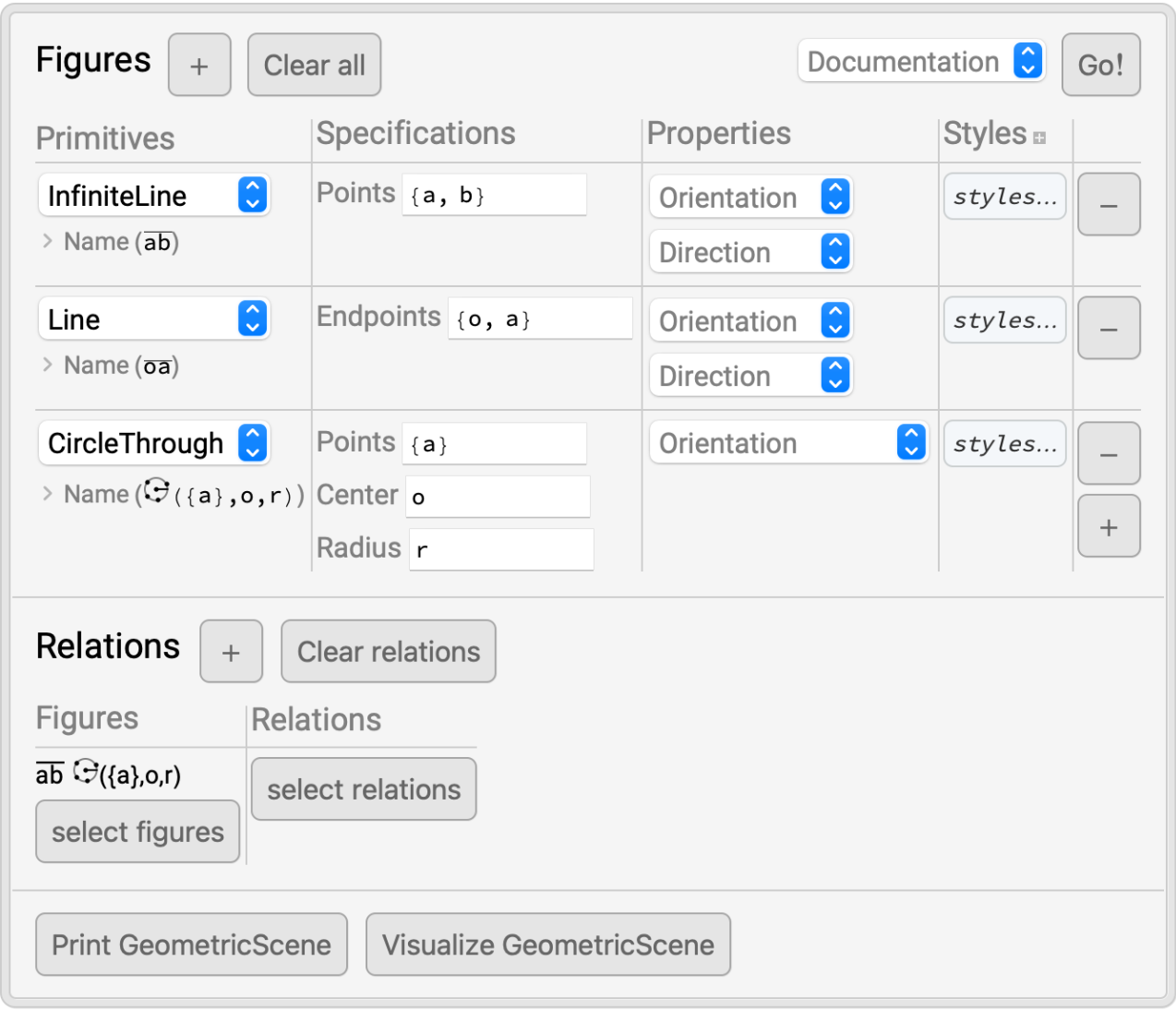
| In[12]:= | ![RandomInstance[
GeometricScene[{{a, b, o}, {r}}, {InfiniteLine[{a, b}], Line[{o, a}],
CircleThrough[{a}, o, r], GeometricAssertion[{InfiniteLine[{a, b}], CircleThrough[{a}, o, r]}, "Tangent"]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/0f2/0f291348-ccb5-49ec-a7a6-03d93a45ccb8/0352972e705f2c75.png) |
| Out[12]= | 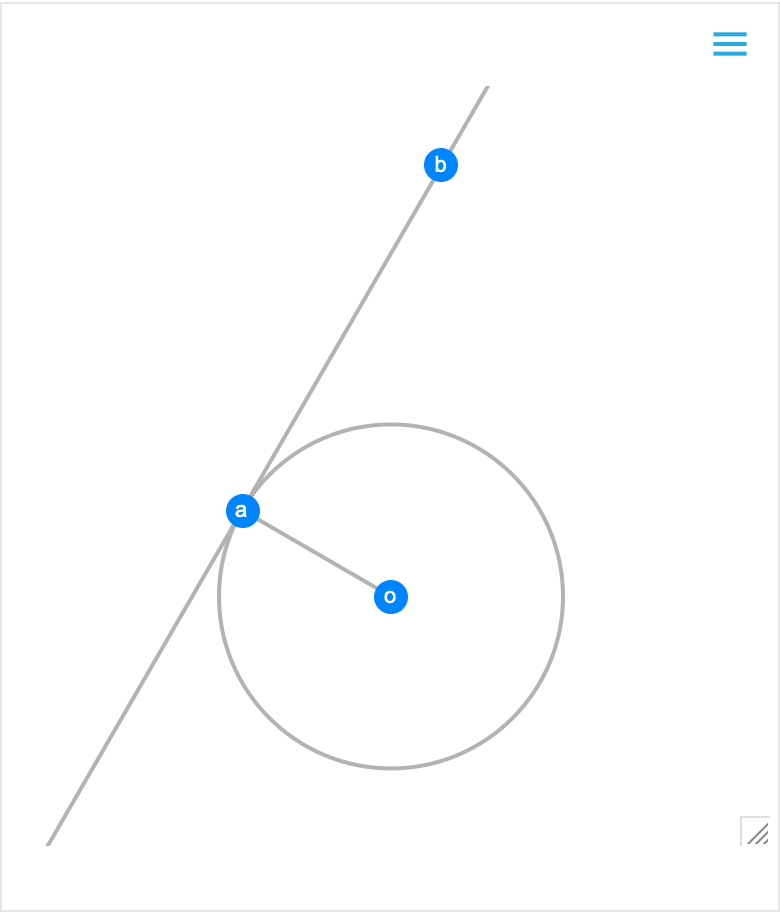 |
Then use FindGeometricConjectures to draw conclusions from the scene:
| In[13]:= |
| Out[13]= | 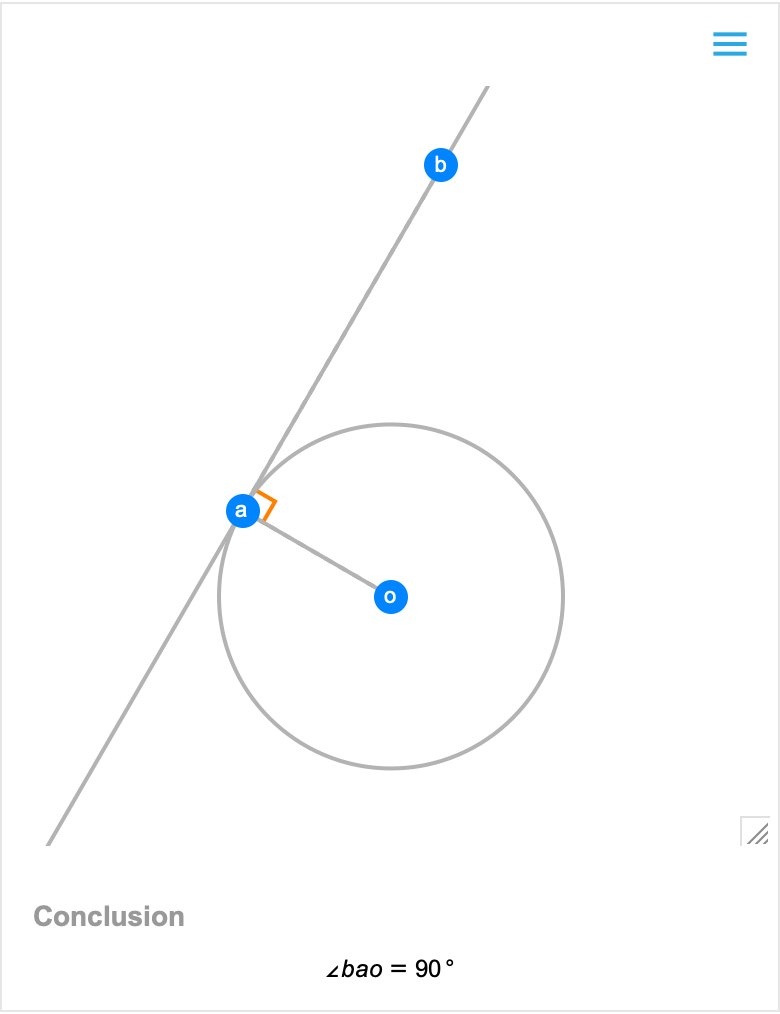 |
Construct a geometric scene with a numerical value for an angle:
| In[14]:= |
| In[15]:= | ![RandomInstance[
GeometricScene[{a, b, c, d}, {InfiniteLine[{a, b}], InfiniteLine[{c, d}], Line[{a, c}], Line[{b, d}], PlanarAngle[{a, b, d}] == \[Pi]/3, GeometricAssertion[{InfiniteLine[{a, b}], InfiniteLine[{c, d}]}, "MatchingParallel"], GeometricAssertion[{Line[{a, c}], Line[{b, d}]}, "Parallel"]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/0f2/0f291348-ccb5-49ec-a7a6-03d93a45ccb8/7e5927392ae10a9d.png) |
| Out[15]= | 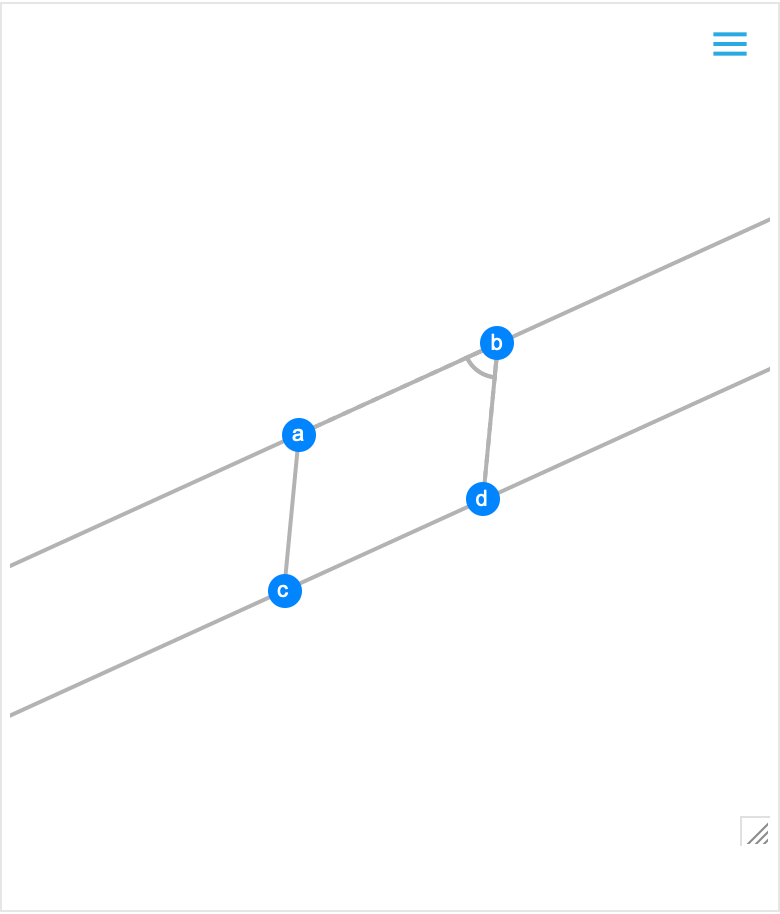 |
Use the resource function GeometricSolve to compute the numerical value of another angle from the scene and confirm that it is the same value as the opposite angle:
| In[16]:= |
| Out[16]= |
| In[17]:= |
| Out[17]= |
This work is licensed under a Creative Commons Attribution 4.0 International License