Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a geodesic dome from a polyhedral base
ResourceFunction["GeodesateMesh"][reg,n] generates a region representing the projection of the order-n regular tessellation of each face of the polyhedron reg onto the circumscribed sphere centered at the origin. | |
ResourceFunction["GeodesateMesh"][reg,n,p,r] uses a circumscribed sphere centered at the point p with radius r. |
Geodesate an icosahedron:
| In[1]:= |
| Out[1]= |  |
Use the default geodesation order:
| In[2]:= |
| Out[2]= |  |
Use a different center and radius for the circumscribing sphere:
| In[3]:= |
| Out[3]= | 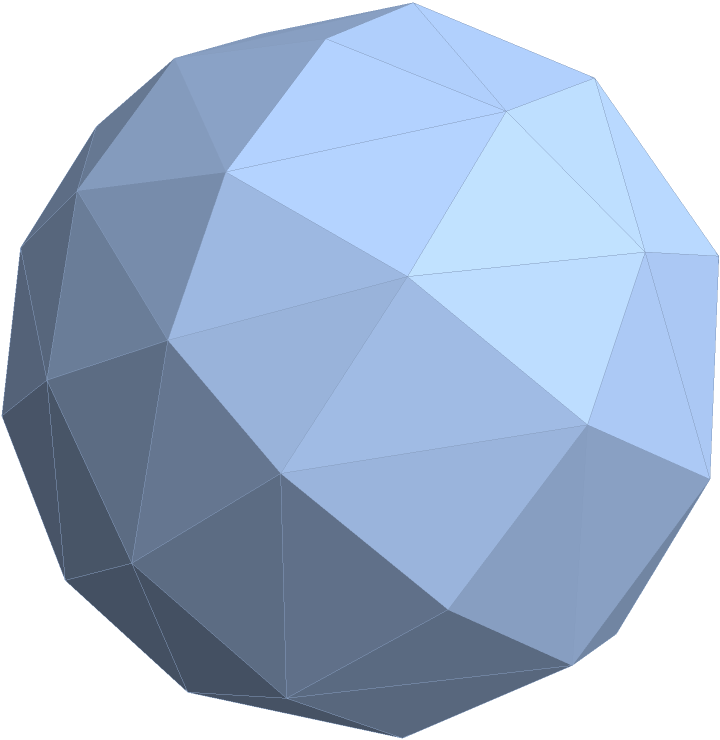 |
Use GeodesateMesh on a GraphicsComplex object:
| In[4]:= | ![Graphics3D[
ResourceFunction["GeodesateMesh"][
PolyhedronData["ElongatedTriangularGyrobicupola", "GraphicsComplex"], 3]]](https://www.wolframcloud.com/obj/resourcesystem/images/698/6984a241-2618-4d99-a173-e7b02e04342d/49955751c7b5d4ef.png) |
| Out[4]= | 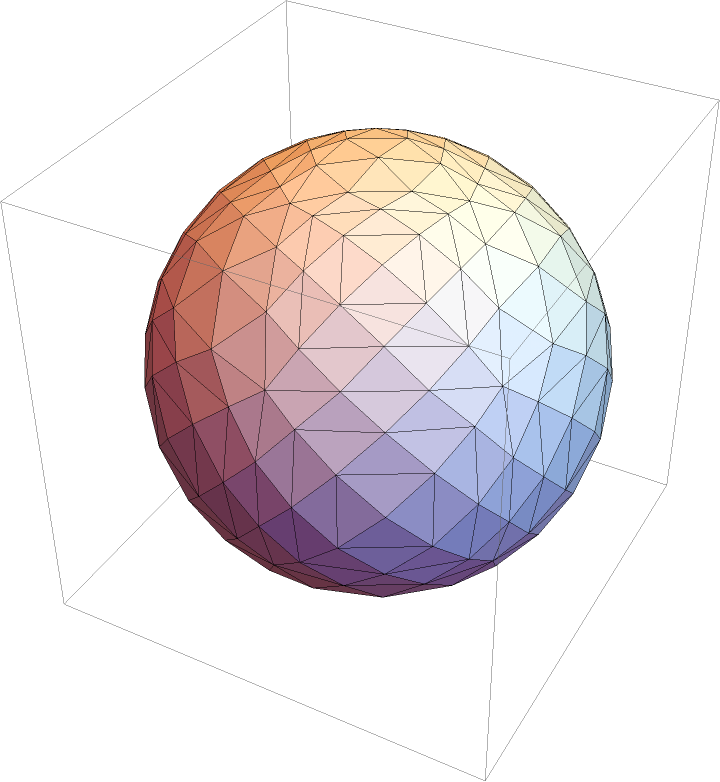 |
Use CanonicalizePolyhedron to get a Polyhedron object that can be used in Graphics3D:
| In[5]:= |
| Out[5]= | 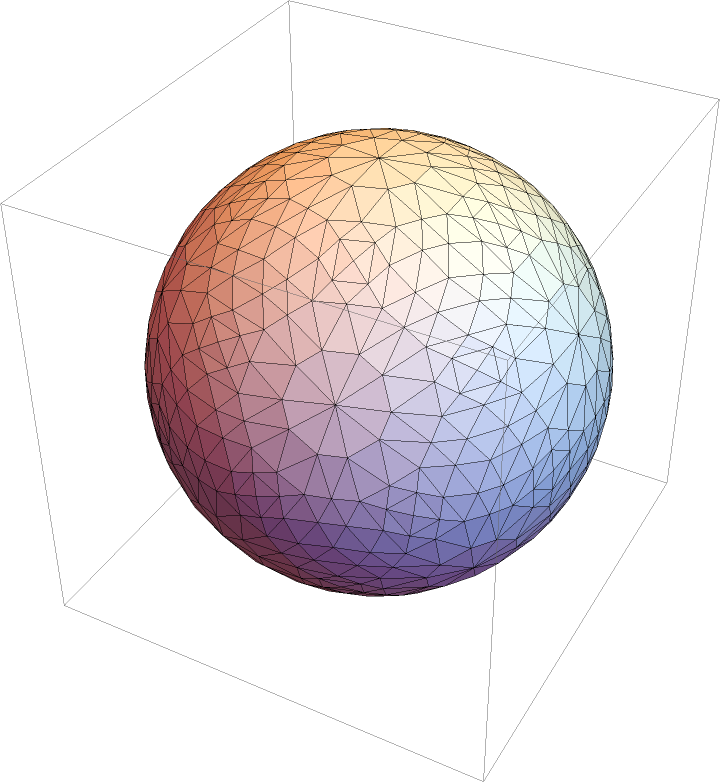 |
Visualize a Goldberg polyhedron:
| In[6]:= | ![DualPolyhedron[
CanonicalizePolyhedron[
ResourceFunction["GeodesateMesh"][
PolyhedronData["PentakisDodecahedron", "BoundaryMeshRegion"], 3]]] // Graphics3D](https://www.wolframcloud.com/obj/resourcesystem/images/698/6984a241-2618-4d99-a173-e7b02e04342d/62633a65fc875431.png) |
| Out[6]= | 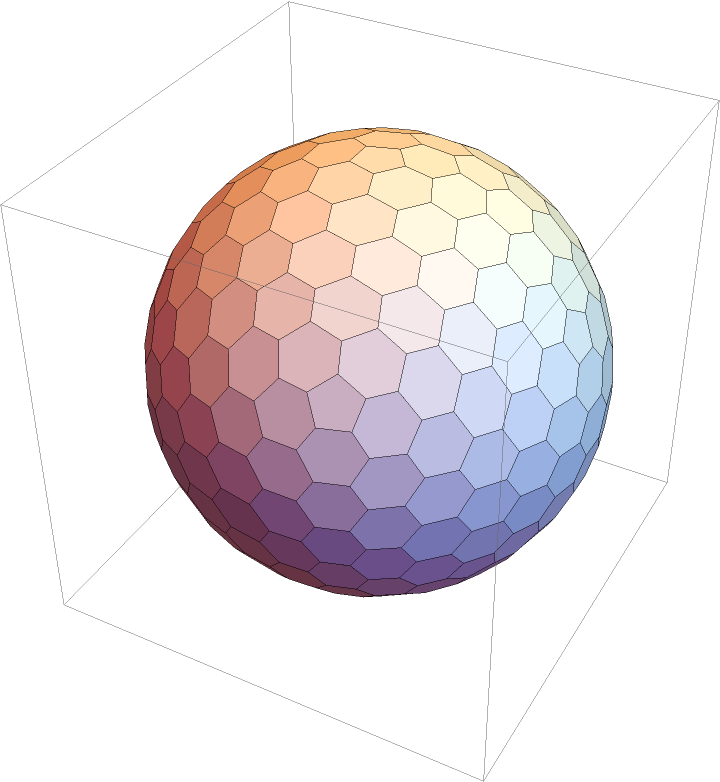 |
This work is licensed under a Creative Commons Attribution 4.0 International License