Basic Examples (2)
Find the successive distances between your location, Null Island, which is the area of ocean near Africa with 0 latitude and 0 longitude, the North and South Poles, and the antipode of your location:
Convert to kilometers:
Applications (13)
A megacity, according to the United Nations Department of Economic and Social Affairs, is an urban agglomeration with 10 million inhabitants. Compute the positions for a list of megacities:
Find the successive spatial distances for a list of megacities:
Compare with the result of GeoDistanceList:
Find the difference:
Find the average decrease in distance if you could travel through the Earth:
Find how fast it would take to travel this distance at the speed of light:
Find the shortest path starting and ending at the two closest megacities to your location:
Find the index of the cities:
Find the shortest tour of all mega-cities:
Compare the distances with GeoDistance over Earth's surface and GeoSpatialDistance through space:
Find the difference:
Evaluate how fast this would take to travel at the speed of light:
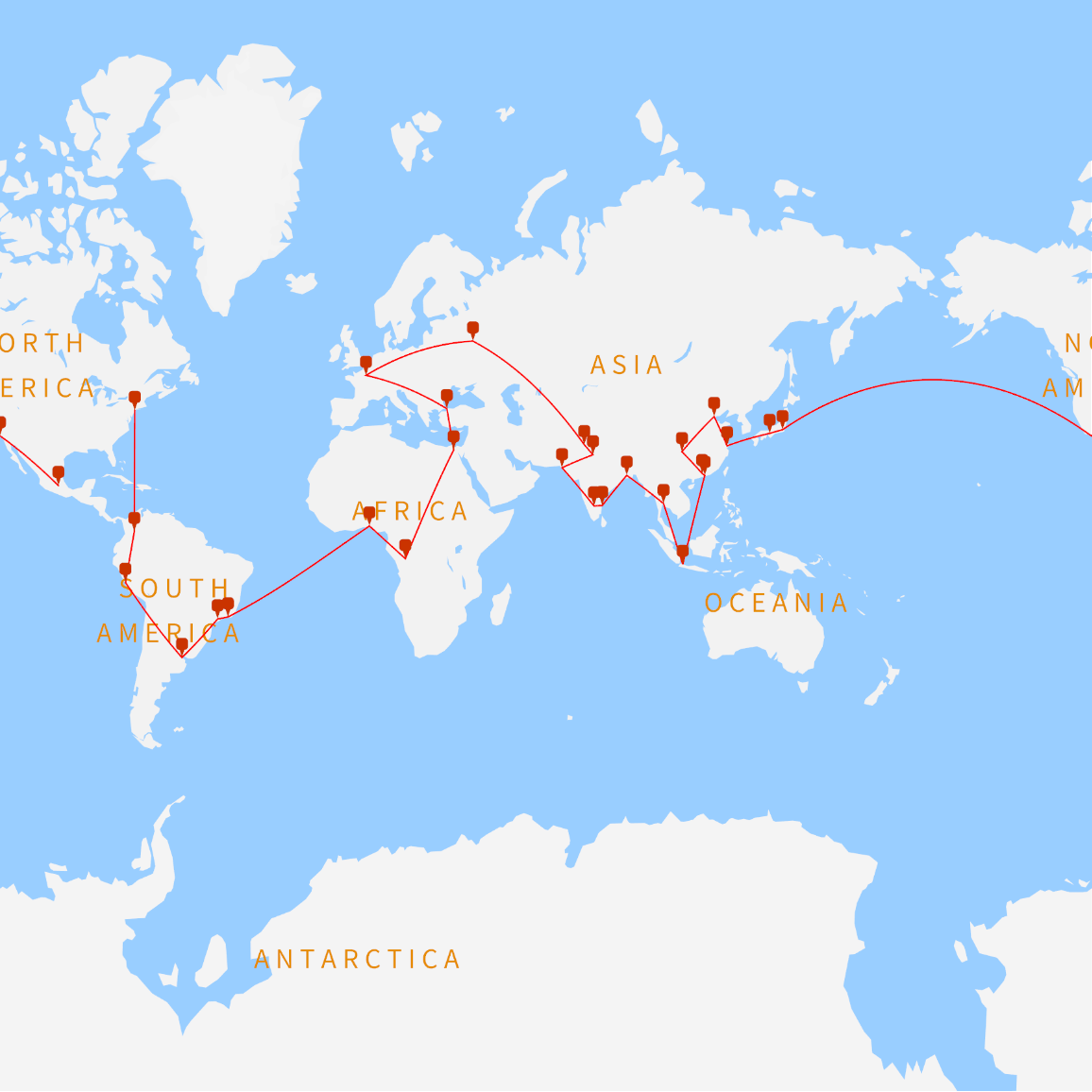
Make a map of the cities with geo markers for each city:
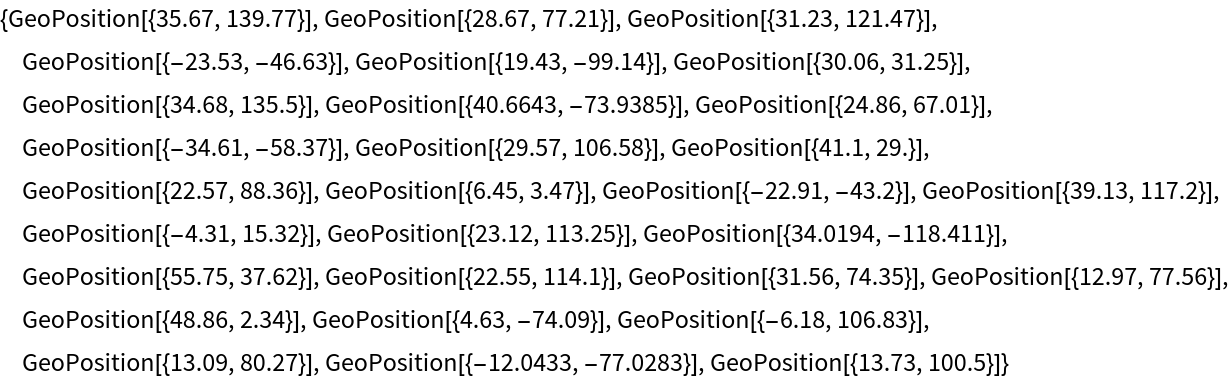
![megacities = {Entity["City", {"Tokyo", "Tokyo", "Japan"}], Entity["City", {"Delhi", "Delhi", "India"}], Entity["City", {"Shanghai", "Shanghai", "China"}], Entity["City", {"SaoPaulo", "SaoPaulo", "Brazil"}], Entity["City", {"MexicoCity", "DistritoFederal", "Mexico"}], Entity["City", {"Cairo", "Cairo", "Egypt"}], Entity["City", {"Osaka", "Osaka", "Japan"}], Entity["City", {"NewYork", "NewYork", "UnitedStates"}], Entity["City", {"Karachi", "Sind", "Pakistan"}], Entity["City", {"BuenosAires", "BuenosAires", "Argentina"}], Entity["City", {"Chongqing", "Chongqing", "China"}], Entity["City", {"Istanbul", "Istanbul", "Turkey"}], Entity["City", {"Calcutta", "WestBengal", "India"}], Entity["City", {"Lagos", "Lagos", "Nigeria"}], Entity["City", {"RioDeJaneiro", "RioDeJaneiro", "Brazil"}], Entity["City", {"Tianjin", "Tianjin", "China"}], Entity["City", {"Kinshasa", "Kinshasa", "DemocraticRepublicCongo"}], Entity["City", {"Guangzhou", "Guangdong", "China"}], Entity["City", {"LosAngeles", "California", "UnitedStates"}], Entity["City", {"Moscow", "Moscow", "Russia"}], Entity["City", {"Shenzhen", "Guangdong", "China"}], Entity["City", {"Lahore", "Punjab", "Pakistan"}], Entity["City", {"Bengaluru", "Karnataka", "India"}], Entity["City", {"Paris", "IleDeFrance", "France"}], Entity["City", {"Bogota", "DistritoCapital", "Colombia"}], Entity["City", {"Jakarta", "Jakarta", "Indonesia"}], Entity["City", {"Madras", "TamilNadu", "India"}], Entity["City", {"Lima", "Lima", "Peru"}], Entity["City", {"Bangkok", "Bangkok", "Thailand"}]};](https://www.wolframcloud.com/obj/resourcesystem/images/ece/eceee46d-d7cb-4d22-9623-4ab8b817384e/0f851ae81d13dabe.png)


![UnitConvert[ResourceFunction["GeoSpatialDistanceList"][positions], "SI"] - Normal[UnitConvert[GeoDistanceList[positions], "SI"]]](https://www.wolframcloud.com/obj/resourcesystem/images/ece/eceee46d-d7cb-4d22-9623-4ab8b817384e/1add17a553e4d5c3.png)

![Mean[UnitConvert[
ResourceFunction["GeoSpatialDistanceList"][positions], "SI"] - Normal[UnitConvert[GeoDistanceList[positions], "SI"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/ece/eceee46d-d7cb-4d22-9623-4ab8b817384e/7148e30742f0ddf7.png)
![UnitSimplify[
Mean[UnitConvert[
ResourceFunction["GeoSpatialDistanceList"][positions], "SI"] - Normal[UnitConvert[GeoDistanceList[positions], "SI"]]]/
Quantity["SpeedOfLight"]]](https://www.wolframcloud.com/obj/resourcesystem/images/ece/eceee46d-d7cb-4d22-9623-4ab8b817384e/5b88f4a5ff1ac9a5.png)
![spatialdistance = Quantity[
First[FindShortestTour[positions, 8, 5, DistanceFunction -> (QuantityMagnitude[
ResourceFunction["GeoSpatialDistance"][#1, #2]] &)]], "Kilometers"]](https://www.wolframcloud.com/obj/resourcesystem/images/ece/eceee46d-d7cb-4d22-9623-4ab8b817384e/1dabe6ae3094a2e6.png)
![GeoGraphics[{{Thick, Red, GeoPath[positions[[{
Quantity[61590.728145031404`, "Kilometers"], {8, 25, 28, 10, 4, 15, 14, 17, 6, 12, 24, 20, 22, 2, 9, 23, 27, 13, 29, 26, 21, 18, 11, 16, 3, 7, 1, 19, 5}}[[2]]]]]}, GeoMarker[positions, "Scale" -> 4]}, GeoBackground -> "VectorBusiness"]](https://www.wolframcloud.com/obj/resourcesystem/images/ece/eceee46d-d7cb-4d22-9623-4ab8b817384e/0bdeedfd789fe8cb.png)