Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GenericInvariant

Source Notebook

Compute the generic invariant of a group

Contributed by: Tessa Wildsmith and Enrique Zeleny

ResourceFunction["GenericInvariant"][gr]

computes the generic invariant of a group gr of the same order as the group order.

ResourceFunction["GenericInvariant"][gr,n]

computes the generic invariant of a group gr of order n, greater than or equal to the group order.

Details

Let G be a subgroup of the symmetric group Sn of permutations of n elements. A polynomial invariant of G is a polynomial expression I∈K [X1,x2,…,Xn] which is left unchanged under a given set of algebraic transformations, namely the permutations of a given group G. In other words: for every σ∈G, I(xσ(1)…xσ(n)) = I(x1,…,xn).
The computation of the Galois group of a polynomial requires a priori knowledge of the invariant functions that correspond to subgroups of Sn, hence reducing these invariants shall optimise the isolation of the Galois group. Let F*(x1,x2,…,xn)=x1x2…xn. Then define our function to be .
In the Stauduhar method, the invariant functions F that are used to isolate integer roots to the resolvent polynomial (a polynomial of lower degree whose roots are related to the roots of the original polynomial) of a given group.

Examples

Basic Examples (3) 

Generic invariant of a permutation group:

In[1]:=
pc = PermutationGroup[{Cycles[{{1, 3, 2, 5, 4}}]}];
In[2]:=
ResourceFunction["GenericInvariant"][pc, 5]
Out[2]=

An equivalent specification:

In[3]:=
ResourceFunction["GenericInvariant"][pc, Range[5]]
Out[3]=

Using literals:

In[4]:=
ResourceFunction["GenericInvariant"][pc, {a, b, c, d, e}]
Out[4]=
In[5]:=
Expand[%]
Out[5]=

Scope (2) 

Generic invariant of a symmetric group:

In[6]:=
ResourceFunction["GenericInvariant"][SymmetricGroup[4], 4]
Out[6]=

The generic invariant can grow in size very quickly:

In[7]:=
ResourceFunction["GenericInvariant"][ PermutationGroup[{Cycles[{{5, 10}}], Cycles[{{1, 3, 5, 7, 9}, {2, 4, 6, 8, 10}}], Cycles[{{2, 4, 10}, {5, 7, 9}}]}], 10]
Out[7]=

Properties and Relations (1) 

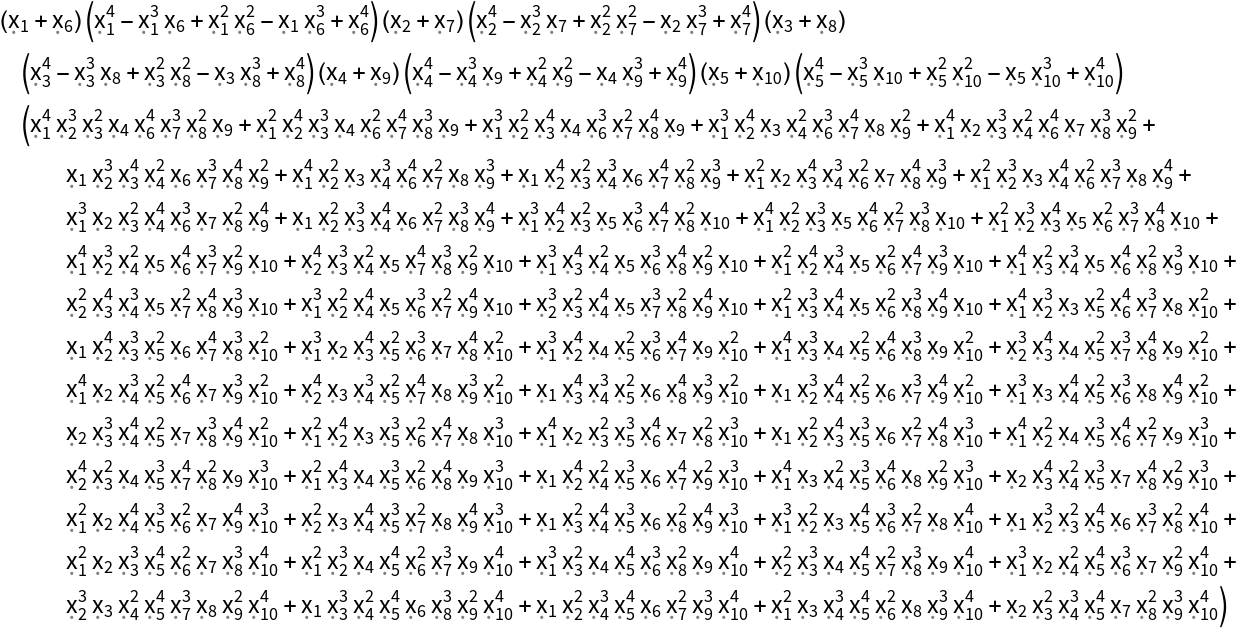Get the generic invariant of a polynomial using Stauduhar's method:

In[8]:=
ResourceFunction["StauduharGaloisGroup"][ x^4 + 7 x \[Minus] 7, x, "GaloisGroup"]
Out[8]=
In[9]:=
ResourceFunction["GenericInvariant"][%, 4]
Out[9]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 31 January 2022

Source Metadata

Related Resources

License Information