Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GenerateWangTiling

Source Notebook

Generate a tiling pattern from a set of Wang tiles

Contributed by: Bradley Klee

ResourceFunction["GenerateWangTiling"][tiles,{},n]

covers an n× n array with edge-matching Wang tiles.

ResourceFunction["GenerateWangTiling"][tiles,{},{m,n}]

covers an m× n array instead.

ResourceFunction["GenerateWangTiling"][tiles,{},size,All]

lists all array coverings consistent with edge matching rules of the tiles.

ResourceFunction["GenerateWangTiling"][tiles,{},size,count]

lists multiple coverings, up to integer count of them.

ResourceFunction["GenerateWangTiling"][tiles,seed,size,count]

forces the seed tile to occur near the center of the pattern.

Details

Generally, a Wang tile is a square whose South, East, North, and West edges are labeled with a matching color.
Two adjacent Wang tiles match on either North / South or East / West boundary when they have the same matching color on their shared edge.
Often matching colors are represented by numbers or more generally symbols. Here we prefer to use non-negative integers.
Input tiles should list a set of Wang tiles, each encoded as list of exactly four non-negative integers.
The four matching symbols are assumed to have a counter-clockwise order on square edges: SENW.
Here we call any rectangular array of Wang tiles a tiling pattern.
An “admissible” tiling pattern is one whose shared edges also share the same matching symbols.
ResourceFunction["GenerateWangTiling"] assumes that possible edge values in a tiling pattern are bounded above by the maximum integer found in the set of tiles.
ResourceFunction["GenerateWangTiling"] takes one Option "Boundary". When set to "Periodic", ResourceFunction["GenerateWangTiling"] also requires edge matching across North-South and East-West edges (i.e. toroidal boundary conditions).

Examples

Basic Examples (2) 

Generate part of a Wang tiling from a set of just one tile:

In[1]:=
ResourceFunction["GenerateWangTiling"][{{0, 1, 0, 1}}, {}, 3]
Out[1]=

Depict the 3×3 tiling as a Graphics object:

In[2]:=
With[{wangGraphics = Function[{or, tile, colRules}, MapThread[{#, EdgeForm[Black], Polygon[ Append[ Map[or + #& , #2], or]]}& , { ReplaceAll[ tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]]}, Show[#, ImageSize -> 150] &@MapIndexed[ Graphics@wangGraphics[ Reverse[#2 {-1, 1}], #1, {0 -> Lighter[Red], 1 -> Lighter[Gray]}] &, #, {2}] &@ResourceFunction["GenerateWangTiling"][ {{0, 1, 0, 1}}, {}, 3]]
Out[2]=

Change the region size to 2×4:

In[3]:=
With[{wangGraphics = Function[{or, tile, colRules}, MapThread[{#, EdgeForm[Black], Polygon[ Append[ Map[or + #& , #2], or]]}& , { ReplaceAll[ tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]]}, Show[#, ImageSize -> 200] &@MapIndexed[ Graphics@wangGraphics[ Reverse[#2 {-1, 1}], #1, {0 -> Lighter[Red], 1 -> Lighter[Gray]}] &, #, {2}] &@ResourceFunction["GenerateWangTiling"][ {{0, 1, 0, 1}}, {}, {2, 4}]]
Out[3]=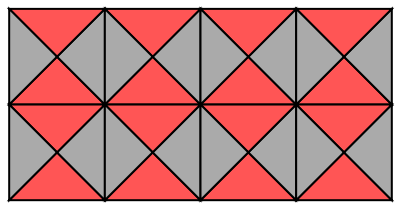

Plot a periodic pattern by alternating between two Wang tiles:

In[4]:=
With[{wangGraphics = Function[{or, tile, colRules}, MapThread[{#, EdgeForm[Black], Polygon[ Append[ Map[or + #& , #2], or]]}& , { ReplaceAll[ tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]], cols = {1 -> RGBColor[1, 0.75, 0], 2 -> RGBColor[0., 1., 0.5], 3 -> RGBColor[0.5, 0.5, 1.], 4 -> RGBColor[1., 0.4, 0.85]}}, Show[#, ImageSize -> 200] &@MapIndexed[ Graphics@wangGraphics[ Reverse[#2 {-1, 1}], #1, cols] &, #, {2}] &@ResourceFunction["GenerateWangTiling"][ {{1, 3, 2, 4}, {2, 4, 1, 3}}, {1, 3, 2, 4}, 4]]
Out[4]=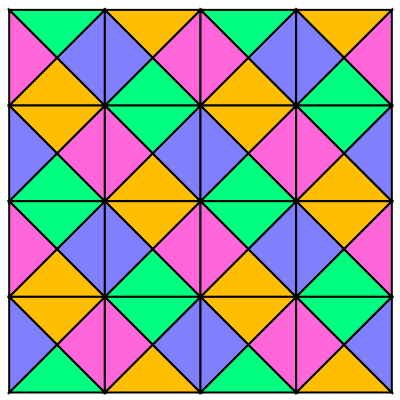

Shift the pattern's offset by changing the seed tile:

In[5]:=
With[{wangGraphics = Function[{or, tile, colRules}, MapThread[{#, EdgeForm[Black], Polygon[ Append[ Map[or + #& , #2], or]]}& , { ReplaceAll[ tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]], cols = {1 -> RGBColor[1, 0.75, 0], 2 -> RGBColor[0., 1., 0.5], 3 -> RGBColor[0.5, 0.5, 1.], 4 -> RGBColor[1., 0.4, 0.85]}}, Show[#, ImageSize -> 200] &@MapIndexed[ Graphics@wangGraphics[ Reverse[#2 {-1, 1}], #1, cols] &, #, {2}] &@ResourceFunction["GenerateWangTiling"][ {{1, 3, 2, 4}, {2, 4, 1, 3}}, {2, 4, 1, 3}, 4]]
Out[5]=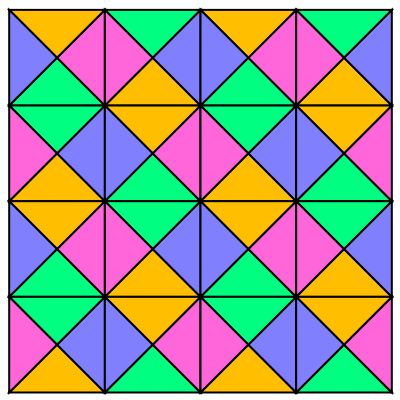

Verify that this tiling pattern in four colors has only two translates:

In[6]:=
Length@ResourceFunction["GenerateWangTiling"][{{1, 3, 2, 4}, {2, 4, 1, 3}}, {}, 4, All]
Out[6]=

Scope (1) 

GenerateWangTiling can get returns for bigger tile sets with more colors:

In[7]:=
With[{cols = MapIndexed[# -> Lighter[Hue[#2[[1]]/18], .5] &, Flatten[Transpose[Partition[Range[16], 2]]]], wangGraphics = Function[{or, tile, colRules}, MapThread[{#, EdgeForm[Black], Polygon[ Append[ Map[or + #& , #2], or]]}& , { ReplaceAll[ tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]], penroseTiles = {{1, 5, 3, 1}, {7, 2, 3, 1}, {1, 5, 12, 9}, {7, 2, 12, 9}, {1, 7, 12, 11}, {1, 4, 10, 16}, {1, 14, 6, 11}, {7, 10, 6, 9}, {2, 2, 4, 6}, {8, 2, 4, 1}, {2, 10, 11, 6}, {8, 10, 11, 1}, {2, 12, 11, 8}, {2, 15, 9, 3}, {2, 12, 5, 13}, {8, 10, 5, 9}, {4, 3, 2, 7}, {4, 3, 8, 4}, {10, 11, 2, 7}, {10, 11, 8, 4}, {10, 9, 2, 5}, {12, 13, 2, 2}, {5, 9, 2, 15}, {5, 11, 8, 12}, {3, 8, 1, 4}, { 3, 3, 7, 4}, {9, 8, 1, 12}, {9, 3, 7, 12}, {9, 6, 1, 10}, {11, 1, 1, 14}, {6, 16, 1, 10}, {6, 11, 7, 12}}}, Labeled[Show[#, ImageSize -> 600] &@MapIndexed[ Graphics@wangGraphics[ Reverse[#2 {-1, 1}], #1, cols] &, #, {2}] &@ResourceFunction["GenerateWangTiling"][ penroseTiles, {}, 20], Grid[Partition[Graphics[wangGraphics[{0, 0}, #, cols], ImageSize -> 30] & /@ penroseTiles, 16]]]]
Out[7]=

Options (1) 

GenerateWangTiling can also check boundary conditions:

In[8]:=
ResourceFunction["GenerateWangTiling"][ {{1, 3, 2, 4}, {2, 4, 1, 3}}, {}, #, All, "Boundary" -> "Periodic"] /. { x_List :> Length[x]} & /@ Range[3, 6]
Out[8]=

Neat Examples (1) 

Plot a section of the minimal-known aperiodic Wang tiling:

In[9]:=
With[{JeandelRaoTiles = {{1, 0, 0, 0}, {1, 2, 0, 2}, {2, 3, 1, 0}, {1, 0, 1, 3}, {1, 1, 1, 3}, {3, 3, 1, 3}, {2, 0, 2, 1}, {0, 1, 2, 1}, {0, 2, 2, 2}, {2, 1, 2, 3}, {2, 3, 3, 1}}, cols = {1 -> RGBColor[1., 0.4, 0.85], 2 -> RGBColor[0.5, 0.5, 1.], 3 -> RGBColor[1, 0.75, 0], 0 -> GrayLevel[0.85]}, wangGraphics = Function[{or, tile, colRules}, MapThread[{#, EdgeForm[Black], Polygon[ Append[ Map[or + #& , #2], or]]}& , { ReplaceAll[ tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]]}, Labeled[Show[#, ImageSize -> 600] &@MapIndexed[ Graphics@wangGraphics[ Reverse[#2 {-1, 1}], #1, cols] &, #, {2}] &@ResourceFunction["GenerateWangTiling"][ JeandelRaoTiles, {}, 20], Row[Graphics[wangGraphics[{0, 0}, #, cols], ImageSize -> 30] & /@ JeandelRaoTiles, Spacer[3]]]]
Out[9]=

Publisher

Brad Klee

Version History

  • 1.0.0 – 23 June 2022

Related Resources

License Information