Basic Examples (1)
Order three symbolic expressions involving the variables a and b:
Scope (2)
The expressions can contain constants:
Restrict the domain of permissible solutions:
Options (10)
Pattern (2)
Determine the conditions under which a−b will lie in the middle of the two other values:
Determine the conditions under which the ordering of a four-element list with respect to an operation will have its fourth member first and its second member third:
PatternInterpreter (2)
By setting the "PatternRepresentation" option, you can change the interpretation of the value of the "Pattern" option. For a value f taken by this option, and a value explist of the expressions to be sorted, the value of the "Pattern" option pat is interpreted as f[explist][pat]. Interpret the value of the "Pattern" option as indices into the list of expressions:
Use integer indices to represent a desired ordering but also permit blank patterns where one does not care about the exact ordering:
KeyFunction (2)
Represent the keys not as the expressions themselves but by indices into the original expression list:
Any arbitrary expression can be used as a "KeyFunction":
The default value for "KeyFunction" is Identity:
One can combine the "KeyFunction" option with the "Pattern" and "PatternInterpretation" functions:
AdditionalConstraint (4)
Place additional constraints on the expressions to be sorted:
The additional constraints can be geometric:
The additional constraints can result from the computation of an ImplicitRegion:
The additional constraints can result from the computation of a ParametricRegion:
All the options for Reduce are also supported, including user-specified generated parameters and display of full cubic and quartic expressions instead of root objects. The GeneratedParameters option works:
The Quartics option works (as does Cubics):
The WorkingPrecision option can be used:
Applications (2)
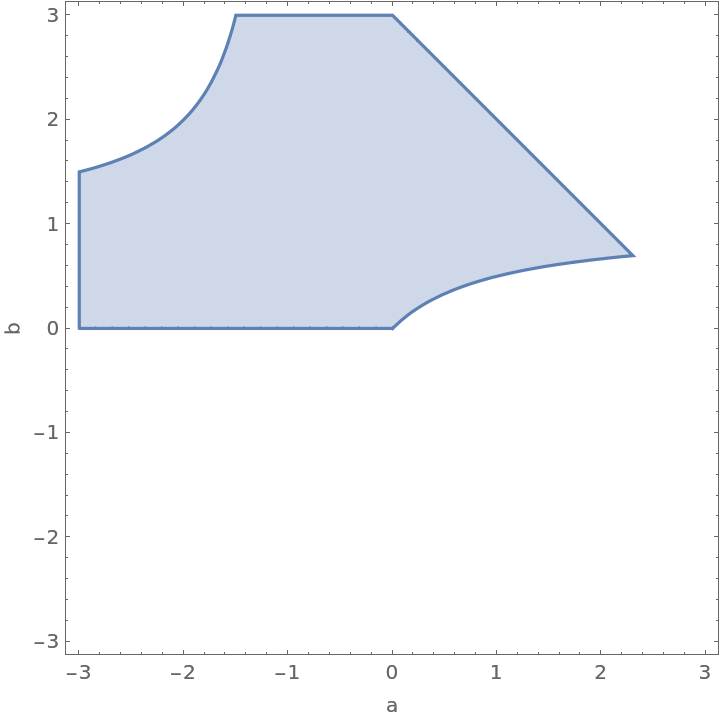
Show conditions under which a-b will have the smallest value among {a+b,a−b,a b}, but also requiring a+b<3:
In a three-party race, the first candidate has 20 votes, the second candidate has 25 votes, and the third candidate has 27 votes. It is estimated, however, that only 70% of the votes have been counted. Compute the conditions under which candidate 1 will end up with the most votes:
Plot the corresponding region:
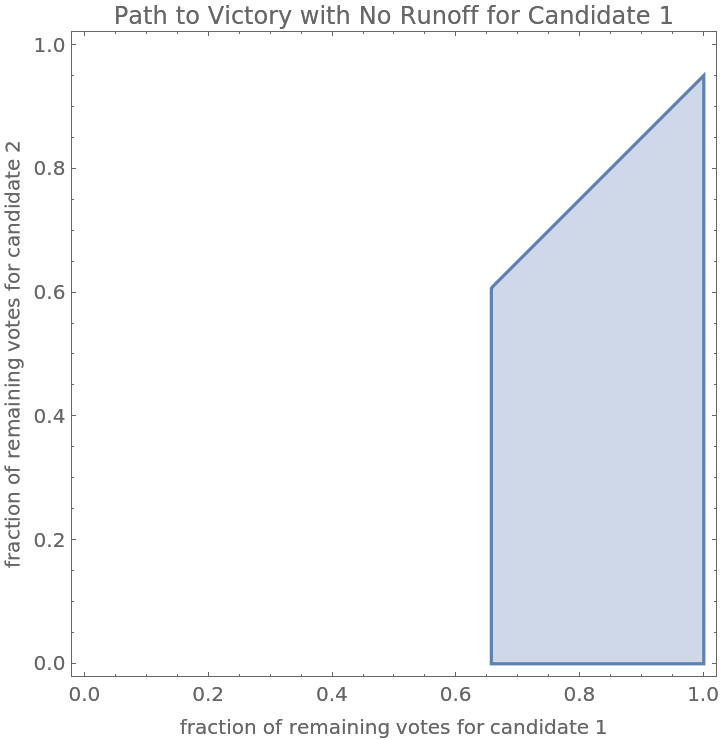
Do the same computation but assume that to avoid a runoff election, candidate 1 must get more than 50% of the total votes:
Plot the resulting region:
Possible Issues (3)
The "Modulus" option cannot be used if the op argument generates an inequality:
As the length of the expression list grows or the length of the vars argument grows, the time needed to do the computations can grow significantly:
If Reduce cannot determine the order of the expressions, the computation can take a long time:
Neat Examples (3)
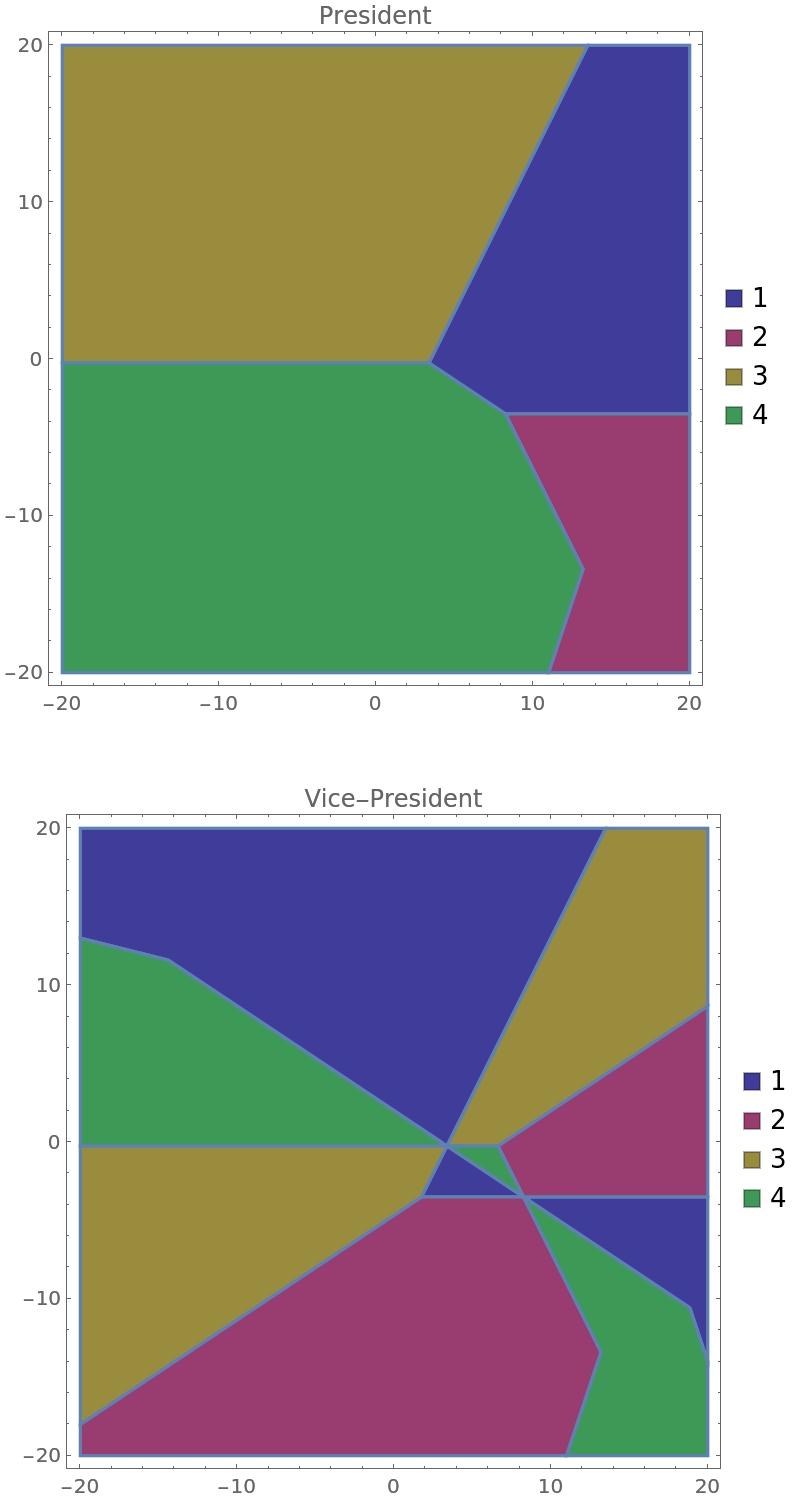
Under the original Article II of the United States Constitution and prior to the enactment of the Twelfth Amendment, the presidential candidate with the most votes in the electoral college would become the President of the United States and the candidate with the second-most votes would become the Vice President, even if the President and Vice President had serious disagreements. Suppose the electoral college votes of four candidates subject to that voting system depend on two parameters, x and y. Compute the conditions for each ordering of the four candidates:
Plot the regions of x and y for which each candidate becomes President and Vice President:
Compute the probability that each candidate will become President and Vice President, assuming that x and y are drawn from a multivariate normal distribution:
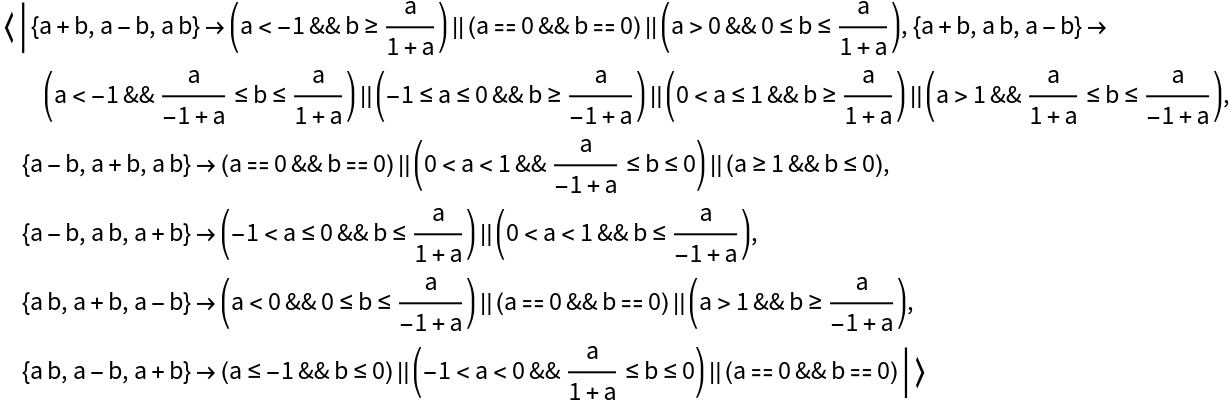
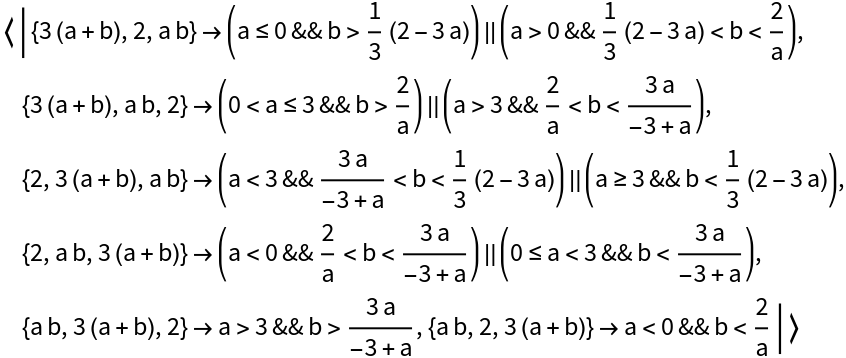
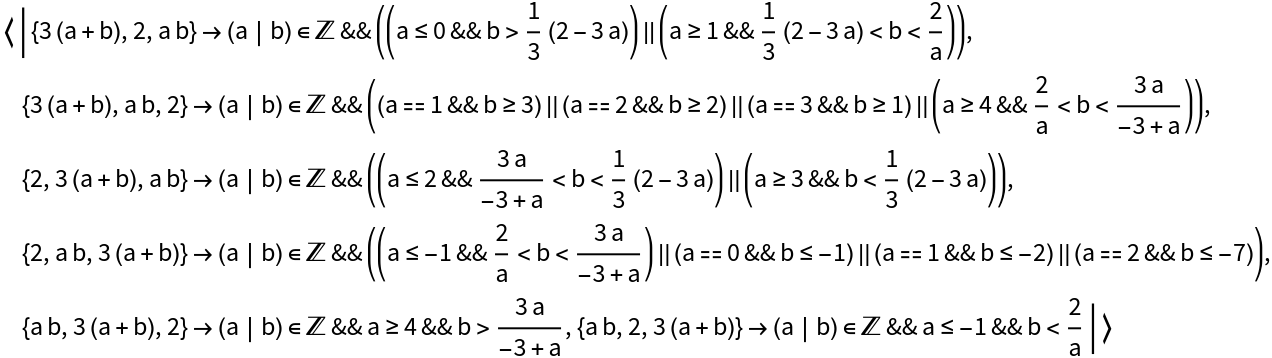
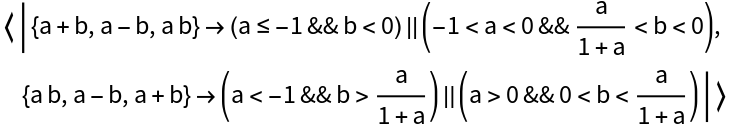
![Module[{augmentedexplist = Append[explist, a^3 - b^2], pat},
pat = Normal@
SparseArray[{1 -> augmentedexplist[[4]], 3 -> augmentedexplist[[2]]}, 4, _];
ResourceFunction["GenerateOrderingConditions"][Less, augmentedexplist, {a, b}, "Pattern" -> pat]]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/61696e80c5a3a325.png)

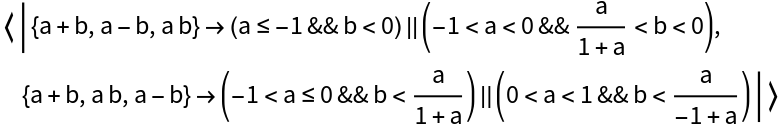
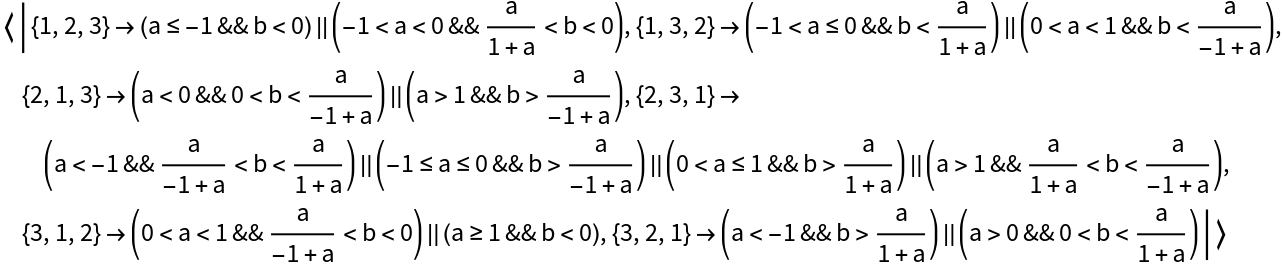
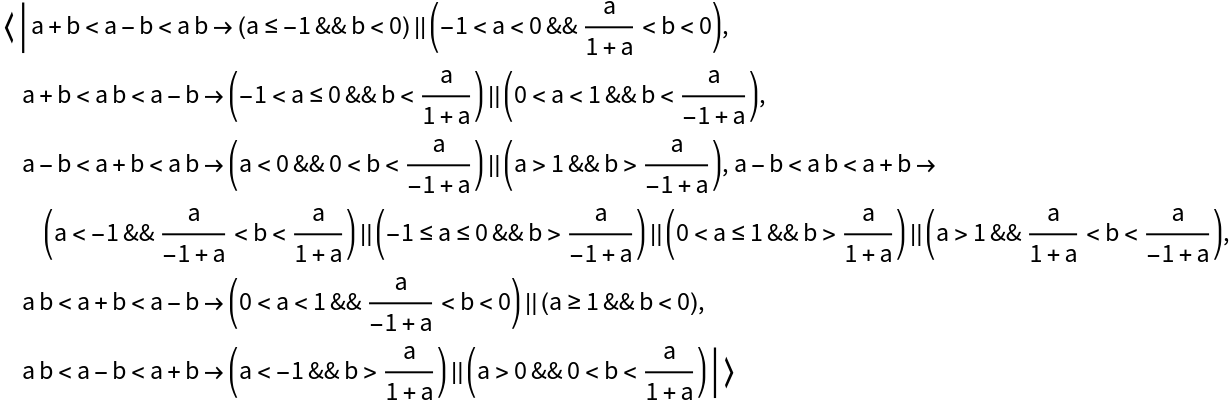
![ResourceFunction["GenerateOrderingConditions"][Less, explist, {a, b}, Integers, "KeyFunction" -> Identity] === ResourceFunction["GenerateOrderingConditions"][Less, explist, {a, b},
Integers]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/574883ec364538d1.png)
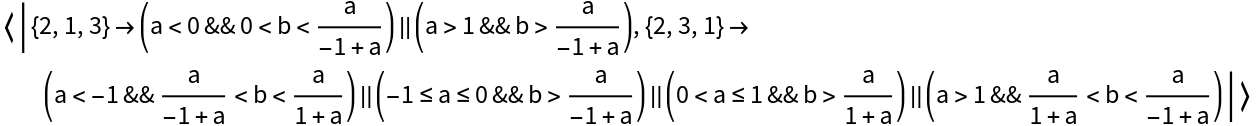
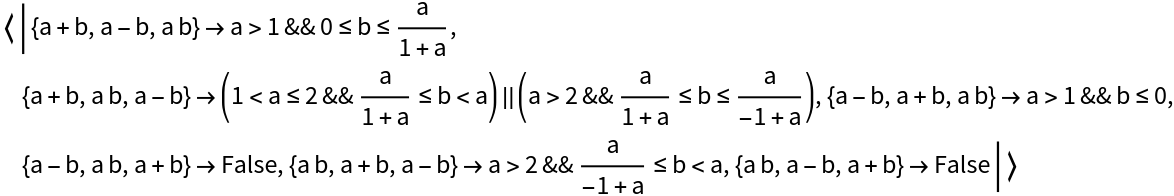
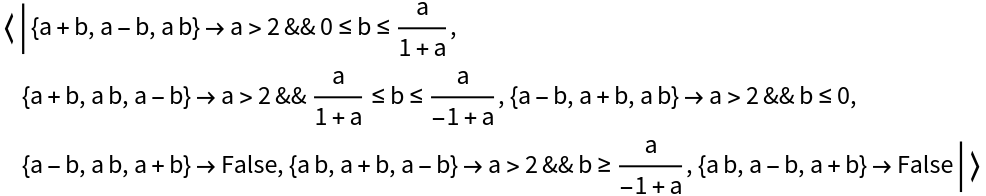

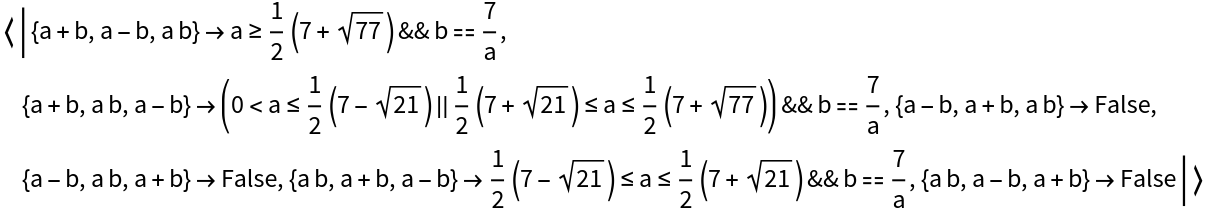
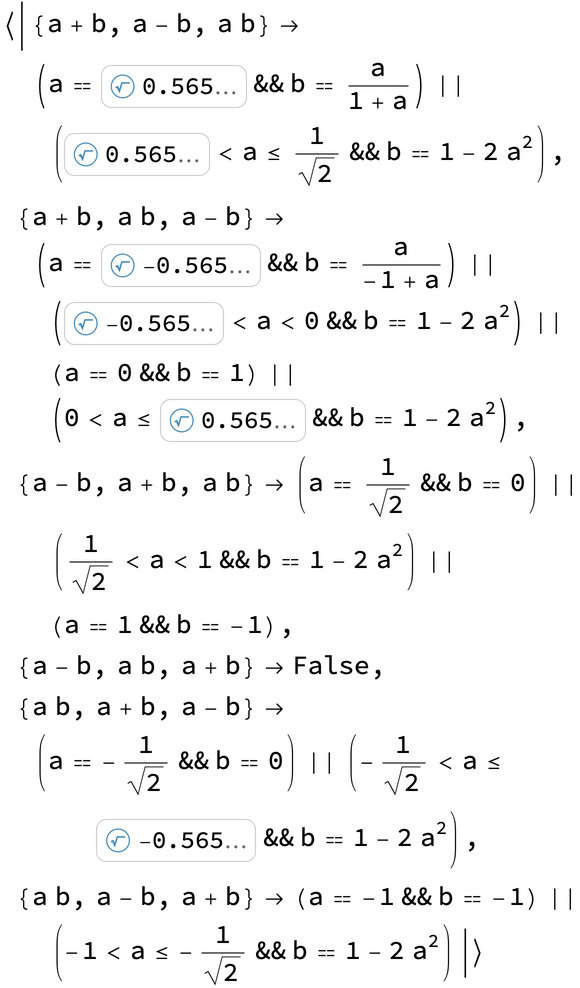
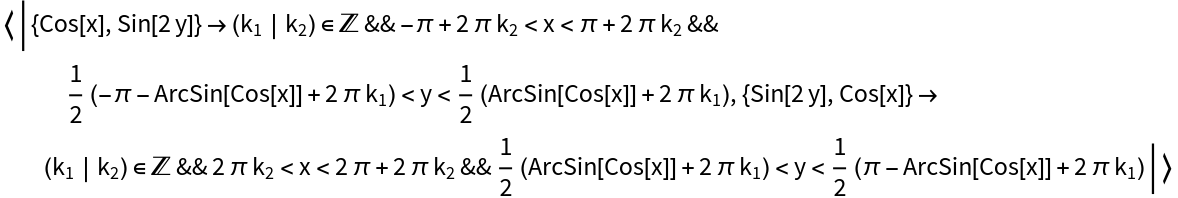
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/42523335-5c0d-4640-bab4-968223ed028d"]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/4e12facfc1a8cf16.png)
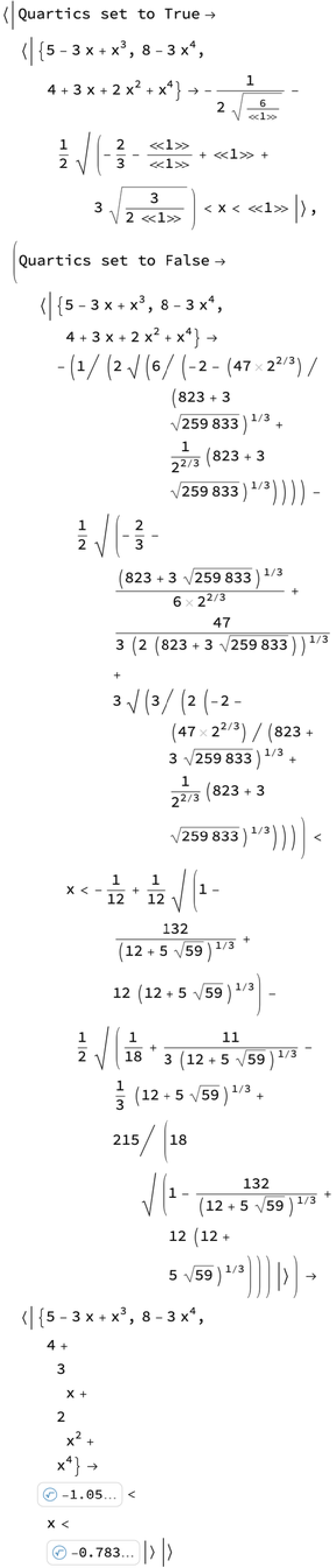
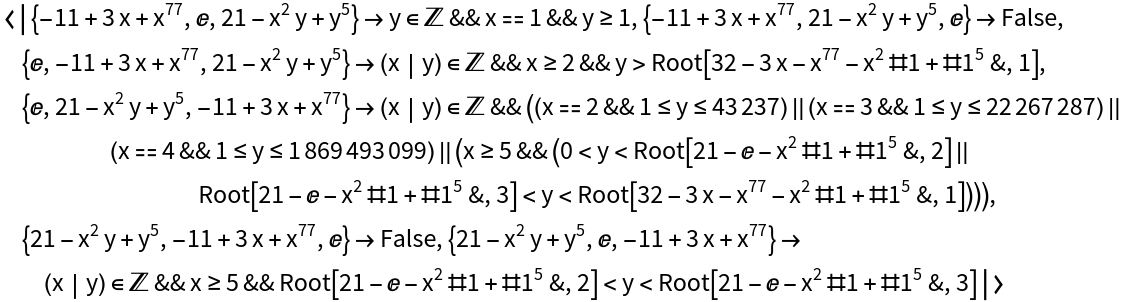
![RegionPlot[
Evaluate[Or @@ Values@ResourceFunction["GenerateOrderingConditions"][Less, explist, {a, b}, "Pattern" -> {a - b, ___}, "AdditionalConstraints" -> a + b < 3]], {a, -3, 3}, {b, -3, 3}, FrameLabel -> {"a", "b"}]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/35b2a3ab6a00484c.png)
![candidate1Region = Module[{votes = {20, 25, 27}, counted = 7/10},
Or @@ Values@
With[{uncounted = Total[votes]/counted - counted}, Quiet@ResourceFunction["GenerateOrderingConditions"][Greater, votes + uncounted*{c1, c2, 1 - (c1 + c2)}, {c1, c2}, "AdditionalConstraints" -> {Total[{c1, c2, 1 - (c1 + c2)}] == 1, 0 <= c1 <= 1, 0 <= c2 <= 1}, "Pattern" -> {1, _, _}, "PatternInterpreter" -> f2, "KeyFunction" -> "Indexed"]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/50f37acc346cc57d.png)
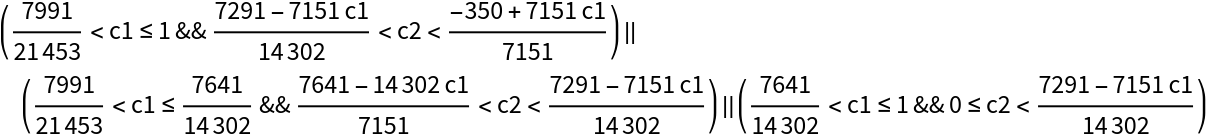
![RegionPlot[candidate1Region, {c1, 0, 1}, {c2, 0, 1}, FrameLabel -> {"fraction of remaining votes for candidate 1", "fraction of remaining votes for candidate 2"}, PlotLabel -> "Path to Victory for Candidate 1"]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/3aa0e29fbb41ec7c.png)

![candidate1Majority = Module[{votes = {20, 25, 27}, counted = 7/10},
Or @@ Values@
With[{uncounted = Total[votes]/counted - counted}, Quiet@ResourceFunction["GenerateOrderingConditions"][Greater, votes + uncounted*{c1, c2, 1 - (c1 + c2)}, {c1, c2}, "AdditionalConstraints" -> {Total[{c1, c2, 1 - (c1 + c2)}] == 1, 0 <= c1 <= 1, 0 <= c2 <= 1, votes[[1]] + uncounted*c1 > 0.5*Total[votes + uncounted*{c1, c2, 1 - (c1 + c2)}]}, "Pattern" -> {1, _, _}, "PatternInterpreter" -> f2, "KeyFunction" -> "Indexed"]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/51cb5e6995c98a26.png)
![RegionPlot[candidate1Majority, {c1, 0, 1}, {c2, 0, 1}, FrameLabel -> {"fraction of remaining votes for candidate 1", "fraction of remaining votes for candidate 2"}, PlotLabel -> "Path to Victory with No Runoff for Candidate 1"]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/57efda16bdec4da3.png)
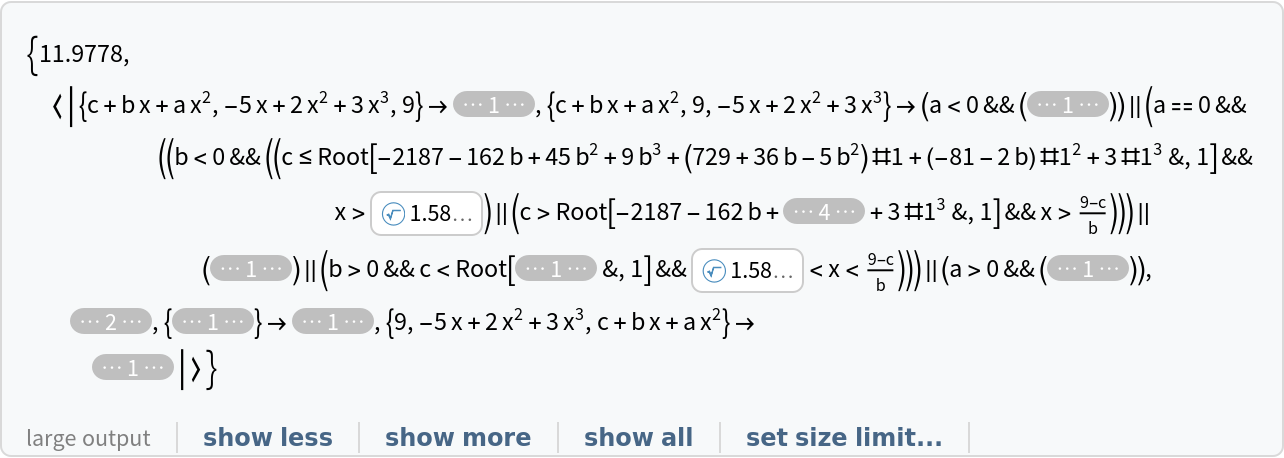
![(votingOrder = ResourceFunction["GenerateOrderingConditions"][GreaterEqual, votes, {x, y}, Reals, "KeyFunction" -> "Indexed"]) // ResourceFunction[
ResourceObject[<|"Name" -> "Terse", "ShortName" -> "Terse", "UUID" -> "6809487c-44ed-4a55-a610-ab706ebb8661", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "An operator form of Short", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/objects/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$369a78f89aa2413eb5b19a962ce89cd7`Terse", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/c1820918-b759-4685-b9b8-c971a81216b5"]|>, ResourceSystemBase -> Automatic]][5]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/032db62ca9bdb3c0.png)
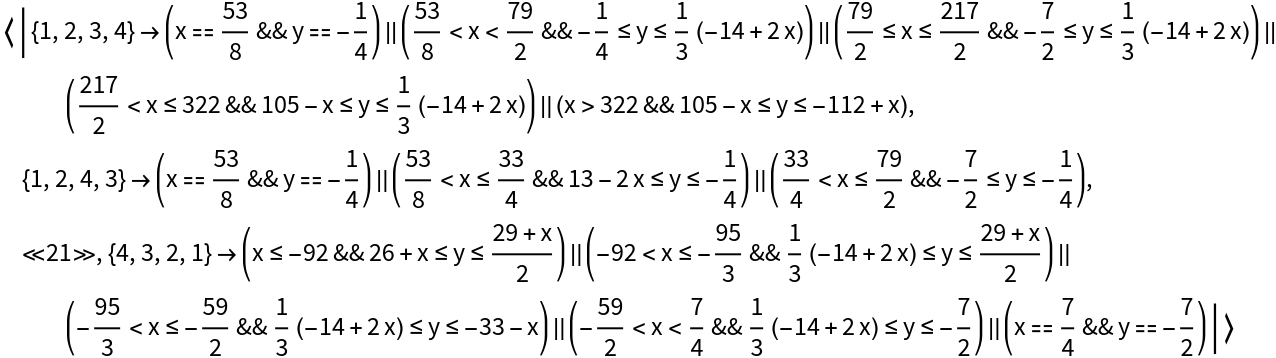
![regions[n_][generatedConditions_] := Query[KeyTake[Range[Length[generatedConditions]]]/*Values, Values/*Apply[Or]][ResourceFunction[
ResourceObject[<|"Name" -> "KeyGroupBy", "ShortName" -> "KeyGroupBy", "UUID" -> "10d8ffd6-2783-4d26-949b-9636792e92ff", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Apply a function to keys of an association and group results by modified keys", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/objects/resourcesystem/api/1.0"],
"SymbolName" -> "FunctionRepository`$9b1c24130d3e49889d3705320461ccb4`KeyGroupBy", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/ef7b080c-c161-4427-8844-33b7cac307c1"]|>, ResourceSystemBase -> Automatic]][
generatedConditions, #[[n]] &]]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/498890661a8ee08a.png)
![Block[{legend},
legend = Legended[#, SwatchLegend[(ColorData[1][#1] &) /@ Range[4], Range[4]]] &; Row@MapThread[{pos, label} |-> With[{plotOperator = (
ResourceFunction[
ResourceObject[<|"Name" -> "MapSlice", "ShortName" -> "MapSlice", "UUID" -> "f3da3843-eca4-49a1-a10f-ae495c5a085e", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Provide the part specifications to a mapped function as a sequence of arguments after the first one", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/objects/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$fc34d7cb86b4477286abcf1aeedb1cac`MapSlice", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/2edb34b0-5ba9-472e-9991-7a8746a6c7a5"]|>, ResourceSystemBase -> Automatic]])[{candidate, index} |-> RegionPlot[candidate, {x, -20, 20}, {y, -20, 20}, PlotLabel -> label, Sequence[
MaxRecursion -> 5, ImageSize -> 350], PlotStyle -> ColorData[1][index]]]},
Apply[Show][plotOperator[regions[pos][votingOrder]]] // legend], {Range[2], {"President", "Vice-President"}}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/7b7081b221809062.png)
![With[{xyDist = MultinormalDistribution[{7, -1}, {{8, 3}, {3, 6}}]}, AssociationMap[
pos |-> With[{reg = regions[pos /. {"President" -> 1, "Vice President" -> 2}][
votingOrder]}, AssociationMap[
candidateIndex |-> NProbability[
reg[[candidateIndex]], {x, y} \[Distributed] xyDist, Method -> "MonteCarlo"], Range[4]]
], {"President", "Vice President"}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/b34/b3488202-1ec3-4cc6-8ea4-8a633725c229/0b2b721f588e9858.png)