Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a hexagonal tiling pattern from a set of hexagonal Wang tiles
ResourceFunction["GenerateHexagonalWangTiling"][tiles, init, n] covers a n-layer hexagonal array with edge-matching Wang tiles, with init as the tile in the center. |
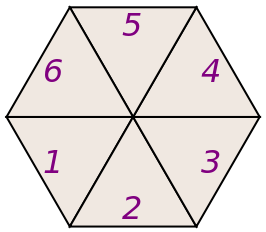 .
.Generate a 1-layer hexagonal tiling with only one Hexagonal Wang tile:
| In[1]:= |
| Out[1]= |  |
Depict the tiling result:
| In[2]:= | ![With[{tiles = {{0, 1, 2, 0, 1, 2}}, size = 2, depictFunction = Function[{tiles, size, result},
Map[With[{pos = Mean[
Catenate[
Part[#, All, 1]]]}, {
MapApply[{
EdgeForm[LightGray],
Opacity[0.9], #2,
Polygon[{pos,
Apply[Sequence, #]}]}& , #], {
EdgeForm[
Directive[Black]],
Opacity[0],
Polygon[
CirclePoints[pos, {2, Pi}, 6]]}}]& ,
MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , {
Map[Partition[
CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& ,
DeleteDuplicates[
Catenate[
NestList[DeleteDuplicates[
Catenate[
Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]},
Graphics[
depictFunction[tiles, size, ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size]], ImageSize -> 200]
]](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7ab0e253-6f90-4f67-a5a7-fa1ff52b022a/50e75968f202d954.png) |
| Out[2]= |  |
Set the tile in the center:
| In[3]:= | ![With[{tiles = {{0, 1, 2, 0, 1, 2}, {2, 0, 1, 2, 0, 1}, {1, 2, 0, 1, 2,
0}}, size = 2, depictFunction = Function[{tiles, size, result},
Map[With[{pos = Mean[
Catenate[
Part[#, All, 1]]]}, {
MapApply[{
EdgeForm[LightGray],
Opacity[0.9], #2,
Polygon[{pos,
Apply[Sequence, #]}]}& , #], {
EdgeForm[
Directive[Black]],
Opacity[0],
Polygon[
CirclePoints[pos, {2, Pi}, 6]]}}]& ,
MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , {
Map[Partition[
CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& ,
DeleteDuplicates[
Catenate[
NestList[DeleteDuplicates[
Catenate[
Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]},
Graphics[
depictFunction[tiles, size, ResourceFunction["GenerateHexagonalWangTiling"][
tiles, {1, 2, 0, 1, 2, 0}, size]], ImageSize -> 200]
]](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7ab0e253-6f90-4f67-a5a7-fa1ff52b022a/23818aa742fa8e75.png) |
| Out[3]= | 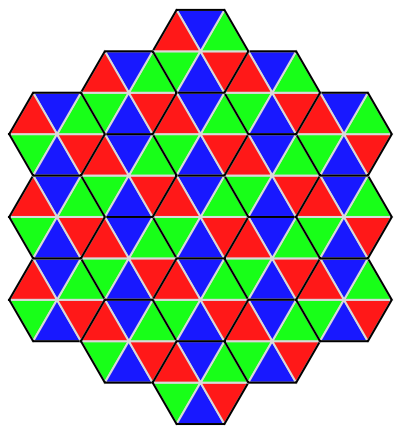 |
Make a bigger patch with 4-layer surroundings:
| In[4]:= | ![With[{tiles = {{1, 0, 1, 1, 0, 1}}, size = 4, depictFunction = Function[{tiles, size, result},
Map[With[{pos = Mean[
Catenate[
Part[#, All, 1]]]}, {
MapApply[{
EdgeForm[LightGray],
Opacity[0.9], #2,
Polygon[{pos,
Apply[Sequence, #]}]}& , #], {
EdgeForm[
Directive[Black]],
Opacity[0],
Polygon[
CirclePoints[pos, {2, Pi}, 6]]}}]& ,
MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , {
Map[Partition[
CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& ,
DeleteDuplicates[
Catenate[
NestList[DeleteDuplicates[
Catenate[
Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]},
Graphics[
depictFunction[tiles, size, ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size]], ImageSize -> 200]
]](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7ab0e253-6f90-4f67-a5a7-fa1ff52b022a/05d577a3554f5564.png) |
| Out[4]= |  |
Generate aperiodic hexagonal Wang tiling:
| In[5]:= | ![With[{tiles = CompressedData["
1:eJw1j8ENAzEIBDEYG2xTRPpIFSnhGkj/v8Be7mGNLI3Y3df1/VxMRO98Ix81
ll5Q6fmfKgYw0Nj67bhJOb4EDsC2DI4b0fbZ0tlrtil0HnibRmd7a0ZhxOkA
U0KIFSCdFmKkzcIza4/umbVP98o6fVXWGauy9lh5oPoAqw5Un7qTfepO9olQ
dA5F52B0TlRn4O/kvHJyOxyAH3SK3F6dc3t1rtH6ANu1dimcvINdDOcGsmrX
D9SMCUo=
"], size = 10, depictFunction = Function[{tiles, size, result},
Map[With[{pos = Mean[
Catenate[
Part[#, All, 1]]]}, {
MapApply[{
EdgeForm[LightGray],
Opacity[0.9], #2,
Polygon[{pos,
Apply[Sequence, #]}]}& , #], {
EdgeForm[
Directive[Black]],
Opacity[0],
Polygon[
CirclePoints[pos, {2, Pi}, 6]]}}]& ,
MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , {
Map[Partition[
CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& ,
DeleteDuplicates[
Catenate[
NestList[DeleteDuplicates[
Catenate[
Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]},
With[{tiling = ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size]},
Labeled[
Graphics[depictFunction[tiles, size, tiling, ImageSize -> 800]]
, Grid[
Partition[
Graphics[{#, {EdgeForm[Black], Opacity[0], Polygon[CirclePoints[{0, 0}, {2, \[Pi]}, 6]]}}, ImageSize -> 20] &@
MapThread[{Hue[#2], EdgeForm[LightGray], Polygon[{{0, 0}, Sequence @@ #1}]} &,
{Partition[CirclePoints[{0, 0}, {2, \[Pi]}, 6], 2, 1, 1], #/(Max[tiles] + 1)}] & /@ tiles
, 10]]]
]]](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7ab0e253-6f90-4f67-a5a7-fa1ff52b022a/6b1bbbccc331a37a.png) |
| Out[5]= | 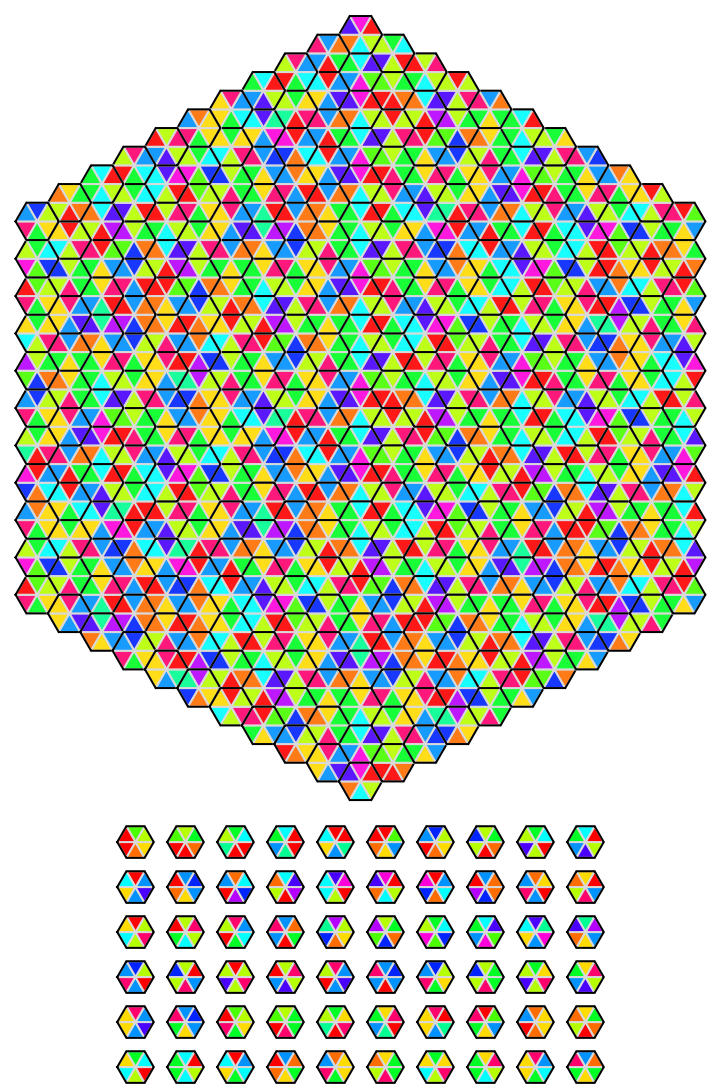 |
Give two different possible tilings using "Count":
| In[6]:= | ![With[{tiles = {{1, 2, 0, 1, 2, 0}, {2, 0, 1, 2, 0, 1}, {0, 1, 2, 0, 1,
2}, {1, 2, 0, 1, 2, 0}, {2, 0, 1, 2, 0, 1}, {0, 1, 2, 0, 1, 2}}, size = 3, depictFunction = Function[{tiles, size, result},
Map[With[{pos = Mean[
Catenate[
Part[#, All, 1]]]}, {
MapApply[{
EdgeForm[LightGray],
Opacity[0.9], #2,
Polygon[{pos,
Apply[Sequence, #]}]}& , #], {
EdgeForm[
Directive[Black]],
Opacity[0],
Polygon[
CirclePoints[pos, {2, Pi}, 6]]}}]& ,
MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , {
Map[Partition[
CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& ,
DeleteDuplicates[
Catenate[
NestList[DeleteDuplicates[
Catenate[
Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]},
Graphics[depictFunction[tiles, size, #, ImageSize -> 200]] & /@ ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size, "Count" -> 2]
] // List // Grid[#, Frame -> All, FrameStyle -> LightGray] &](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7ab0e253-6f90-4f67-a5a7-fa1ff52b022a/44758085c0f6254e.png) |
| Out[6]= |  |
Give all possible tilings:
| In[7]:= | ![With[{tiles = {{1, 2, 0, 1, 2, 0}, {2, 0, 1, 2, 0, 1}, {0, 1, 2, 0, 1,
2}, {1, 2, 0, 1, 2, 0}, {2, 0, 1, 2, 0, 1}, {0, 1, 2, 0, 1, 2}}, size = 3, depictFunction = Function[{tiles, size, result},
Map[With[{pos = Mean[
Catenate[
Part[#, All, 1]]]}, {
MapApply[{
EdgeForm[LightGray],
Opacity[0.9], #2,
Polygon[{pos,
Apply[Sequence, #]}]}& , #], {
EdgeForm[
Directive[Black]],
Opacity[0],
Polygon[
CirclePoints[pos, {2, Pi}, 6]]}}]& ,
MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , {
Map[Partition[
CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& ,
DeleteDuplicates[
Catenate[
NestList[DeleteDuplicates[
Catenate[
Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]},
Graphics[depictFunction[tiles, size, #, ImageSize -> 200]] & /@ ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size, "Count" -> All]
] // List // Grid[#, Frame -> All, FrameStyle -> LightGray] &](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7ab0e253-6f90-4f67-a5a7-fa1ff52b022a/46fe75a3ceafa9a4.png) |
| Out[7]= | 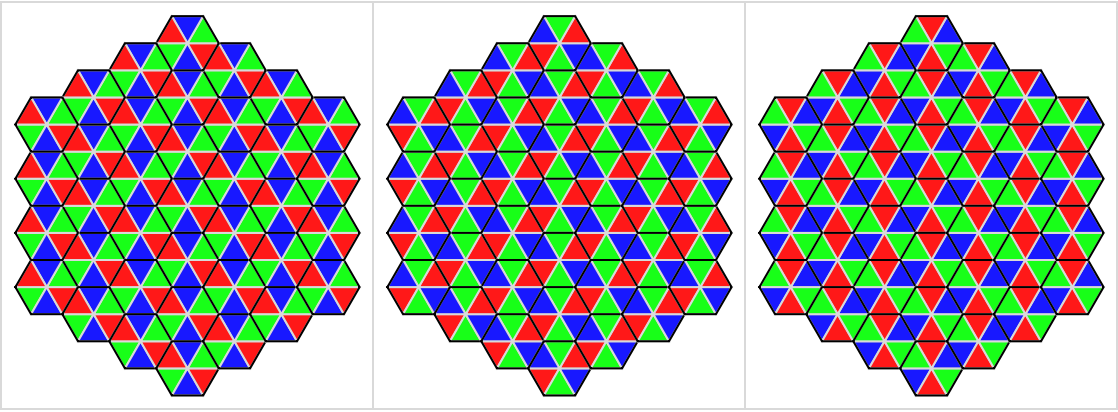 |
The number order in the 3-layer grid of the tiles is shown as following:
| In[8]:= | ![With[{centerPoints = DeleteDuplicates[Catenate[
NestList[
DeleteDuplicates@
Catenate[
CirclePoints[#, {2 Sqrt[3], 7 Pi/6}, 6] & /@ #] &, {{0, 0}}, 3]
]]},
Graphics[
MapIndexed[{Opacity[1], EdgeForm[Black], White, Polygon[CirclePoints[#1, {2, Pi}, 6]], Black, Text[First[#2], #1]} &, centerPoints]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7ab0e253-6f90-4f67-a5a7-fa1ff52b022a/16fae4527d8b784d.png) |
| Out[8]= | 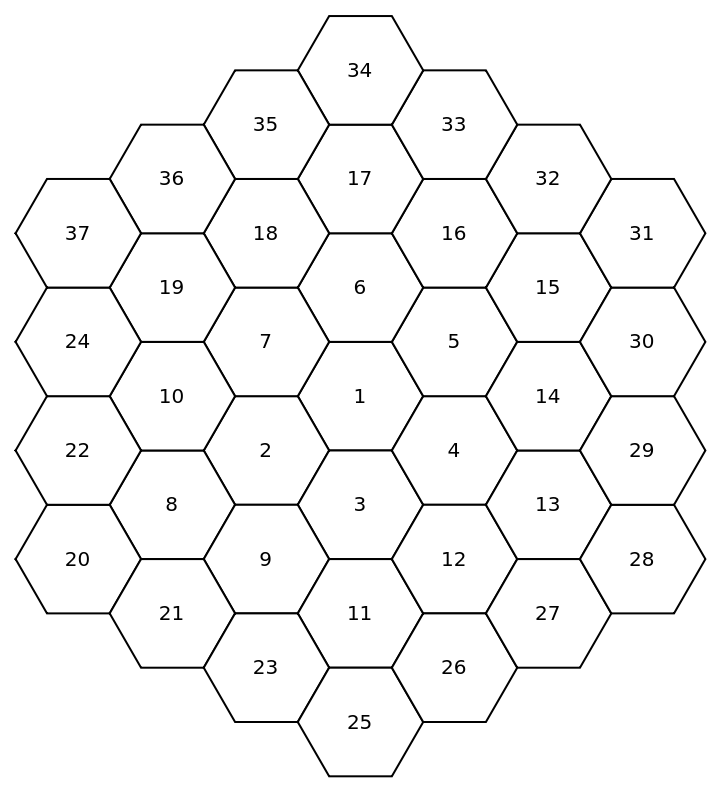 |
Generate tilings of three different sets of aperiodic Hexagonal Wang tiles, all derived from the Hat tile:
| In[9]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/4c7093e6-3139-426d-ac10-b6f0c5d7c11f"]](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7ab0e253-6f90-4f67-a5a7-fa1ff52b022a/69ff186d7cb87f40.png) |
| Out[9]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License