Basic Examples (4)
Define a cissoid:
Plot it:
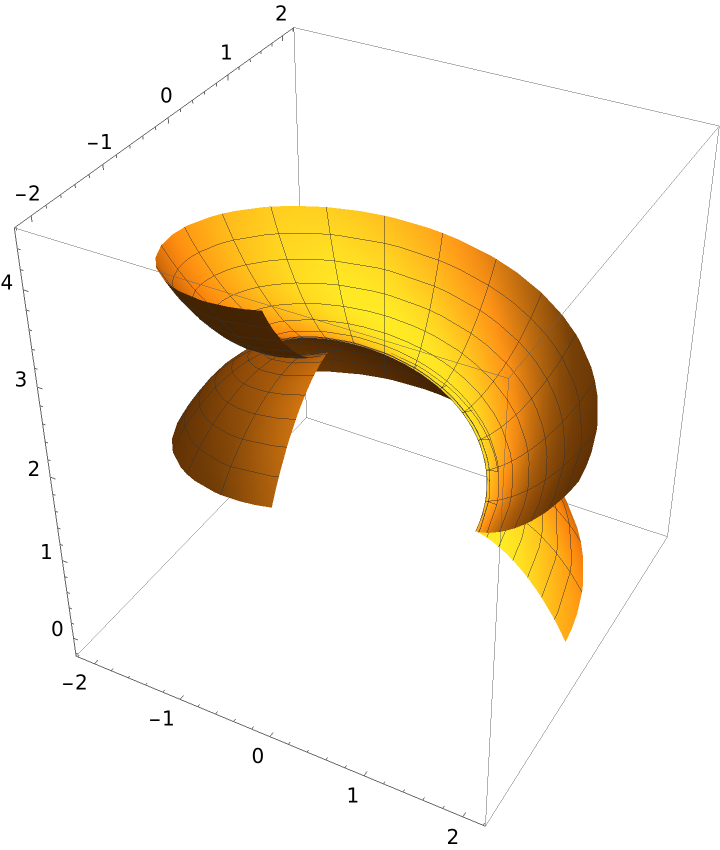
The generalized helicoid of a cissoid:
Plot the resulting surface:
Scope (2)
The generalized helicoid of a sinusoidal curve:
Plot the resulting surface:
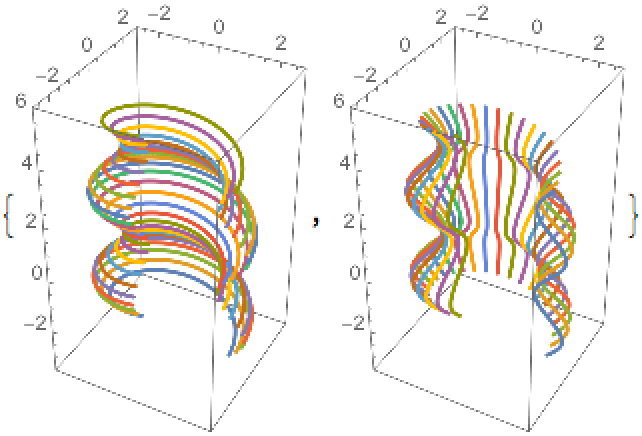
Plot parallel helical curves and meridians:
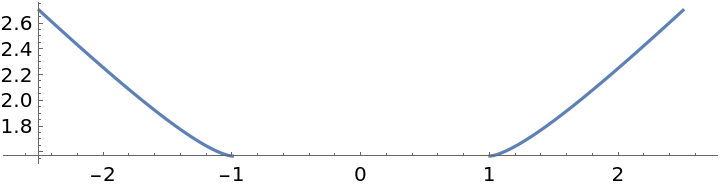
A surface is a flat generalized helicoid if its profile curve can be parametrized as α(t)=(t,ψ(t)), where 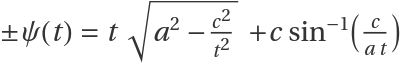 :
:
A flat generalized helicoid (for simplicity we set a=c=1):
Being flat means having zero Gaussian curvature. The Gaussian curvature of a surface can be computed via the resource function GaussianCurvature:
Plot the zero-curvature profile curves:
Plot the flat generalized helicoid for these curves:
Properties and Relations (2)
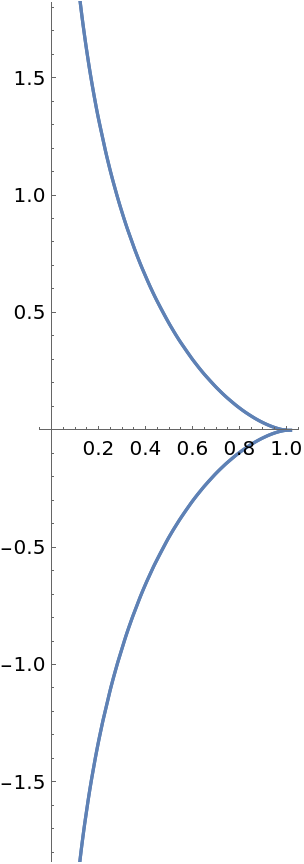
Define a tractrix:
Plot it:
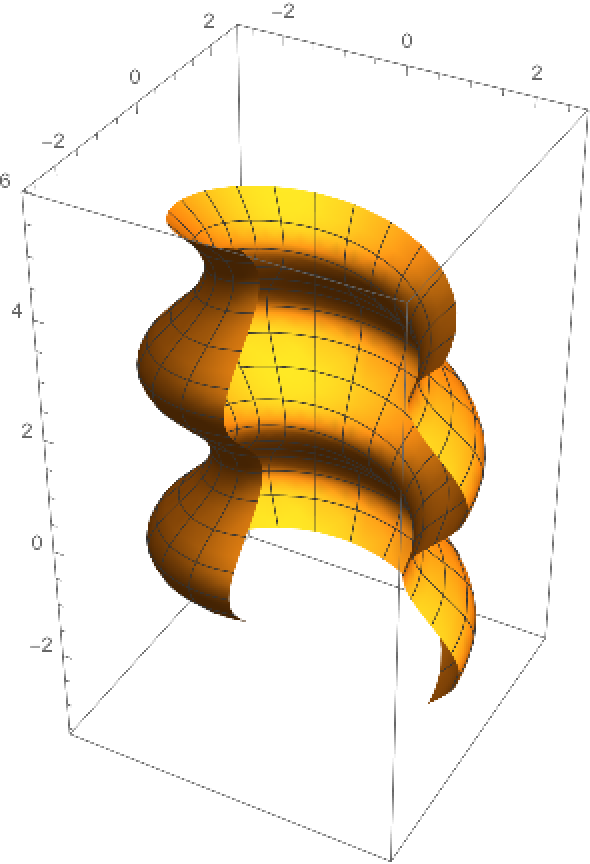
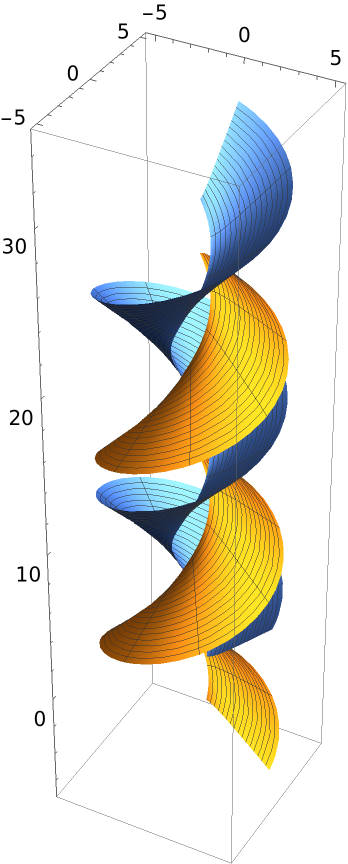
Compute the generalized helicoid of a tractrix:
Plot the generalized helicoid:
The generalized helicoid of a tractrix is a surface of Dini:
Here is some code to create a curve with prescribed (intrinsic) curvature:
Define a curve with linear intrinsic curvature:
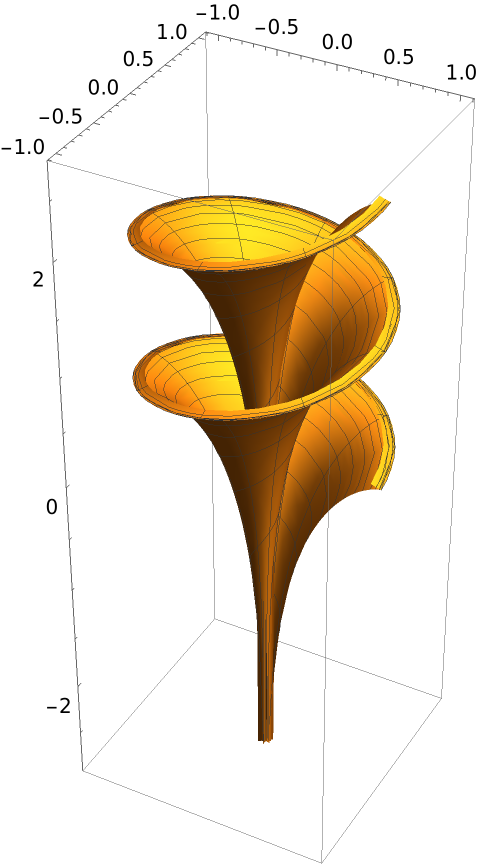
The generalized helicoid for the previous curvature:
Plot the profile curve:
Plot the generalized helicoid surface for a linear intrinsic curvature (profile curve in red):
Properties and Relations (7)
A generalized helix of a circle:
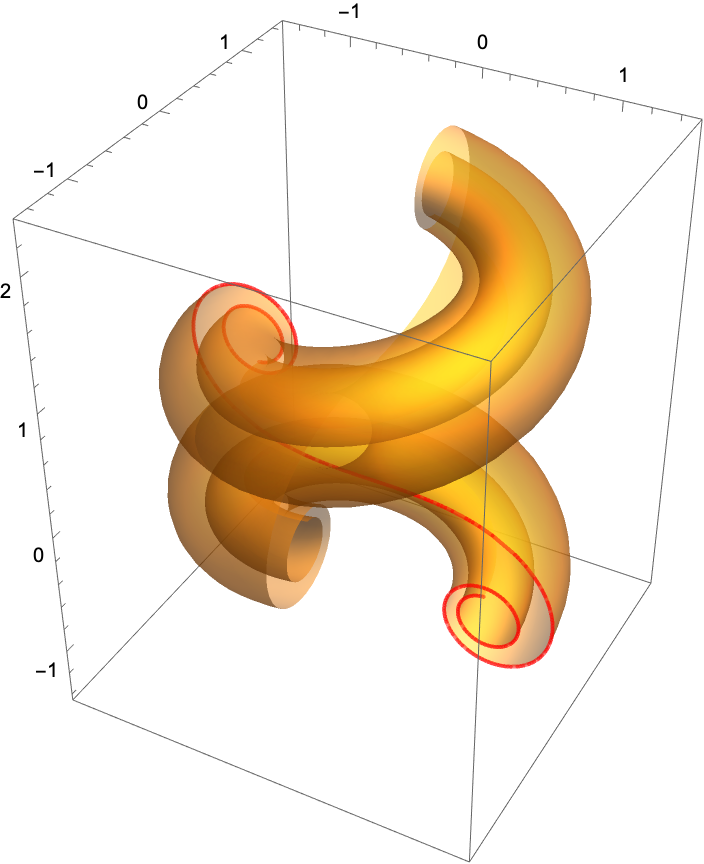
A twisphere has a parametrization of a generalized helix type:
Plot the twisphere:
Compute the Gaussian curvature with the resource function GaussianCurvature:
Compute mean curvature with the resource function MeanCurvature:
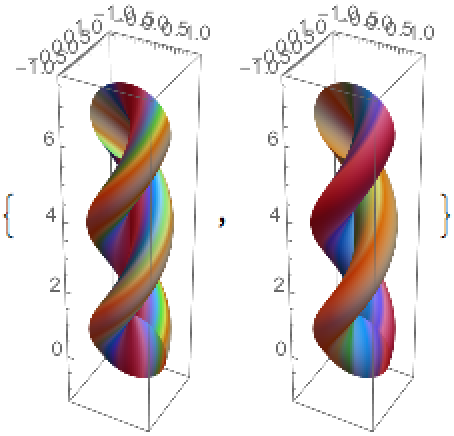
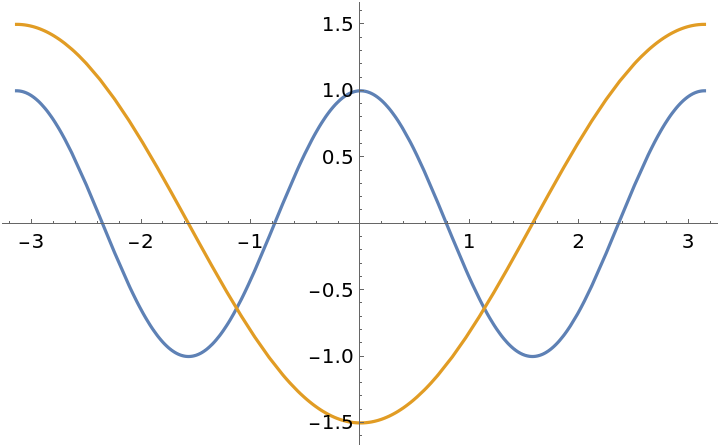
Plot both curvatures:
Plot the twisphere according to both curvatures:

![]() :
:![ResourceFunction["GaussianCurvature"][
ResourceFunction["GeneralizedHelicoid"][zcprofile[#, 1, 1][t], 1, {u, v}], {u, t}] & /@ {-1, 1}](https://www.wolframcloud.com/obj/resourcesystem/images/c02/c02813fc-650a-487a-8440-770ef3bbb5db/37757c95cb3e2292.png)
![Show[ParametricPlot3D[
ResourceFunction["GeneralizedHelicoid"][zcprofile[#, 1, 1][v], 2, u] & /@ {-1, 1} // Evaluate, {u, 0, 9 \[Pi]/2}, {v, 1, 5}, PlotPoints -> {40, 10}]]](https://www.wolframcloud.com/obj/resourcesystem/images/c02/c02813fc-650a-487a-8440-770ef3bbb5db/3b0b3a2fb6a3b323.png)
![intrinsic[f_, a_, {c_, d_, e_}, {min_, max_}][t_] :=
Module[{x, y, \[Theta], s},
eqic = {x'[s] == Cos[\[Theta][s]], y'[s] == Sin[\[Theta][s]], \[Theta]'[s] == f[s], x[a] == c, y[a] == d, \[Theta][a] == e};
sol = NDSolve[eqic, {x, y, \[Theta]}, {s, min, max}];
{x[t], y[t]} /. sol[[1]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/c02/c02813fc-650a-487a-8440-770ef3bbb5db/5b9381cd75247233.png)

![ParametricPlot3D[
Evaluate[ResourceFunction["GeneralizedHelicoid"][f[v], 0.2, u]] /. u -> .5, {v, -5, 5}, Mesh -> False, PlotStyle -> Opacity[.5], MaxRecursion -> 3]](https://www.wolframcloud.com/obj/resourcesystem/images/c02/c02813fc-650a-487a-8440-770ef3bbb5db/7986c4a983e06e08.png)

![Show[ParametricPlot3D[
Evaluate[
ResourceFunction["GeneralizedHelicoid"][f[v], 0.2, u]], {u, 0, 3 \[Pi]/2}, {v, -5, 5}, PlotPoints -> {30, 60}, Mesh -> False, PlotStyle -> Opacity[.5], MaxRecursion -> 3], ParametricPlot3D[
Evaluate[ResourceFunction["GeneralizedHelicoid"][f[v], 0.2, u]] /. u -> 0, {v, -5, 5}, Mesh -> False, PlotStyle -> {Opacity[.5], Red},
MaxRecursion -> 3]]](https://www.wolframcloud.com/obj/resourcesystem/images/c02/c02813fc-650a-487a-8440-770ef3bbb5db/38f0d1cfea953cba.png)

![ParametricPlot3D[
Evaluate[twisphere[1, 1][u, v]], {u, 0, 2 \[Pi]}, {v, -\[Pi], \[Pi]}, Lighting -> True, PlotPoints -> {40, 40}, Mesh -> False, MeshFunctions -> Function[{x, y, z, u, v}, #], ColorFunction -> Function[{x, y, z, u, v}, ColorData["BrightBands"][#]], ColorFunctionScaling -> False, ImageSize -> Small] & /@ {Rescale[
gcur, {-1, 1}], Rescale[mcur, {-1.5, 1.5}]}](https://www.wolframcloud.com/obj/resourcesystem/images/c02/c02813fc-650a-487a-8440-770ef3bbb5db/53acf04b148578fb.png)