Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Create fractals with random partial jumps toward reference points
ResourceFunction["GeneralizedChaosGame"][reg,n] plots a fractal by iteratively jumping n times toward a random point inside the reference geometry reg by jumping halfway. | |
ResourceFunction["GeneralizedChaosGame"][reg,n,jspec] uses the jumping specification jspec. | |
ResourceFunction["GeneralizedChaosGame"][reg,n,jspec,format] formats the result according to the output specification format. |
| n | n points equally spaced around the unit circle |
| {p1,p2,…} | uses the points pi as the reference geometry |
| reg | uses the region reg as the reference geometry |
| n | performs n iterations |
| Automatic | performs 104 iterations |
| α | jumps a distance α toward the next reference point |
| Scaled[α] | jumps a fraction α toward the next reference point |
| Automatic | jumps halfway toward the next reference point |
| {s1,s2,…} | cycle through the jumping specifications si |
| {"OriginIndexed", {s1,s2,…sn}} | jump using jump specification si, where i is the index of the last visited reference point |
| {“DestinationIndexed”, {s1,s2,…sn}} | jump using jump specification si, where i is the index of the next reference point |
| func | uses the function func to calculate the next position |
| "Graphics" | outputs a graphical representation of the results |
| "List" | outputs the list of coordinates visited |
| "DensityPlot" | outputs a graphical representation of the density of points |
| "PointStyle" | Automatic | style to use for the points |
| "ReferenceGeometryStyle" | Automatic | style to use for the reference geometry |
| "Probabilities" | Automatic | list of probabilities representing the chance to jump to each reference point |
| "ExclusionRegionFunction" | None | jumps that land on positions for which the function yields True are not allowed |
| "Choices" | All | restrict the possible points to jump to based on the current position or history |
| "ColorFunction" | Automatic | will use the color function ColorFunction as defined in ArrayPlot |
| "BinningSpecification" | Automatic | a list of binning specifications to use for the output format |
| "Absolute"→{b1,b2,…,bn} | restrict the jump to the reference points pi for which bi are True |
| "Relative"→{b1,b2,…,bn} | restrict the jump to the reference points pi (counted relative to the last position) for which bi are True |
| {{xmin,xmin,dx}, {ymin,ymax,dy}} | bins using the x specification and y specification |
| {dx,dy} | bins the data in bins of size dx by dy |
Create the classic Sierpiński triangle using 30,000 iterations:
| In[1]:= |
| Out[1]= |  |
Jump only 40% of the way toward the reference points:
| In[2]:= |
| Out[2]= |  |
Jump between 4 corners of a trapezoid:
| In[3]:= |
| Out[3]= |  |
Jump between random points on a circle:
| In[4]:= |
| Out[4]= | 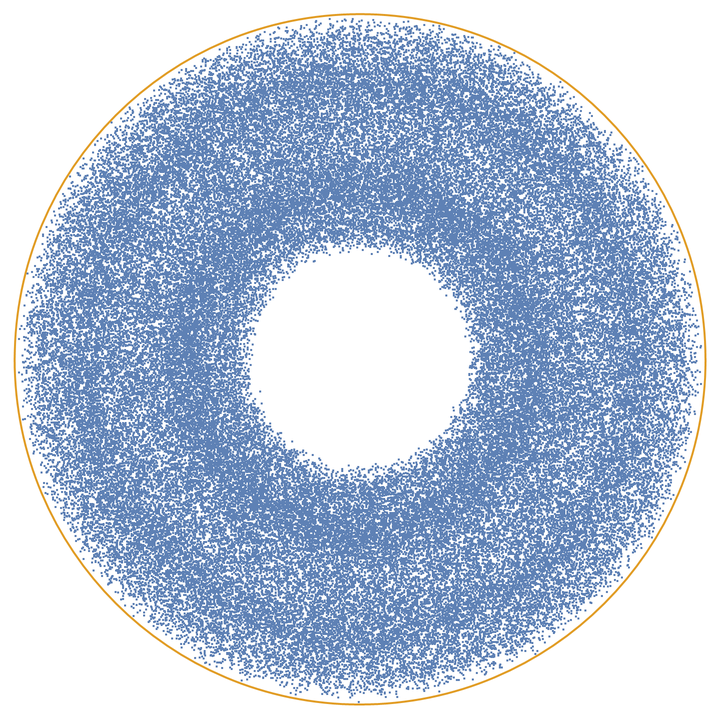 |
Give the geometry as a list of points:
| In[5]:= |
| Out[5]= |  |
The reference geometry can be any region, e.g. a Line:
| In[6]:= |
| Out[6]= |  |
Perform the chaos game in higher dimensions:
| In[7]:= | ![tetrahedronpoints = {{0., 0., 0.6123724356957945}, {-0.2886751345948129, -0.5, -0.20412414523193154`}, {-0.2886751345948129, 0.5, -0.20412414523193154`}, {0.5773502691896258, 0., -0.20412414523193154`}};
ResourceFunction["GeneralizedChaosGame"][tetrahedronpoints]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/3156f5c6beaeadd8.png) |
| Out[8]= |  |
Combine different regions using RegionUnion:
| In[9]:= |
| Out[9]= |  |
The default jump specification is Scaled[0.5]:
| In[10]:= |
| Out[10]= |  |
| In[11]:= |
| Out[11]= |  |
Perform the chaos game using a 40% jump:
| In[12]:= |
| Out[12]= |  |
Perform the chaos game using a jump with a distance of 0.7:
| In[13]:= |
| Out[13]= |  |
Alternate between a fractional and a distance jump to create a blurry Sierpiński triangle:
| In[14]:= |
| Out[14]= |  |
Alternating between a fractional and a distance jump creates a different result compared to the individual specifications:
| In[15]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/5c58ad39-28e8-4302-b19d-0d1f301c05a2"]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/18124844f05c12ff.png) |
| Out[15]= |  |
Jump 50%, 60% or 40% if the last reference point was point 1, 2 or 3, respectively:
| In[16]:= |
| Out[16]= |  |
Jump 50%, 60% or 40% if the next reference point is point 1, 2 or 3, respectively:
| In[17]:= |
| Out[17]= |  |
Jump a distance of 1.75 toward the top point, and 0.5 toward all other points:
| In[18]:= |
| Out[18]= |  |
Use a pure function to get a combination of fractional and distance jumping:
| In[19]:= |
| Out[19]= | 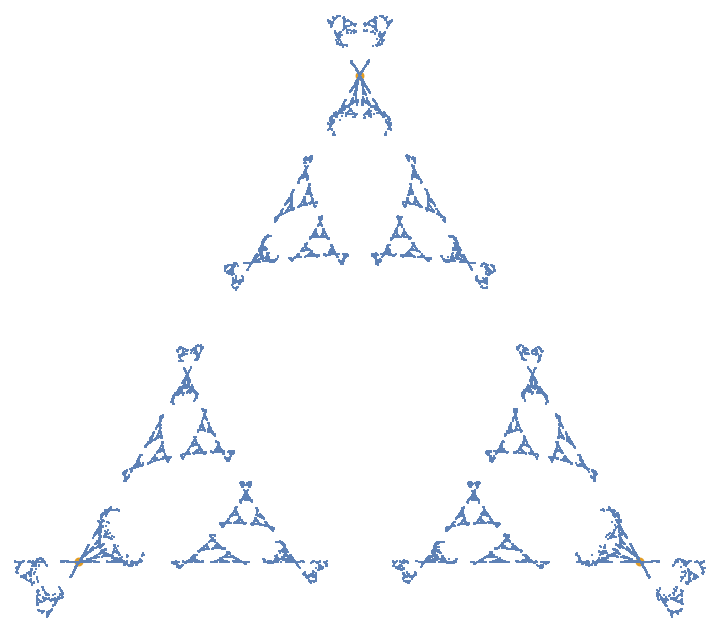 |
Use more complicated functions:
| In[20]:= |
| Out[20]= |  |
| In[21]:= |
| Out[21]= |  |
The default is a graphical output:
| In[22]:= |
| Out[22]= |  |
Obtain the results as a list and perform an operation on it:
| In[23]:= |
| Out[24]= |  |
Output a density plot instead:
| In[25]:= |
| Out[25]= | 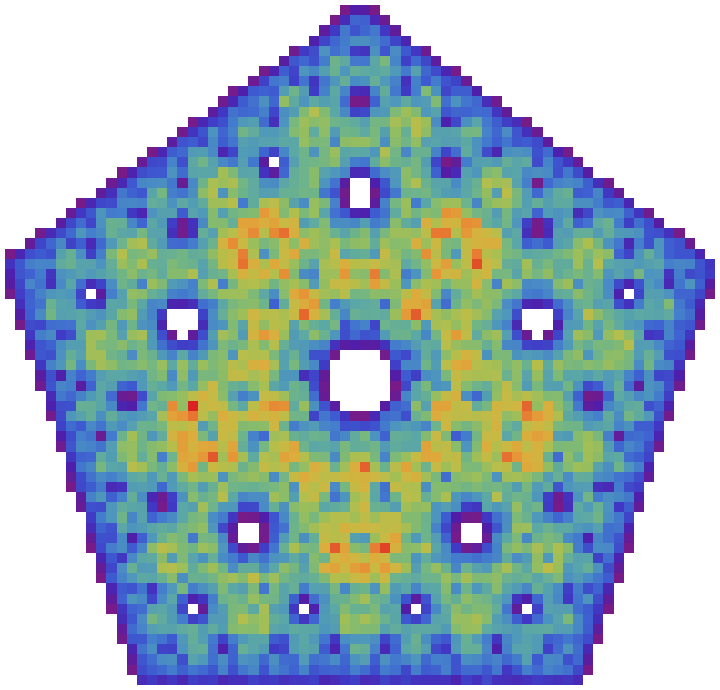 |
Change the style of the points:
| In[26]:= |
| Out[26]= |  |
Change the style of the reference geometry:
| In[27]:= |
| Out[27]= |  |
| In[28]:= |
| Out[28]= | 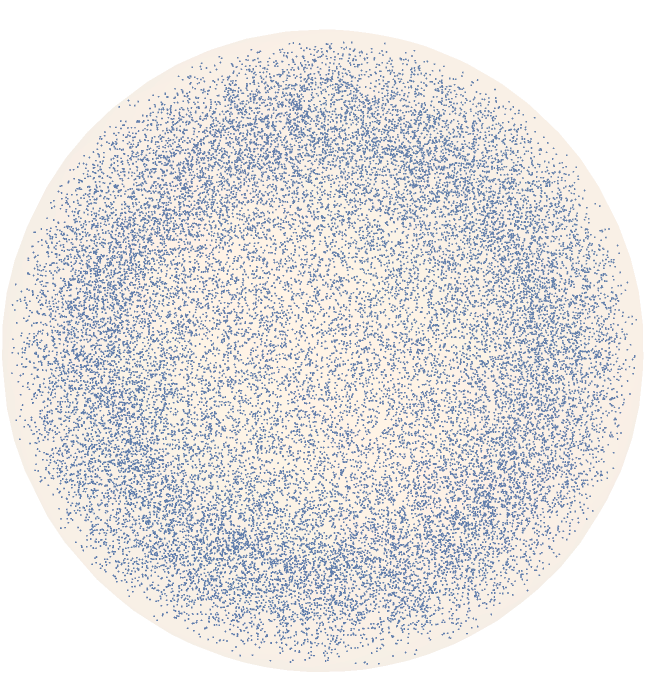 |
Change the probability to jump to each reference point:
| In[29]:= |
| Out[29]= | 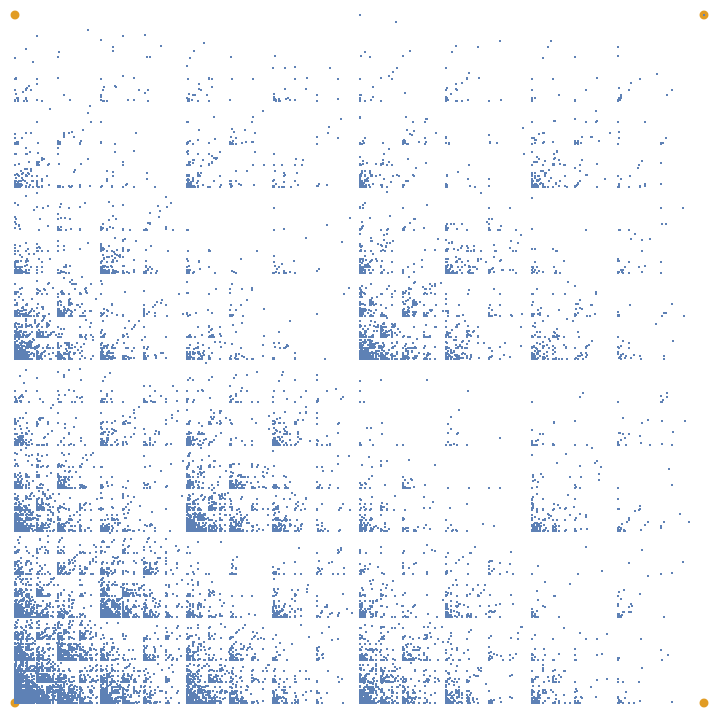 |
Restrict certain landing locations:
| In[30]:= |
| Out[30]= | 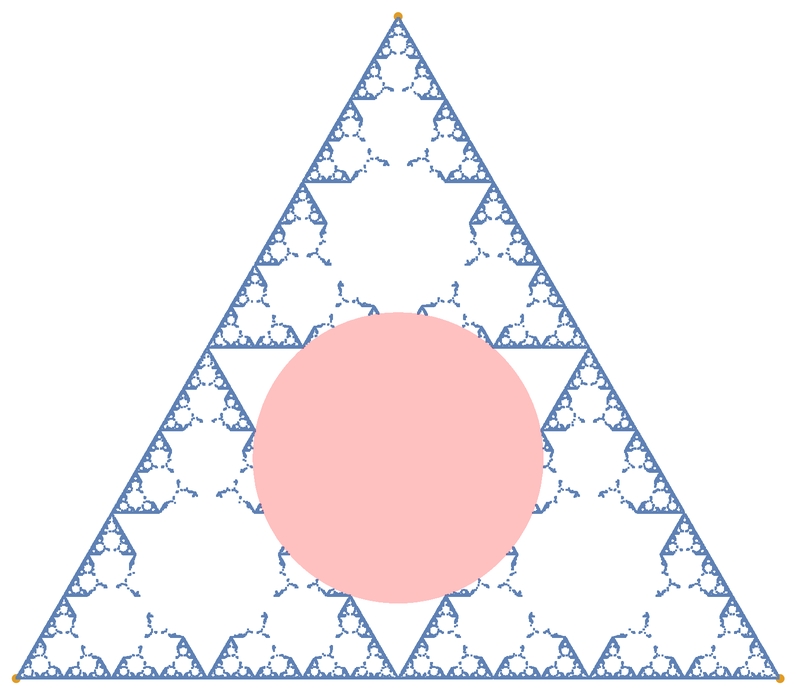 |
Restrict the point to fall in a circle at the top:
| In[31]:= | ![ResourceFunction["GeneralizedChaosGame"][4, 100000, Scaled[0.5], "ExclusionRegionFunction" -> Function[{x, y}, x^2 + (y - Sqrt[1/2])^2 < 0.5]]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/7ca7e2e372bc3d56.png) |
| Out[31]= | 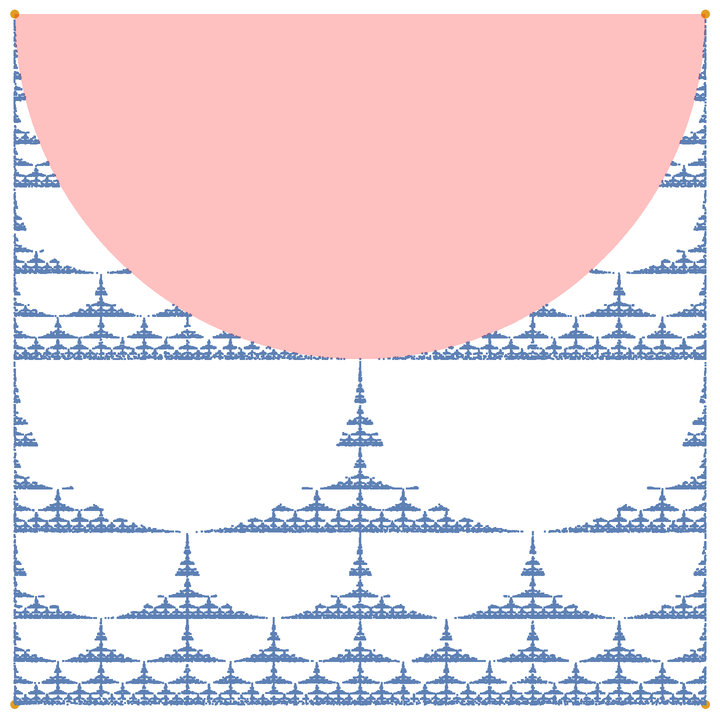 |
Allow a jump of only 1, 3 or 4 reference points ahead as compared to the last reference point:
| In[32]:= |
| Out[32]= |  |
Allow a jump only to points 2, 3 or 4:
| In[33]:= |
| Out[33]= |  |
Jump possibilities can be made to depend on history. Do not allow to jump 1 ahead from the last reference point and 3 ahead from the penultimate reference point:
| In[34]:= | ![ResourceFunction["GeneralizedChaosGame"][4, 10^4, "Choices" -> "Relative" -> {{True, False, False, True}, {True, True, False, True}, {True, True, False, False}, {False, True, False, True}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/1d72b5128dd2d772.png) |
| Out[34]= |  |
Have the jump choices depend on the previously visited point:
| In[35]:= | ![ResourceFunction[
"GeneralizedChaosGame"][{{-1, -1}, {1, -1}, {1, 1}, {-1, 1}}, 3 10^4,
Scaled[0.5], "Choices" -> "Absolute" -> {{False, True, True, False}, {True, False, False, True}, {True, True, True, True}, {True, True, True, True}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/2903155b3801bc0a.png) |
| Out[35]= |  |
For a density plot, specify the color function used:
| In[36]:= |
| Out[36]= | 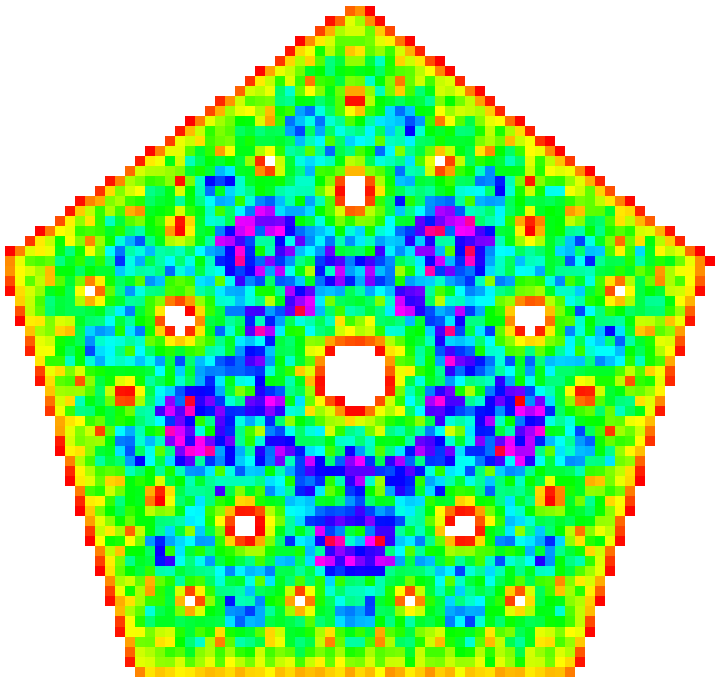 |
The default is the rainbow color function:
| In[37]:= |
| Out[37]= | 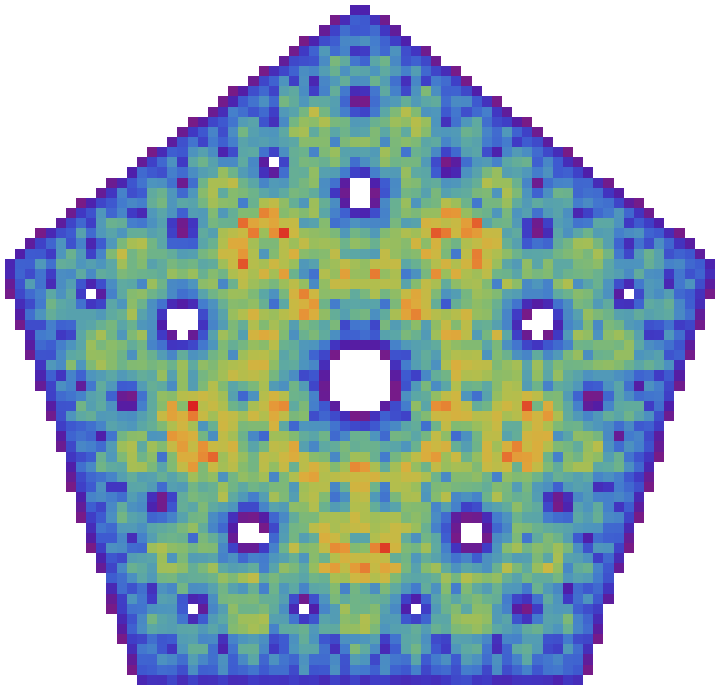 |
For a density plot, specify the binning specification:
| In[38]:= |
| Out[38]= | 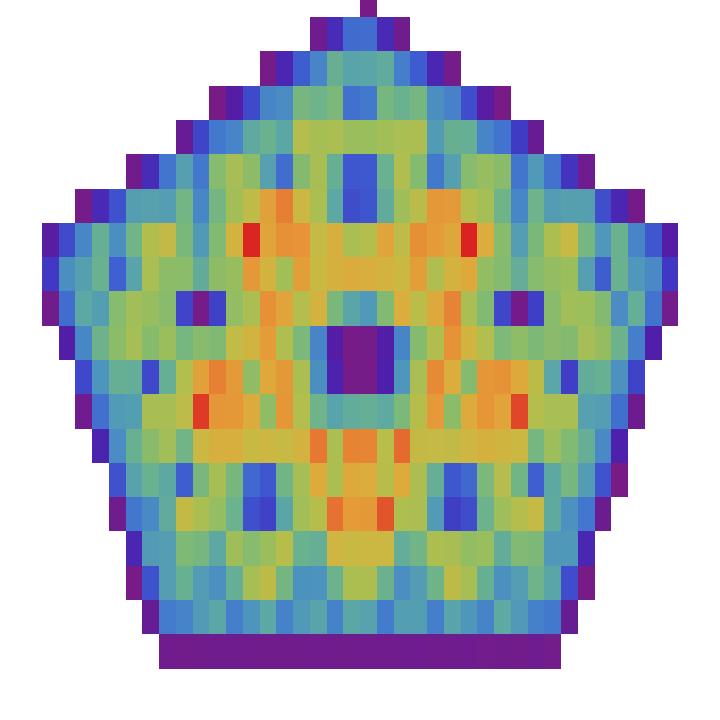 |
Or specify just the size of the bins:
| In[39]:= |
| Out[39]= | 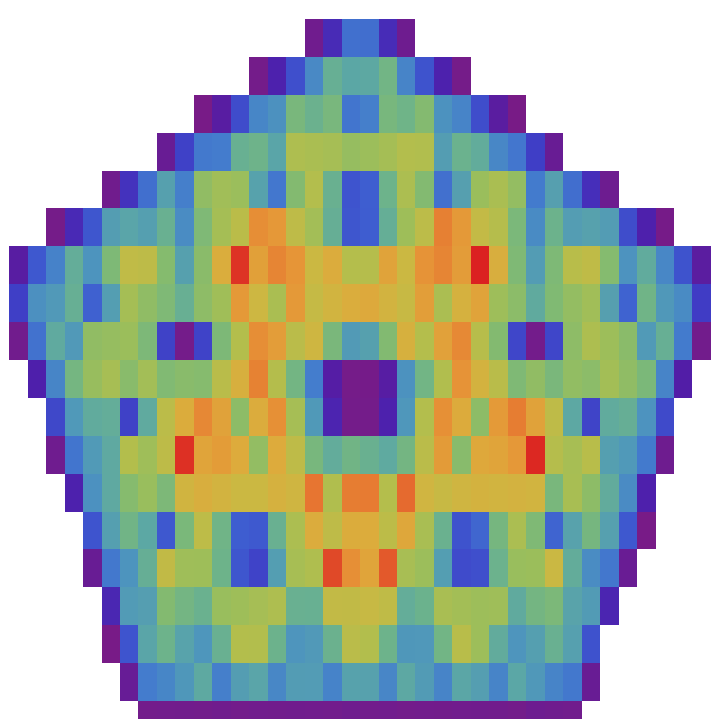 |
Explore jumping in different dimensions. Calculate the jumping in (hyper)spheres in 2D–8D, and then plot the histogram of the distance from the center:
| In[40]:= | ![dims = Range[2, 8]
pts = ResourceFunction["GeneralizedChaosGame"][
Sphere[ConstantArray[0, #]], 5 10^4, Scaled[0.7], "List"] & /@ dims;](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/361be530d4a8f97c.png) |
| Out[40]= |
| In[41]:= | ![bspec = {0, 1, 0.025};
bins = MovingAverage[Range @@ bspec, 2];
bc = BinCounts[Norm /@ #, bspec] & /@ pts;
ListPlot[Transpose[{bins, #}] & /@ bc, Joined -> True, PlotLegends -> dims, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/2a2fcf50c17f2d27.png) |
| Out[44]= | 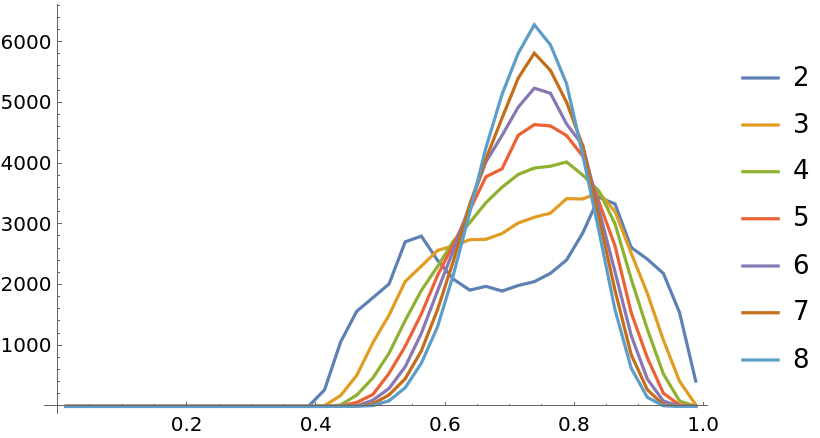 |
Produce the Sierpiński triangle as in a rule 90 cellular automaton:
| In[45]:= |
| Out[45]= | 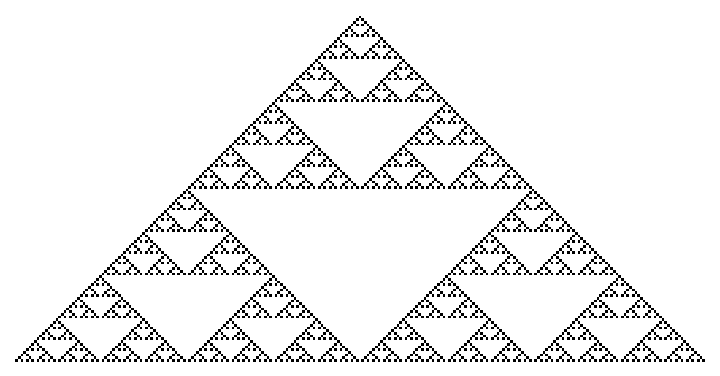 |
| In[46]:= |
| Out[46]= |  |
The reference geometry might occlude all the points:
| In[47]:= |
| Out[47]= |  |
Use the option "ReferenceGeometryStyle" to make the points visible:
| In[48]:= |
| Out[48]= |  |
For a one-dimensional chaos game, explicit braces are needed:
| In[49]:= |
| Out[49]= |
| In[50]:= |
| Out[50]= |  |
For each possible choice, there should be at least one True element:
| In[51]:= | ![ResourceFunction["GeneralizedChaosGame"][4, "Choices" -> "Absolute" -> {{True, False, True, True}, {True, False, True, True}, {False, False, False, False}, {True, True, False, True}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/4075127a8afa930d.png) |
| Out[51]= |
The "Choices" option can only be used when the region is a discrete set of points:
| In[52]:= | ![ResourceFunction["GeneralizedChaosGame"][Circle[{0, 0}], "Choices" -> "Absolute" -> {{True, False, True, True}, {True, False, True, True}, {False, False, False, False}, {True, True, False, True}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/6e4a86688b446438.png) |
| Out[52]= |
The "Probabilities" option can only be used when the region is a discrete set of points:
| In[53]:= |
| Out[53]= |
Recreate the Barnsley fern:
| In[54]:= | ![a1 = {{0, 0}, {0, 0.16}};
a2 = {{0.85, 0.04}, {-0.04, 0.85}};
a3 = {{0.2, -0.26}, {0.23, 0.22}};
a4 = {{-0.15, 0.28}, {0.26, 0.24}};
o2 = {0, 1.6};
o3 = {0, 1.6};
o4 = {0, 0.44};
l = ResourceFunction["GeneralizedChaosGame"][ConstantArray[0, {4, 2}],
10^5, {"DestinationIndexed", {a1 . #1 &, a2 . #1 + o2 &, a3 . #1 + o3 &, a4 . #1 + o4 &}}, "Probabilities" -> {1, 85, 7, 7}]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/0008b4f2c08feb95.png) |
| Out[61]= |  |
Jump halfway and then jump a distance of 0.2 in the perpendicular direction:
| In[62]:= | ![Show[ResourceFunction["GeneralizedChaosGame"][2, 10^5, 0.5 #1 + 0.5 #2 + Normalize[Cross[#2 - #1]] 0.2 &], ImageSize -> 400]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/02242a8a7a86baf1.png) |
| Out[62]= | 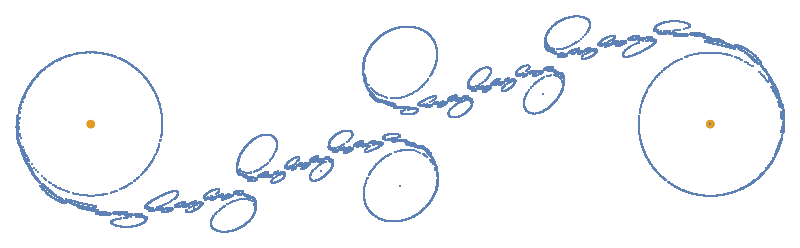 |
Excluding a wolf-shaped portion of the domain results in a fractal of wolves:
| In[63]:= | ![reg = \!\(\*
GraphicsBox[
TagBox[
DynamicModuleBox[{Typeset`mesh = HoldComplete[
BoundaryMeshRegion[CompressedData["
1:eJxFVgk4lGsbVrb2lZAQSQspnaIoj9KiqKyRUqmoo46liAhRSVki+76MPTGD
wVjmMWMmxjpKJR1rhUq7UqeT/nf8/fPPdc0111zv9z3f89z3/dz3p3zCxdxh
qoiISCr5Cn7dv899JXPmAfqFMs7uGWpH+5d8Ffn5HVhdGSZheo+PLf5GuIbX
gVasvCxtViteM9uTMrK2DadtTbKy3s9HNYmAGMPVHajxNa5nWXIzOom4BES/
acGSlPe5jk5t6E/qHgrh41T1G4vme/LQtDjawSC3GS1JPcVNLZiauYyxxb0d
te/qW/uc7kDa8hdXe7va8emxiwcmzBpQ52jVntETTTj+wj7jsXgTLoL7f2+0
a8UgniWrS7IeT663WjcjqQ2p0Q7BbzS4qDC7f028Ig/jp8mnhj9sQJ6xzk17
pRa0mzD8hztYh6I14gt2dDegnkZn4q4MLr5yUv/6PuY+9h4Ii5twrkdNB7nB
SgoPpfk7ugy0GOhjk7cxbKAJTzuSj08ttsmZdSeZcTHgwq7o8i0s5Le0tJiI
leDdhfwd8emN6Oj/dOulqFL0YqYtdvFsQZH1Q0XLLVJQoe7wUpZfK2YOKeSO
jMXism0fT84K5uHmxeTAg4o9Z0RcWDwOmndEHpmYU4QyTvs+v3Pl4w+toaJs
FTpSynS+qazgY7G+9WFaVwaGKp18V1XFx31JVml3YyNwFTso1zqSi0btjo+G
m+/hPOa6hNef6tBq1lR1SdVENDVYaG/4rRxb0xav7XG9hmsNl7zJTGShbEWH
iGIJC0Me9PaHdCOGnRv+kb+DOdl/sWYd3hp79mTbURZGaXmuUf7FQHrjRebu
2RzcrflLuUeKiQNut8JfODQie/OyvfLDZehD7vP3rcXnayLSvZLL8DrBaWh/
GXqciXz7bxgdRwneMssZk3jJutah0Z8uH66Ll03OH0CrQ+nkPzI3uBQjU3yB
FEqU41KzbvlkgxyUpNzRDfAvRxG5C0/WD1WiRvO8Bl1pOiZ5Jmd+bmRjiIeb
/D4qA6P9fujOW9mALpQpNV+SqRigxg5Ku8bCtprnUrXGdNwZcm5Y7zV3Evf0
7Dw8/WjYydigDqXEDs5ZM0ydxNthBgsTI+Z6ly8rw29xPVGnCzkY/fYyWM1P
xySiq3fjtVgaGzFXVzwfC7L2G0QR3TBEh0NXjoVN6mSXSzXqL/eYunhLupAH
xrqE1bLWUWBHw1HmOja6VZMC7vawgUPTTCXzLJ/kLQwPbS5r1E4rRfOUK2rs
p+lg/Tw76YUK4g3qwKuYnnwoNT2b6NlP/c0PFcL3vhYbO1aDh07p9bVL0kGO
6NbVsHCSH98PFcClaTqLpjDQ+cN1XufSWmicKPH5xM3BxalHVxmXIEzIXniy
oLsct+uPPB1NZoOIys+vX+zKkdEtf9n+hAOYbxIIdAdmXWpYpasYhApKY+cO
UuLQaBUh4JMXXr3MLz00PQWDCe6uJinoL1jklnSciPD7UeVZAYNMX4VNksdA
MG5VZx3kEPmp8igYGue8QDSmGmgEv4VpSehKZHTethR6spM4S3VjYDHR5dEm
Onw5d9C3SCcDj8kN2shoFmCWGPe2lt41DJL4sKixqBB1rlQYqMiUocm12Qdc
8u+DM5GvliUNrZvWcz7Sm4Cs+VAKLxmDw198UprfAnsJroEq9/DUPJvN7uw2
qDw7/Xt6cu7//AcC65oyxG9l4Za+A2FPdvOBRdo/nRWL0V8ljnV18MBEOnSv
k2cGEnaCTpu2wYOMneWfS69h3n1jnT0WXLBakX5znX8EEnibI+40wKm/d4l6
ZcdgiyQxTO8imEL8i65xHQa9pYoaXlXgvJ9fPY7nBMBoTMmsVd0sHCeDtPcm
Qf6IkWaxHBtP0KV/hHxOBnXZmM6bJyoxiNiLjbw/JvRE3RB3q8D5RbsHnAzo
MNA/M2pbFxsLiUzMRasg9Y/MsgaZejQU9ZoplcgAYm/Od3ZWoXml4nWfs1So
NY9VnmPJwNIwiQ/aHrngqNd3YOMhNnp4Z2tc9aWCariHW3U8G5vtjBsbptKB
wG3EbyF7S/z5aF4uuJO+jJ9VYl1e1v7jWkyIXy0bY8mswuKC9kcHz4QC/fPP
Tq+1xVjg84lqah8L2QSPefW3MYTQ8ICW8xu3aAxY9LRtfDsFzhN9SnVR0Uog
xLPFIEHW6S/ZEjRRXOS07wcVLq5RVhrzysevrwhQD12RyJoyRaoe+on/jI40
ghnxTUcrDhaFPDtzfG8zzFFd6TcazUGl3BGjg6dYMNAQX71IpxoF/OneZ8KR
oE2P91nXo7tq3K8IDgvkSBsPY+vx2Xc/p3+L62E1yYGu4urJvRBT48BjdQc5
28f1uMBmc5nXjfsQRfTeL82Z9Es7nQ7YteTNoJ8FF8//N09B1CVATDyKizPp
OZd+veHDd+Iju9PZuGfAW6qtrw16SIBIHUb0ydYw7LzbCs0XmWnnOzmY3cec
kyXBh5sk374t5GI6gclXjgYWAgEGJeBf8rP77xmUQD3JIflAsm8kj68EV4A+
eX75SB7OJH4z4xcbZNUsxClSaRh547qtBb8GWh8dHF0bTENi8zMXzmKBD5G1
WHI5dhN56o1zYeP7TTt3W91FAX3n3jeCIIcVI0rRm+RfynAzND5Ud0jwYOD4
NAJsoTEYfQ63GCugAEdAhBcFCCtuGh9oIKHAewnH4yCxliWjVhEJAh/VtiyE
1Udus7+oF8Jg6Mq3YR9zYND2Yc3zLS7YayNTYaZQBWHExzbIRAivFzx3Nq0E
hOcW7qrWpaW/5w4DMrXa4Eu28PnHJEkyq1UL739E+FLZVgeHyYuDslYWOBYc
t1w/rQHqyfrkRSZBF8V164xxjrC+N9H9wyQuPBIsSkIBjFFNz9rK8YT1+qZO
v6VkUgFbNx6teipRB9LEn3r/8RX2r0FiXpWRK6wnvmG+9pJb/+9n570/e7WG
q4Xn9NcX6Btv8OAUiT0xeikIcqJArxVWEL/quUKFwAqDwMDVzcLrP9pu148/
3woZGoZL1F+VQypnKfWBSbvwXH/GE4orlSX8H+sQfPJnER/+A7mLJaw=
"], { Line[{{1, 2}, {2, 9}, {9, 4}, {4, 6}, {6, 8}, {8, 11}, {11, 14}, {14, 16}, {16, 17}, {17, 20}, {20, 36}, {36, 45}, {45,
47}, {47, 49}, {49, 52}, {52, 54}, {54, 57}, {57, 66}, {
66, 58}, {58, 60}, {60, 62}, {62, 64}, {64, 72}, {72, 70}, {70, 73}, {73, 87}, {87, 132}, {132, 134}, {134, 136}, {136, 123}, {123, 104}, {104, 103}, {103, 67}, {67, 68}, {68, 69}, {69, 75}, {75, 76}, {76, 102}, {102, 105}, {
105, 106}, {106, 107}, {107, 124}, {124, 125}, {125, 127}, {127, 128}, {128, 114}, {114, 111}, {111, 101}, {101,
95}, {95, 99}, {99, 96}, {96, 100}, {100, 91}, {91, 88}, {
88, 92}, {92, 31}, {31, 43}, {43, 42}, {42, 39}, {39, 44}, {44, 38}, {38, 50}, {50, 35}, {35, 33}, {33, 34}, {34,
40}, {40, 41}, {41, 30}, {30, 25}, {25, 21}, {21, 22}, {
22, 27}, {27, 26}, {26, 28}, {28, 23}, {23, 24}, {24, 29}, {29, 32}, {32, 89}, {89, 90}, {90, 97}, {97, 98}, {98,
93}, {93, 94}, {94, 112}, {112, 113}, {113, 115}, {115, 116}, {116, 109}, {109, 110}, {110, 121}, {121, 122}, {122,
117}, {117, 118}, {118, 119}, {119, 120}, {120, 131}, {
131, 130}, {130, 129}, {129, 126}, {126, 148}, {148, 137}, {137, 149}, {149, 139}, {139, 150}, {150, 157}, {157,
145}, {145, 152}, {152, 155}, {155, 158}, {158, 156}, {
156, 153}, {153, 154}, {154, 146}, {146, 143}, {143, 144}, {144, 140}, {140, 71}, {71, 108}, {108, 85}, {85, 86}, {86, 83}, {83, 79}, {79, 84}, {84, 82}, {82, 81}, {81,
80}, {80, 78}, {78, 77}, {77, 65}, {65, 63}, {63, 61}, {
61, 59}, {59, 55}, {55, 56}, {56, 53}, {53, 51}, {51, 48}, {48, 46}, {46, 37}, {37, 18}, {18, 19}, {19, 15}, {15,
12}, {12, 13}, {13, 10}, {10, 7}, {7, 5}, {5, 3}, {3, 1}}]}, { Line[{{151, 142}, {142, 141}, {141, 74}, {74, 133}, {133, 135}, {135, 138}, {138, 147}, {147, 151}}]}, Method -> {"EliminateUnusedCoordinates" -> True, "DeleteDuplicateCoordinates" -> Automatic, "DeleteDuplicateCells" -> Automatic, "VertexAlias" -> Identity, "CheckOrientation" -> Automatic,
"CoplanarityTolerance" -> Automatic, "CheckIntersections" -> Automatic, "BoundaryNesting" -> {{0, 0}, {1, 1}}, "SeparateBoundaries" -> False, "TJunction" -> Automatic, "PropagateMarkers" -> True, "ZeroTest" -> Automatic, "Hash" -> 1353245008140257744}]]},
TagBox[GraphicsComplexBox[CompressedData["
1:eJxFVgk4lGsbVrb2lZAQSQspnaIoj9KiqKyRUqmoo46liAhRSVki+76MPTGD
wVjmMWMmxjpKJR1rhUq7UqeT/nf8/fPPdc0111zv9z3f89z3/dz3p3zCxdxh
qoiISCr5Cn7dv899JXPmAfqFMs7uGWpH+5d8Ffn5HVhdGSZheo+PLf5GuIbX
gVasvCxtViteM9uTMrK2DadtTbKy3s9HNYmAGMPVHajxNa5nWXIzOom4BES/
acGSlPe5jk5t6E/qHgrh41T1G4vme/LQtDjawSC3GS1JPcVNLZiauYyxxb0d
te/qW/uc7kDa8hdXe7va8emxiwcmzBpQ52jVntETTTj+wj7jsXgTLoL7f2+0
a8UgniWrS7IeT663WjcjqQ2p0Q7BbzS4qDC7f028Ig/jp8mnhj9sQJ6xzk17
pRa0mzD8hztYh6I14gt2dDegnkZn4q4MLr5yUv/6PuY+9h4Ii5twrkdNB7nB
SgoPpfk7ugy0GOhjk7cxbKAJTzuSj08ttsmZdSeZcTHgwq7o8i0s5Le0tJiI
leDdhfwd8emN6Oj/dOulqFL0YqYtdvFsQZH1Q0XLLVJQoe7wUpZfK2YOKeSO
jMXism0fT84K5uHmxeTAg4o9Z0RcWDwOmndEHpmYU4QyTvs+v3Pl4w+toaJs
FTpSynS+qazgY7G+9WFaVwaGKp18V1XFx31JVml3YyNwFTso1zqSi0btjo+G
m+/hPOa6hNef6tBq1lR1SdVENDVYaG/4rRxb0xav7XG9hmsNl7zJTGShbEWH
iGIJC0Me9PaHdCOGnRv+kb+DOdl/sWYd3hp79mTbURZGaXmuUf7FQHrjRebu
2RzcrflLuUeKiQNut8JfODQie/OyvfLDZehD7vP3rcXnayLSvZLL8DrBaWh/
GXqciXz7bxgdRwneMssZk3jJutah0Z8uH66Ll03OH0CrQ+nkPzI3uBQjU3yB
FEqU41KzbvlkgxyUpNzRDfAvRxG5C0/WD1WiRvO8Bl1pOiZ5Jmd+bmRjiIeb
/D4qA6P9fujOW9mALpQpNV+SqRigxg5Ku8bCtprnUrXGdNwZcm5Y7zV3Evf0
7Dw8/WjYydigDqXEDs5ZM0ydxNthBgsTI+Z6ly8rw29xPVGnCzkY/fYyWM1P
xySiq3fjtVgaGzFXVzwfC7L2G0QR3TBEh0NXjoVN6mSXSzXqL/eYunhLupAH
xrqE1bLWUWBHw1HmOja6VZMC7vawgUPTTCXzLJ/kLQwPbS5r1E4rRfOUK2rs
p+lg/Tw76YUK4g3qwKuYnnwoNT2b6NlP/c0PFcL3vhYbO1aDh07p9bVL0kGO
6NbVsHCSH98PFcClaTqLpjDQ+cN1XufSWmicKPH5xM3BxalHVxmXIEzIXniy
oLsct+uPPB1NZoOIys+vX+zKkdEtf9n+hAOYbxIIdAdmXWpYpasYhApKY+cO
UuLQaBUh4JMXXr3MLz00PQWDCe6uJinoL1jklnSciPD7UeVZAYNMX4VNksdA
MG5VZx3kEPmp8igYGue8QDSmGmgEv4VpSehKZHTethR6spM4S3VjYDHR5dEm
Onw5d9C3SCcDj8kN2shoFmCWGPe2lt41DJL4sKixqBB1rlQYqMiUocm12Qdc
8u+DM5GvliUNrZvWcz7Sm4Cs+VAKLxmDw198UprfAnsJroEq9/DUPJvN7uw2
qDw7/Xt6cu7//AcC65oyxG9l4Za+A2FPdvOBRdo/nRWL0V8ljnV18MBEOnSv
k2cGEnaCTpu2wYOMneWfS69h3n1jnT0WXLBakX5znX8EEnibI+40wKm/d4l6
ZcdgiyQxTO8imEL8i65xHQa9pYoaXlXgvJ9fPY7nBMBoTMmsVd0sHCeDtPcm
Qf6IkWaxHBtP0KV/hHxOBnXZmM6bJyoxiNiLjbw/JvRE3RB3q8D5RbsHnAzo
MNA/M2pbFxsLiUzMRasg9Y/MsgaZejQU9ZoplcgAYm/Od3ZWoXml4nWfs1So
NY9VnmPJwNIwiQ/aHrngqNd3YOMhNnp4Z2tc9aWCariHW3U8G5vtjBsbptKB
wG3EbyF7S/z5aF4uuJO+jJ9VYl1e1v7jWkyIXy0bY8mswuKC9kcHz4QC/fPP
Tq+1xVjg84lqah8L2QSPefW3MYTQ8ICW8xu3aAxY9LRtfDsFzhN9SnVR0Uog
xLPFIEHW6S/ZEjRRXOS07wcVLq5RVhrzysevrwhQD12RyJoyRaoe+on/jI40
ghnxTUcrDhaFPDtzfG8zzFFd6TcazUGl3BGjg6dYMNAQX71IpxoF/OneZ8KR
oE2P91nXo7tq3K8IDgvkSBsPY+vx2Xc/p3+L62E1yYGu4urJvRBT48BjdQc5
28f1uMBmc5nXjfsQRfTeL82Z9Es7nQ7YteTNoJ8FF8//N09B1CVATDyKizPp
OZd+veHDd+Iju9PZuGfAW6qtrw16SIBIHUb0ydYw7LzbCs0XmWnnOzmY3cec
kyXBh5sk374t5GI6gclXjgYWAgEGJeBf8rP77xmUQD3JIflAsm8kj68EV4A+
eX75SB7OJH4z4xcbZNUsxClSaRh547qtBb8GWh8dHF0bTENi8zMXzmKBD5G1
WHI5dhN56o1zYeP7TTt3W91FAX3n3jeCIIcVI0rRm+RfynAzND5Ud0jwYOD4
NAJsoTEYfQ63GCugAEdAhBcFCCtuGh9oIKHAewnH4yCxliWjVhEJAh/VtiyE
1Udus7+oF8Jg6Mq3YR9zYND2Yc3zLS7YayNTYaZQBWHExzbIRAivFzx3Nq0E
hOcW7qrWpaW/5w4DMrXa4Eu28PnHJEkyq1UL739E+FLZVgeHyYuDslYWOBYc
t1w/rQHqyfrkRSZBF8V164xxjrC+N9H9wyQuPBIsSkIBjFFNz9rK8YT1+qZO
v6VkUgFbNx6teipRB9LEn3r/8RX2r0FiXpWRK6wnvmG+9pJb/+9n570/e7WG
q4Xn9NcX6Btv8OAUiT0xeikIcqJArxVWEL/quUKFwAqDwMDVzcLrP9pu148/
3woZGoZL1F+VQypnKfWBSbvwXH/GE4orlSX8H+sQfPJnER/+A7mLJaw=
"],
{Hue[0.6, 0.3, 0.95], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[FilledCurveBox[{{Line[{1, 2, 9, 4, 6, 8, 11, 14, 16, 17, 20, 36, 45, 47, 49, 52, 54, 57, 66, 58, 60, 62, 64, 72, 70,
73, 87, 132, 134, 136, 123, 104, 103, 67, 68, 69, 75, 76, 102, 105, 106, 107, 124, 125, 127, 128, 114, 111, 101, 95, 99, 96, 100, 91, 88, 92, 31, 43, 42, 39, 44, 38, 50, 35, 33, 34, 40, 41, 30, 25, 21, 22, 27, 26, 28,
23, 24, 29, 32, 89, 90, 97, 98, 93, 94, 112, 113, 115,
116, 109, 110, 121, 122, 117, 118, 119, 120, 131, 130,
129, 126, 148, 137, 149, 139, 150, 157, 145, 152, 155,
158, 156, 153, 154, 146, 143, 144, 140, 71, 108, 85, 86, 83, 79, 84, 82, 81, 80, 78, 77, 65, 63, 61, 59, 55,
56, 53, 51, 48, 46, 37, 18, 19, 15, 12, 13, 10, 7, 5, 3}]}, {Line[{151, 142, 141, 74, 133, 135, 138, 147}]}}],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics",
AutoDelete->True,
Editable->False,
Selectable->False],
DefaultBaseStyle->{"MeshGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
ImageSize->{84.734375, Automatic}]\);
pts = ResourceFunction["GeneralizedChaosGame"][4, 10^5, Automatic, "List", "ExclusionRegionFunction" -> Function[{x, y}, RegionMember[reg][{x, y}]]];
Graphics[{White, PointSize[0.001], Point[pts]}, Background -> Black, PlotRange -> 0.8]](https://www.wolframcloud.com/obj/resourcesystem/images/f5a/f5a7e324-1480-41c0-a447-7dcb1683302e/2181cbeece7ddffa.png) |
| Out[65]= |  |
Perform a halfway step and a perpendicular step of 0.1:
| In[66]:= |
| Out[66]= | 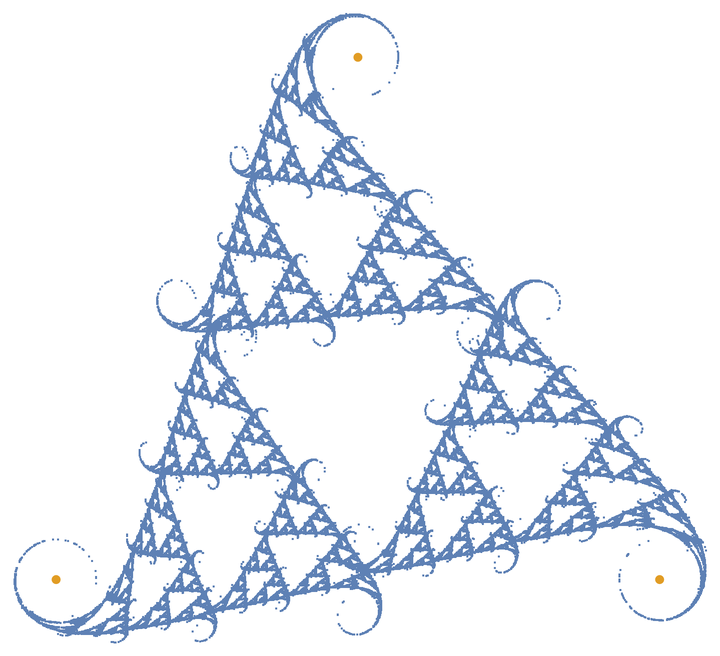 |
Perform a halfway step and a scaled perpendicular step:
| In[67]:= |
| Out[67]= |  |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License