Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find a rational interpolation of a function defined parametrically
ResourceFunction["GeneralRationalInterpolation"][{fx,fy},{t,m,n},x,{t1,…,tm+n+1}]] gives the rational polynomial function of x, with numerator order m and denominator order n, that interpolates the curve with x and y coordinates fx and fy generated as a function of t, at the interpolation points t1,t2, …. | |
ResourceFunction["GeneralRationalInterpolation"][{fx,fy},{t,m,n},x,{t,t0,t1}] gives the rational interpolant with the interpolation points chosen automatically from the interval t0 to t1. |
An approximation to the function whose graph is the upper half-circle:
| In[1]:= |
| Out[1]= |
The error is quite large near the endpoints:
| In[2]:= |
| Out[2]= | 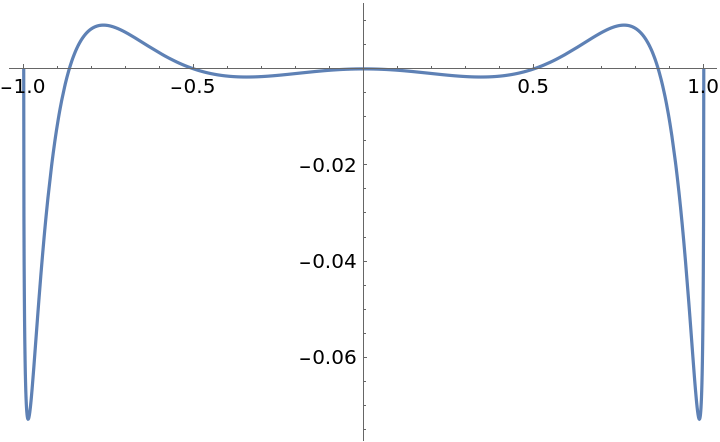 |
Automatically chosen the interpolation points result in a smaller maximum error:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= | 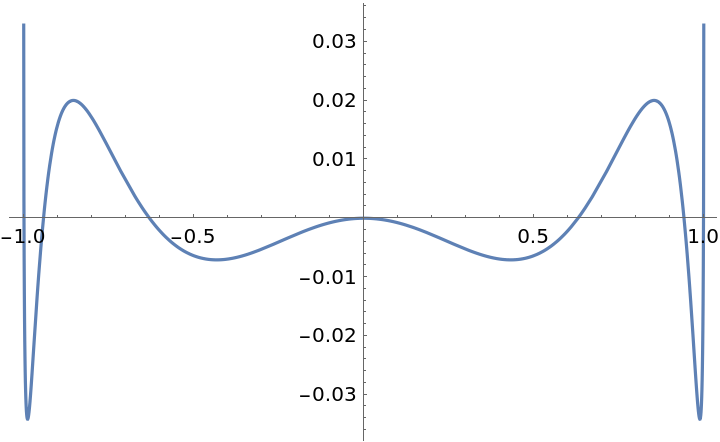 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License