Details and Options
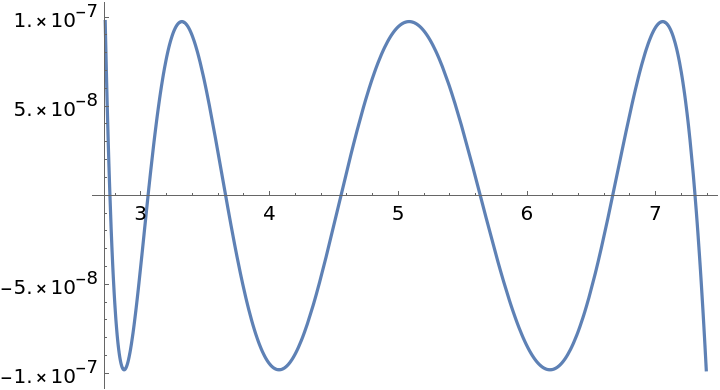
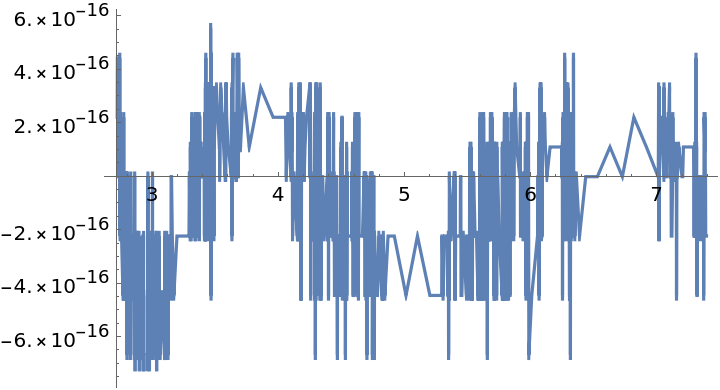
ResourceFunction["GeneralMiniMaxApproximation"] by default minimizes the maximum value of the relative error between the approximation and expr.
ResourceFunction["GeneralMiniMaxApproximation"][{fx,fy,g},{t,{t0,t1},m,n},x] computes the error using a factor of g. In this case, the mini-max approximation returned by ResourceFunction["GeneralMiniMaxApproximation"] is the rational function h[x] that minimizes the maximum value of the quantity (fy-h[fx])/g.
ResourceFunction["GeneralMiniMaxApproximation"] returns {abscissa,{approximation,maxerror}}, where abscissa is a list of the abscissas where the relative error is a local maximum, approximation is the rational approximant and maxerror is the global maximum of the relative error.
When an approximation is given as the second argument of ResourceFunction["GeneralMiniMaxApproximation"], it must have the same form as the result returned by ResourceFunction["GeneralMiniMaxApproximation"].
ResourceFunction["GeneralMiniMaxApproximation"] takes the same options as the resource function
MiniMaxApproximation.
In the "Derivatives" option, a list of derivatives must give derivatives for both parts of the parametrically-defined function.