Function Repository Resource:

GellMannMatrix

Source Notebook

Generalized Gell-Mann matrix

Contributed by: Nikolay Murzin and Mohammad Bahrami

ResourceFunction["GellMannMatrix"][n,i]

returns generalized i^th Gell-Mann matrix of dimension n.

ResourceFunction["GellMannMatrix"][n]

returns all n²-1 Gell-Mann matrices of dimension n.

Details and Options

Generalized Gell-Mann matrices are the n²-1 matrices that form the Lie algebra of the special unitary group SU(n) for n>=2. They extend the 3×3 Gell-Mann matrices for SU(3) and the 2×2 Pauli matrices for SU(2).

Generalized Gell-Mann matrices are traceless and Hermitian. Note that an equivalent mathematical convention defines SU(n) as traceless anti-Hermitian matrices; the two are related by X=iH. Under the Hermitian convention[X_a,X_b]=if_ab^cX_c while under the anti-Hermitian convention[X_a,X_b]=f_ab^cX_c with f_abc the structure constant.

ResourceFunction["GellMannMatrix"] can take TargetStructure as the option for constructing matrices. It includes the following choices:

Automatic

automatically choose the representation returned

"Dense"

represent the matrix as a dense array

"Sparse"

represent the matrix as a sparse array

"Structured"

represent the matrix as a structured array

The default value of TargetStructure is "Sparse". The option value Automatic corresponds to "Structured".

Examples

Basic Examples (2)

Construct generalized Gell-Mann matrices for n=4:

In[1]:=

Out[1]=

Construct the first generalized Gell-Mann matrices for n=5:

In[2]:=

Out[2]=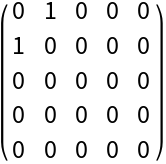

Scope (2)

Gell-Mann matrices are generator of SU(2):

In[3]:=

Out[3]=

The standard Gell-Mann matrices are 8 generators of SU(3):

In[4]:=

Out[4]=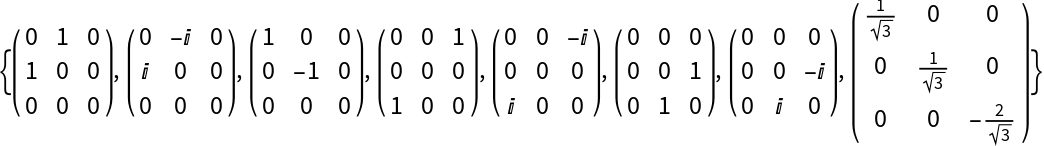

Options (2)

Gell-Mann matrices are given as sparse arrays by default:

In[5]:=

Out[5]=

Use the option TargetStructure to get them in different formats:

In[6]:=

Out[6]=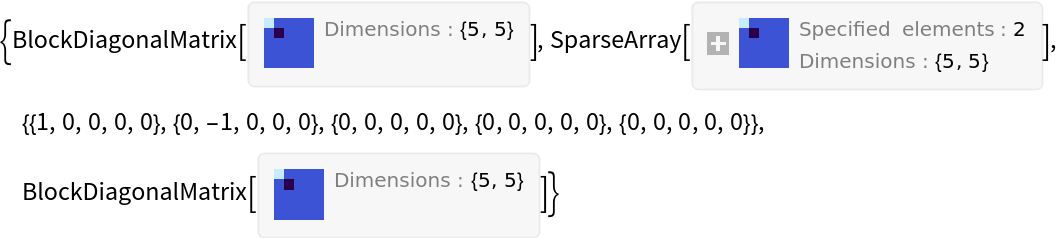

Properties and Relations (11)

Gell-Mann matrices of dimension 2 are the Pauli matrices:

In[7]:=

Out[7]=

Number of generalized Gell-Mann matrices is n²-1:

In[8]:=

$Table[Length@ResourceFunction["GellMannMatrix"][n] == n^2 - 1, {n, 2, 6}]$

Out[8]=

Gell-Mann matrices are Hermitian :

In[9]:=

Out[9]=

The matrices ⅈλ_i are anti-Hermitian:

In[10]:=

Out[10]=

Gell-Mann matrices are traceless Tr[λ_a]=0:

In[11]:=

Out[11]=

Gell-Mann matrices form an orthonormal set with respect to the Hilbert-Schmidt inner product, ie Tr[λ_iλ_j]=2δ_ij:

In[12]:=

$n = 4; d = n^2 - 1; \[ScriptCapitalG] = ResourceFunction["GellMannMatrix"][n]; Outer[Tr[#1 . #2] &, \[ScriptCapitalG], \[ScriptCapitalG], 1] == 2 IdentityMatrix[d]$

Out[14]=

Find the structure constants:

In[15]:=

$\[Lambda]n = ResourceFunction["GellMannMatrix"][4]; fabc = Outer[ 1/(4 I) Tr[(#1 . #2 - #2 . #1) . #3] &, \[Lambda]n, \[Lambda]n, \[Lambda]n, 1];$

In[16]:=

$dabc = Outer[ 1/4 Tr[(#1 . #2 + #2 . #1) . #3] &, \[Lambda]n, \[Lambda]n, \[Lambda]n, 1];$

Verify symmetric and antisymmetric features of structure constants:

In[17]:=

Out[17]=

In[18]:=

Out[18]=

Verify[λ_i,λ_j]=2ⅈ∑_kf_ijkλ_k:

In[19]:=

$\[Lambda]n = ResourceFunction["GellMannMatrix"][5]; fabc = Outer[ 1/(4 I) Tr[(#1 . #2 - #2 . #1) . #3] &, \[Lambda]n, \[Lambda]n, \[Lambda]n, 1]; Outer[#1 . #2 - #2 . #1 &, \[Lambda]n, \[Lambda]n, 1] == 2 I TensorContract[TensorProduct[fabc, \[Lambda]n], {{3, 4}}]$

Out[16]=

Verify :

In[20]:=

$n = 7; d = n^2 - 1; \[Lambda]n = ResourceFunction["GellMannMatrix"][n]; dabc = Outer[ 1/4 Tr[(#1 . #2 + #2 . #1) . #3] &, \[Lambda]n, \[Lambda]n, \[Lambda]n, 1]; Outer[#1 . #2 + #2 . #1 &, \[Lambda]n, \[Lambda]n, 1] == 4/n Outer[Times, IdentityMatrix[d], IdentityMatrix[n]] + 2 TensorContract[TensorProduct[dabc, \[Lambda]n], {{3, 4}}]$

Out[17]=

Verify product rule :

In[21]:=

$n = 5; d = n^2 - 1; \[Lambda]n = ResourceFunction["GellMannMatrix"][n]; fabc = Outer[ 1/(4 I) Tr[(#1 . #2 - #2 . #1) . #3] &, \[Lambda]n, \[Lambda]n, \[Lambda]n, 1]; dabc = Outer[ 1/4 Tr[(#1 . #2 + #2 . #1) . #3] &, \[Lambda]n, \[Lambda]n, \[Lambda]n, 1]; Outer[#1 . #2 &, \[Lambda]n, \[Lambda]n, 1] == 2/n Outer[Times, IdentityMatrix[d], IdentityMatrix[n]] + TensorContract[TensorProduct[dabc + I fabc, \[Lambda]n], {{3, 4}}]$