Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GaussianQuadratureMatrix

Source Notebook

Symmetric tridiagonal matrix for Gaussian quadrature

Contributed by: Paul Abbott (additional contributions by Wolfram Research staff)

ResourceFunction["GaussianQuadratureMatrix"][n]

returns the n×n symmetric tridiagonal matrix that determines the abscissas and weights of the Gaussian quadrature.

Details and Options

The abscissas and weights for the elementary n-point Gaussian quadrature formula are simply related to the eigenvalues and first component of the orthonormal eigenvectors of this matrix.

Examples

Basic Examples (1) 

Compute the symmetric tridiagonal matrix of size 6×6:

In[1]:=
ResourceFunction["GaussianQuadratureMatrix"][6]
Out[1]=
In[2]:=
% // MatrixForm
Out[2]=

Properties and Relations (3) 

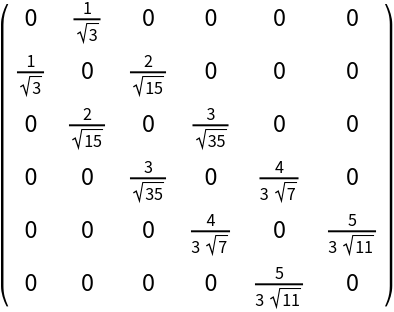The abscissas and weights for the elementary n-point Gaussian quadrature are related to the eigensystem of the n⨯n symmetric tridiagonal Gaussian quadrature matrix:

In[3]:=
n = 6;
In[4]:=
{xx, ww} = Transpose[ ResourceFunction["GaussianQuadratureWeights"][n, {-1, 1}]];
In[5]:=
(m = ResourceFunction["GaussianQuadratureMatrix"][n]) // MatrixForm
Out[5]=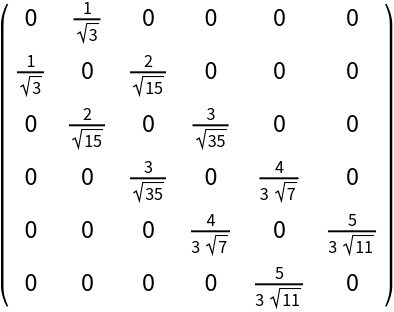

Eigenvalues of the matrix determine the abscissas:

In[6]:=
Eigenvalues[m] // NumericalSort
Out[6]=
In[7]:=
% - xx // Simplify
Out[7]=

Eigenvectors of the matrix determine the weights:

In[8]:=
{Eigenvalues[m], 2 (Normalize /@ Eigenvectors[m])[[All, 1]]^2} // Transpose // NumericalSort // Transpose;
In[9]:=
%[[2]] - ww // Simplify
Out[9]=

Version History

  • 1.0.0 – 06 November 2020

Related Resources

License Information