Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GaussianCurvature

Source Notebook

Compute the Gaussian curvature of a surface

Contributed by: Alfred Gray

ResourceFunction["GaussianCurvature"][s,{u,v}]

computes the Gaussian curvature of the surface s parameterized by u and v.

ResourceFunction["GaussianCurvature"][eq,{x,y,z}]

computes the Gaussian curvature of the surface s given by the implicit equation eq in variables x,y and z.

Details and Options

The Gaussian curvature is an intrinsic property of a space independent of the coordinate system used to describe that space.

Examples

Basic Examples (1) 

Compute the Gaussian curvature of a sphere:

In[1]:=
ResourceFunction["GaussianCurvature"][ Entity["Surface", "Sphere"]["ParametricEquations"][a][u, v], {u, v}]
Out[1]=

Scope (3) 

Plot an astroidal ellipsoid:

In[2]:=
ParametricPlot3D[ Evaluate[ Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][1, 1, 1][u, v]], {u, 0, 2 \[Pi]}, {v, -(\[Pi]/2), \[Pi]/2}, PlotPoints -> 50, PlotRange -> 1]
Out[2]=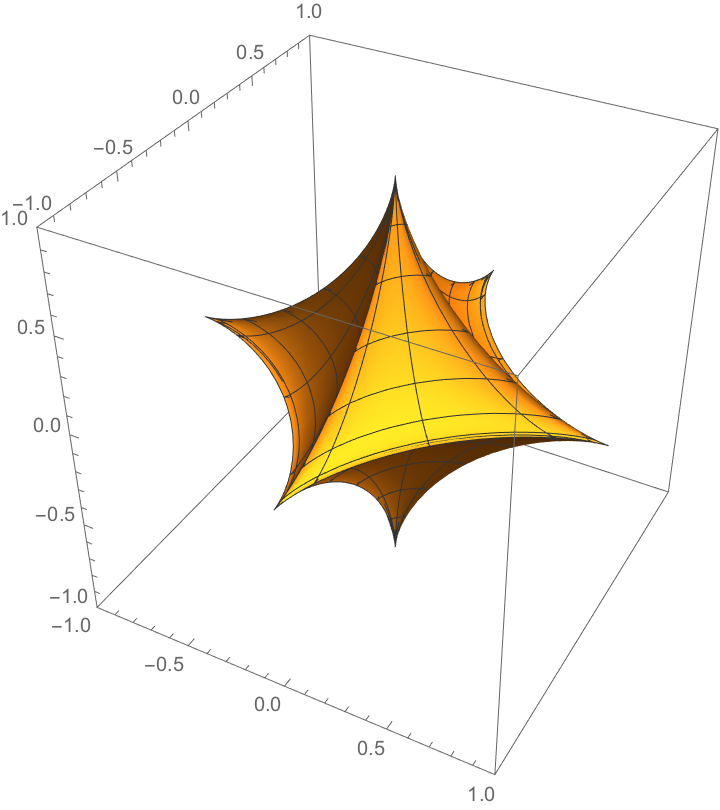

Now compute its Gaussian curvature:

In[3]:=
ResourceFunction["GaussianCurvature"][ Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][a, b, c][u, v], {u, v}]
Out[3]=

Plot the Gaussian curvature:

In[4]:=
Plot3D[Evaluate[ ResourceFunction["GaussianCurvature"][ Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][1, 1, 1][u, v], {u, v}]], {u, 0, 2 \[Pi]}, {v, -(\[Pi]/2), \[Pi]/2}, PlotRange -> {{0, 2 \[Pi]}, {-(\[Pi]/2), \[Pi]/2}, {0, 150}}, PlotPoints -> 50]
Out[4]=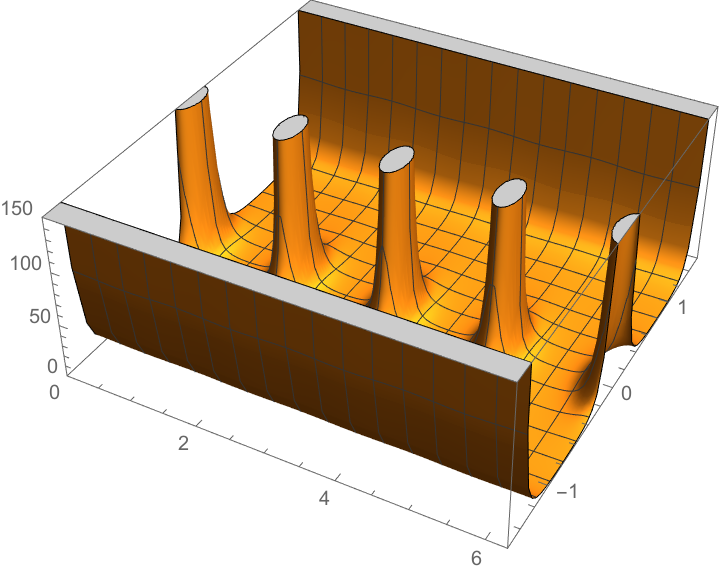

Define a Möbius strip:

In[5]:=
mobius = {Cos[v] (3 + u Cos[v/2]), Sin[v] (3 + u Cos[v/2]), u Sin[v/2]}
Out[5]=

Compute the Gaussian curvature:

In[6]:=
gcur = ResourceFunction["GaussianCurvature"][mobius, {u, v}]
Out[6]=

Plot the Gaussian curvature:

In[7]:=
curp = Plot3D[gcur, {u, -1.2, 1.2}, {v, 0, 2 Pi}, ColorFunction -> "TemperatureMap", PlotRange -> Full]
Out[7]=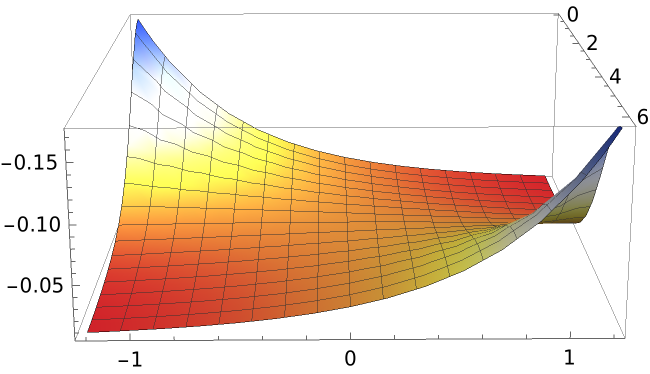

Plot the Möbius strip colored according to its Gaussian curvature:

In[8]:=
range = Last[ PlotRange /. AbsoluteOptions[curp, PlotRange]]; ParametricPlot3D[mobius, {u, -1.2, 1.2}, {v, 0, 2 Pi}, PlotRange -> All, Boxed -> False, PlotStyle -> Opacity[0.8], PlotPoints -> {80, 20}, Mesh -> 12, MeshFunctions -> Function[{x, y, z, u, v}, Rescale[gcur, range]], ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[gcur, range]]], ColorFunctionScaling -> False]
Out[8]=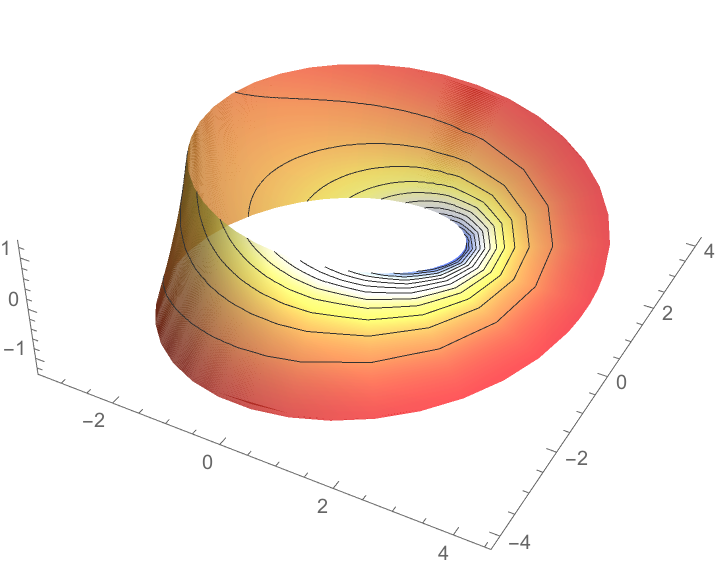

Here is an implicit equation for a surface:

In[9]:=
sinsurfaceimplicit[a_][x_, y_, z_] := 4 x^2 y^2 (a^2 - z^2) - a^2 (x^2 + y^2 - z^2)^2

Plot it:

In[10]:=
ContourPlot3D[ sinsurfaceimplicit[1][x, y, z] == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, PlotPoints -> 30]
Out[10]=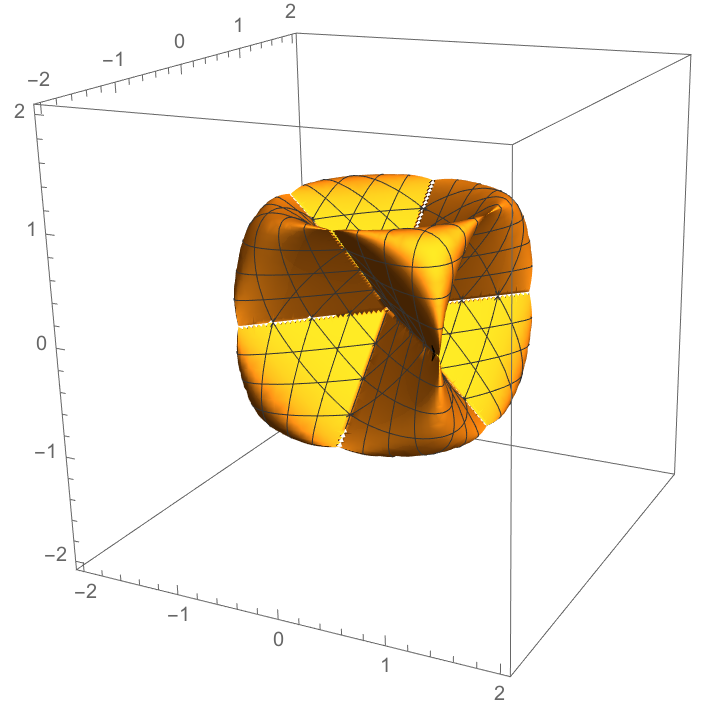

Compute its Gaussian curvature:

In[11]:=
ResourceFunction["GaussianCurvature"][ sinsurfaceimplicit[1][x, y, z], {x, y, z}]
Out[11]=

Properties and Relations (3) 

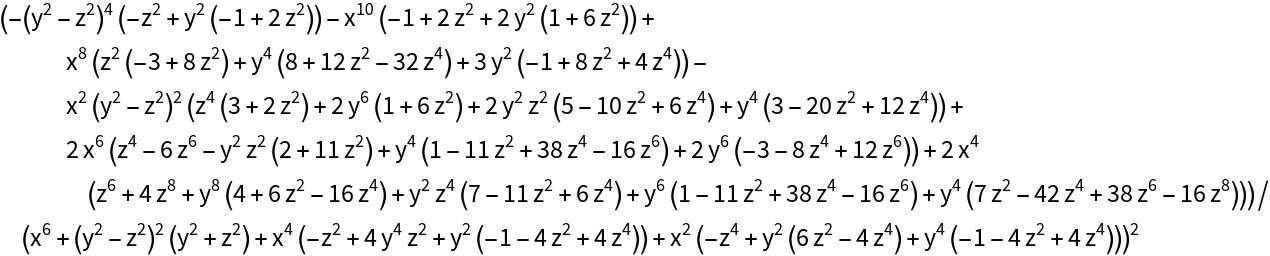The curvature can be obtained for named surfaces using entities:

In[12]:=
Entity["Surface", "AstroidalEllipsoid"][ EntityProperty["Surface", "GaussianCurvature"]][a, b, c][u, v]
Out[12]=

Here is the result returned by GaussianCurvature:

In[13]:=
ResourceFunction["GaussianCurvature"][ Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][a, b, c][u, v], {u, v}]
Out[13]=

The expressions seem to be different, but they are equal:

In[14]:=
FullSimplify[ Entity["Surface", "AstroidalEllipsoid"][ EntityProperty["Surface", "GaussianCurvature"]][a, b, c][u, v] - ResourceFunction["GaussianCurvature"][ Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][a, b, c][u, v], {u, v}]]
Out[14]=

Publisher

Enrique Zeleny

Version History

  • 2.1.0 – 04 January 2021
  • 2.0.0 – 01 April 2020
  • 1.0.0 – 13 February 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information