Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GaloisGroupProperties

Source Notebook

Compute the Galois group for a polynomial

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["GaloisGroupProperties"][poly,var]

returns the Galois group for a univariate polynomial poly in the variable var.

ResourceFunction["GaloisGroupProperties"][poly,var,prop]

returns the specified property prop.

Details and Options

ResourceFunction["GaloisGroupProperties"] typically supports only polynomials up to degree 4.
The property prop can be All, "Group", "GroupOrder", "Generators", "GroupElements", "MultiplicationTable" and "CayleyGraph". The default prop is "Group".

Examples

Basic Examples (1) 

Compute the Galois group of the polynomial x2+1:

In[1]:=
ResourceFunction["GaloisGroupProperties"][x^2 + 1, x]
Out[1]=

Scope (7) 

Compute the Galois group of the polynomial x4+2:

In[2]:=
ResourceFunction["GaloisGroupProperties"][x^4 + 2, x]
Out[2]=

Return the CayleyGraph for the Galois group:

In[3]:=
ResourceFunction["GaloisGroupProperties"][x^4 + 2, x, "CayleyGraph"]
In[4]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/f858d0b7-0bd9-4045-bc75-f9023638a388"]

Find the group order:

In[5]:=
ResourceFunction["GaloisGroupProperties"][x^4 + 2, x, "GroupOrder"]
Out[5]=

Get the generators:

In[6]:=
ResourceFunction["GaloisGroupProperties"][x^4 + 2, x, "Generators"]
Out[6]=

Find the group elements:

In[7]:=
ResourceFunction["GaloisGroupProperties"][x^4 + 2, x, "GroupElements"]
Out[7]=

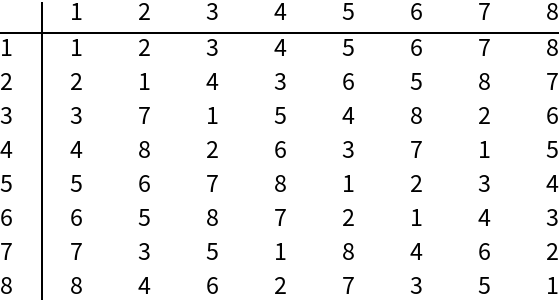
Display the group multiplication table:

In[8]:=
ResourceFunction["GaloisGroupProperties"][ x^4 + 2, x, "MultiplicationTable"]
Out[9]=

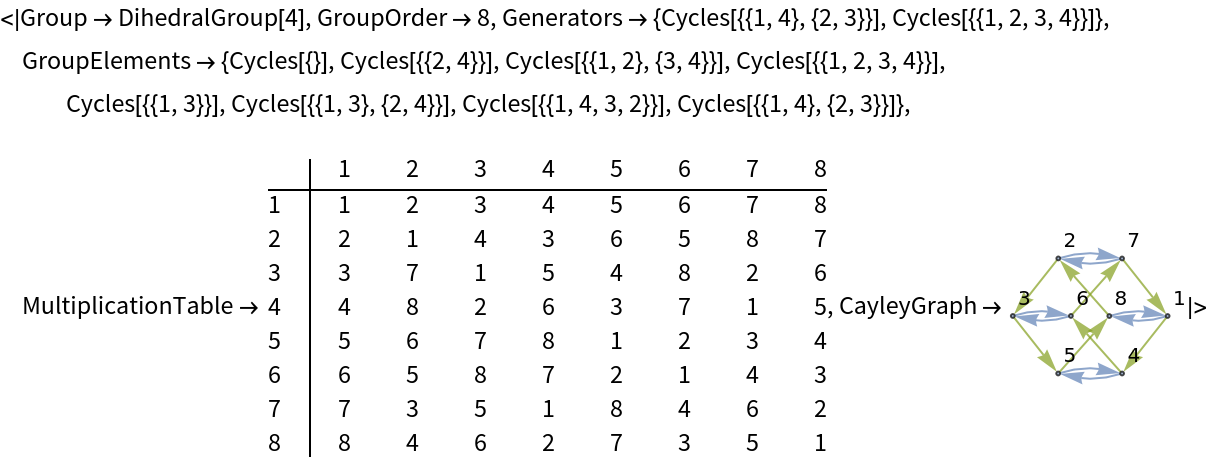
Get all of the available properties as an Association:

In[10]:=
ResourceFunction["GaloisGroupProperties"][x^4 + 2, x, All]
Out[10]=

Properties and Relations (2) 

An irreducible polynomial of prime degree p larger than 4 with exactly 2 nonreal roots has Galois group SymmetricGroup[p]:

In[11]:=
IrreduciblePolynomialQ[x^5 - 5 x + 2]
Out[11]=

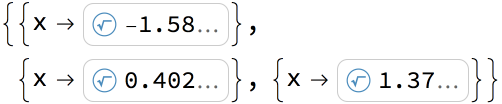
Verify that there are 3 real roots:

In[12]:=
Solve[x^5 - 5 x + 2 == 0, x, Reals]
Out[12]=

The Galois group for the irreducible polynomial of prime degree 5 with 2 nonreal roots is:

In[13]:=
ResourceFunction["GaloisGroupProperties"][x^5 - 5 x + 2, x]
Out[13]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 2.0.0 – 23 March 2023
  • 1.0.0 – 25 August 2020

Source Metadata

  • Citation:
    • Hungerford, T., Algebra, Springer, 2012.
      Dummit, D. and Foote, R., Abstract Algebra, 3rd Ed., Wiley, 2004.

Related Resources

Author Notes

To view the full source code for GaloisGroupProperties, run the following code:

FileNameJoin[ReplacePart[FileNameSplit[FindFile["ResourceFunctionHelpers`"]], -1 →"GaloisGroupProperties.wl"]] // SystemOpen

License Information