Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
The Gallai–Edmonds decomposition of a graph
ResourceFunction["GallaiEdmondsDecomposition"][g] gives the Gallai–Edmonds decomposition of the graph g. |
Define a graph g:
| In[1]:= |
| Out[1]= | 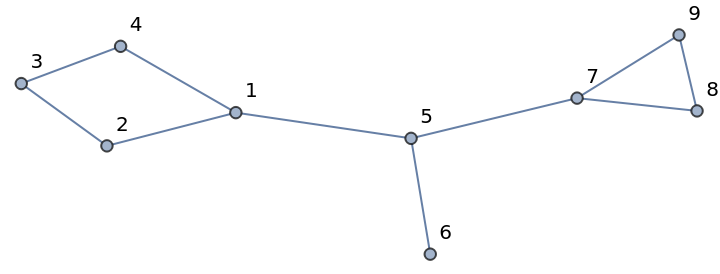 |
Find the Gallai-Edmonds decomposition of g:
| In[2]:= |
| Out[2]= |
Visualize it, with a maximum matching highlighted:
| In[3]:= |
| Out[3]= | 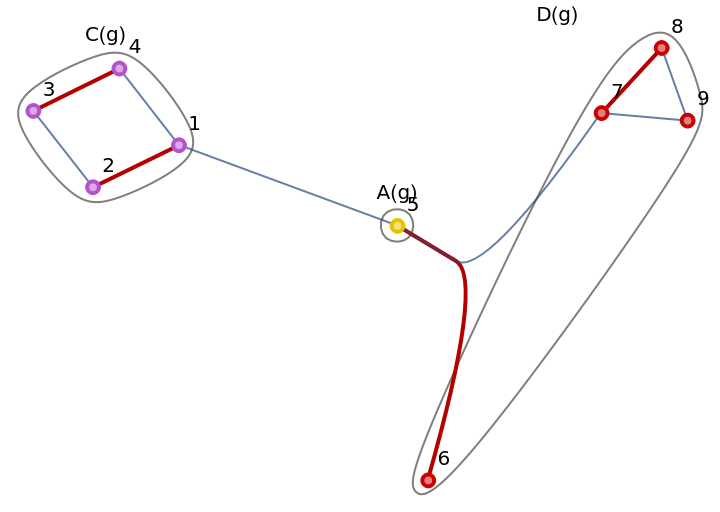 |
This work is licensed under a Creative Commons Attribution 4.0 International License