Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the fusc function
ResourceFunction["Fusc"][n] gives the fusc function fusc(n). |
Evaluate numerically for positive even integer input:
| In[1]:= |
| Out[1]= |
Evaluate numerically for positive odd integer input:
| In[2]:= |
| Out[2]= |
Plot Fusc over a subset of the non-negative integers:
| In[3]:= |
| Out[3]= | 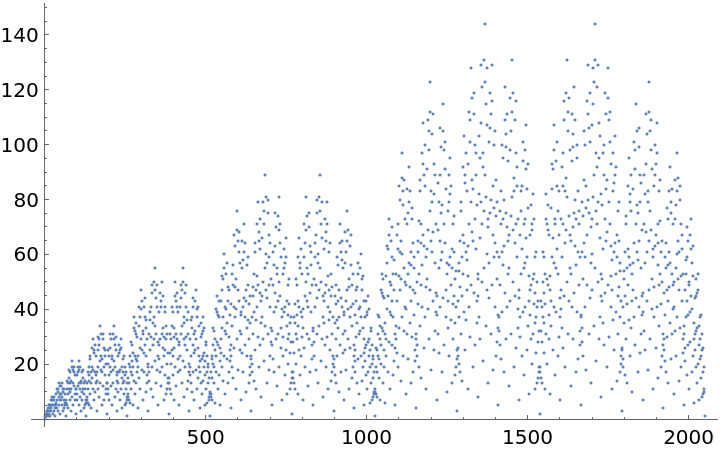 |
Fusc threads elementwise over lists:
| In[4]:= |
| Out[4]= |
The value fusc(n+1) is the number of odd binomial coefficients of the form Binomial[n-r,r], 0≤2r≤n:
| In[5]:= |
| Out[6]= |  |
| In[7]:= |
| Out[7]= |  |
Confirm the two lists are equal:
| In[8]:= |
| Out[8]= |
An alternative way to compute the same quantity:
| In[9]:= |
| Out[9]= |  |
Confirm all three are equal:
| In[10]:= |
| Out[10]= |
Fusc returns unevaluated if its input is anything other than a non-negative integer:
| In[11]:= |
| Out[11]= |
Generate the first 100 terms of Stern's diatomic series, also known as the Stern–Brocot sequence (OEIS A002487):
| In[12]:= |
| Out[12]= |  |
When used in conjunction with Prime, you can generate OEIS sequences A261179 and A261273:
| In[13]:= |
| Out[13]= |  |
| In[14]:= |
| Out[14]= |  |
These two sequences combine to form the prime numbered elements in the Calkin–Wilf sequence, one popular enumeration of the rational numbers. More precisely, the terms of the Calkin–Wilf enumeration of the rationals are given by fusc(n)/fusc(n+1):
| In[15]:= |
| Out[15]= | 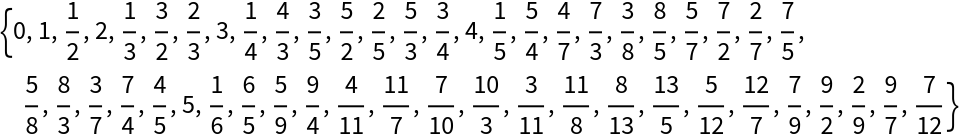 |
This work is licensed under a Creative Commons Attribution 4.0 International License