Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Determine the intervals on which a function is positive, negative or zero
ResourceFunction["FunctionSigns"][expr, x] returns an association of the values of x for which expr is positive, negative or zero. | |
ResourceFunction["FunctionSigns"][expr, x, prop] returns a property of expr related to regions where expr is positive, negative or zero. | |
ResourceFunction["FunctionSigns"][expr, x, {prop1, prop2, …}] returns an Association of the properties propi related to regions where expr is positive, negative or zero. | |
ResourceFunction["FunctionSigns"][expr, x, All] includes all available properties. |
Find the regions where x2-4 is positive, negative or zero:
| In[1]:= |
| Out[1]= |
Get several representations of information about the sign of x2-4:
| In[2]:= |
| Out[2]= | 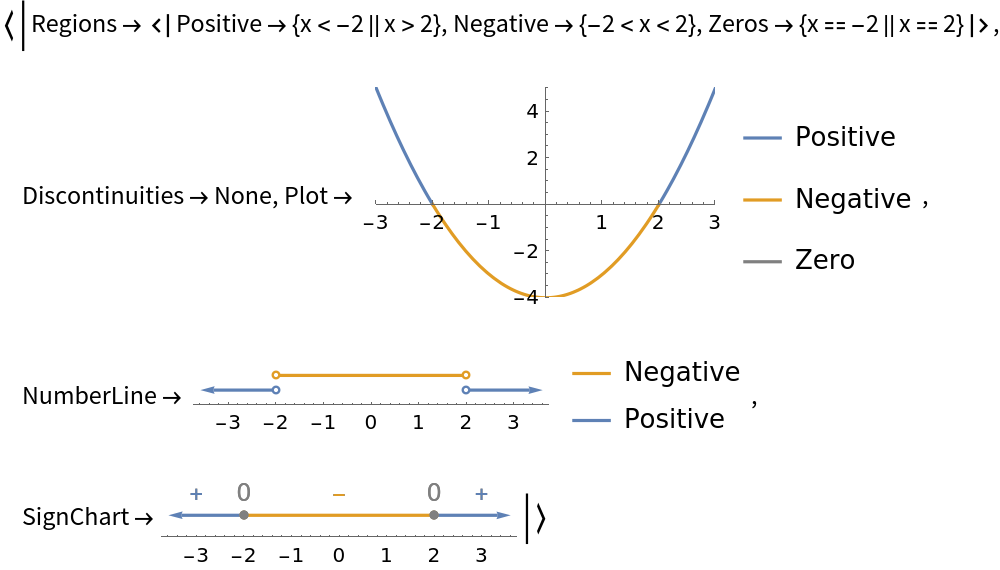 |
Get a plot of a function colored to correspond to the sign of the output of the function:
| In[3]:= |
| Out[3]= | 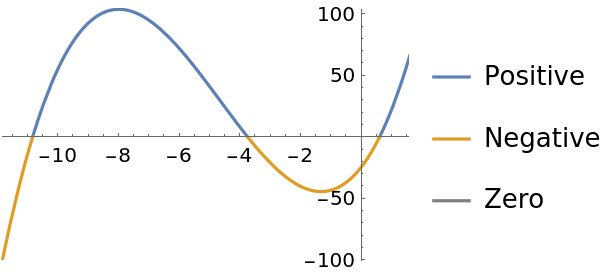 |
Get a sign chart that shows the intervals on which a function is positive, negative or zero:
| In[4]:= |
| Out[4]= | 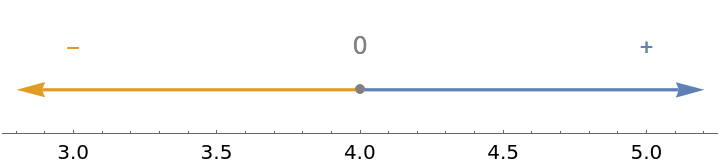 |
Discontinuities are indicated on the sign chart with vertical dots:
| In[5]:= |
| Out[5]= | 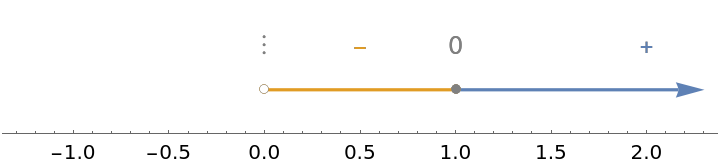 |
If there are infinitely many places where a function changes signs, the visual outputs of FunctionSigns display information for an interval surrounding x = 0:
| In[6]:= |
| Out[6]= | 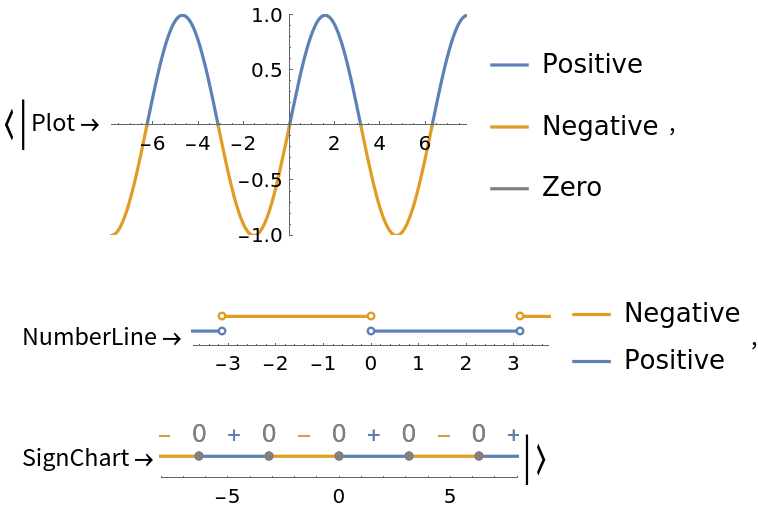 |
The function SignChart is available as a stand-alone resource function:
| In[7]:= |
| Out[7]= | 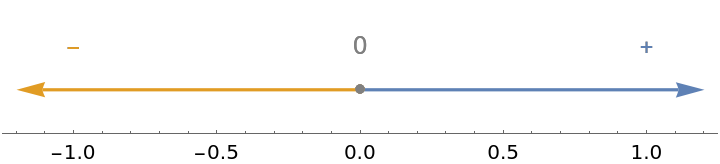 |
This work is licensed under a Creative Commons Attribution 4.0 International License