Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the discontinuities of a function of a single variable
ResourceFunction["FunctionDiscontinuities"][f,x] computes the values of x at which f(x) is discontinuous with respect to x. | |
ResourceFunction["FunctionDiscontinuities"][{f,cond},x] computes the x for which cond is True and f(x) is discontinuous with respect to x. | |
ResourceFunction["FunctionDiscontinuities"][…,x,"Properties"] computes points of discontinuity along with related information about each. |
Compute the points of discontinuity of a rational function:
| In[1]:= |
| Out[1]= |
Repeat the calculation, classifying the points of discontinuity:
| In[2]:= |
| Out[2]= |
Compute the points of discontinuity of a trigonometric function:
| In[3]:= |
| Out[3]= |
Repeat the calculation, classifying the points of discontinuity:
| In[4]:= |
| Out[4]= | 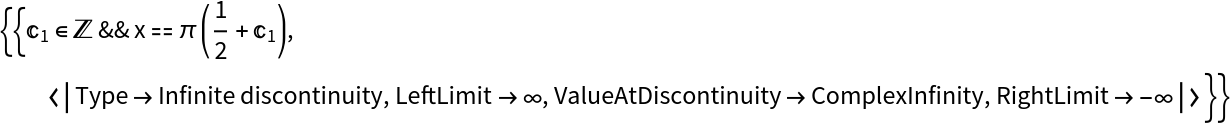 |
Compute the points of discontinuity of a smooth function:
| In[5]:= |
| Out[5]= |
Compute and plot the points of discontinuity of a rational function:
| In[6]:= | ![f[x_] := (-12 - x + x^2)/(8 + 2 x - 5 x^2 + x^3);
ResourceFunction["FunctionDiscontinuities"][f[x], x, "Properties"]](https://www.wolframcloud.com/obj/resourcesystem/images/061/06174cf2-8e7f-4c84-980c-621f2627a740/0adf1211504272f6.png) |
| Out[7]= |  |
| In[8]:= |
| Out[8]= | 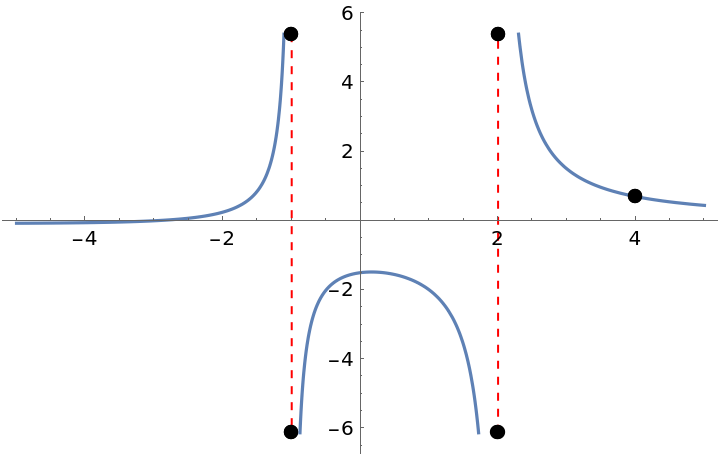 |
Compute and plot the points of discontinuity of a step function:
| In[9]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= | 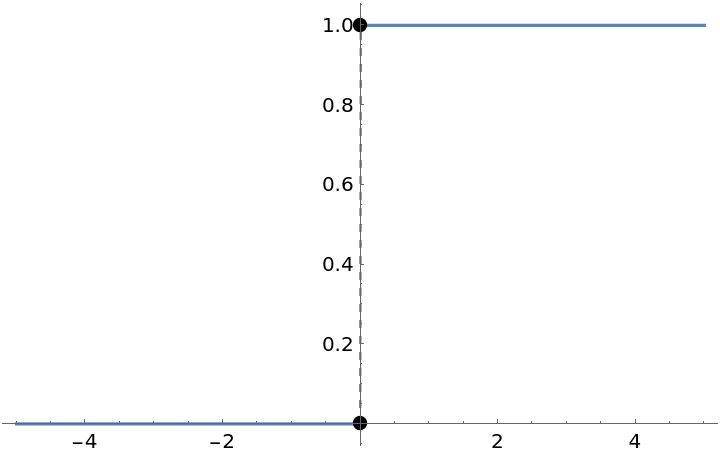 |
Compute and plot the points of discontinuity of a step function:
| In[12]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= | 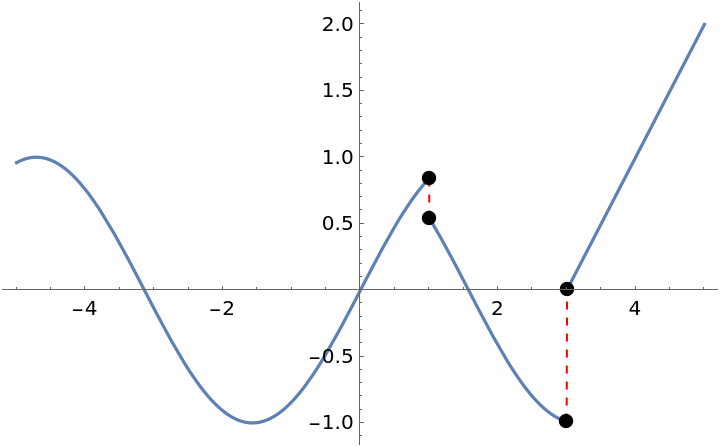 |
Choose whether to exclude removable singularities:
| In[15]:= | ![f[x_] := (x^3 + 8)/(x^3 + 3 x^2 - 4 x - 12);
Plot[f[x], {x, -5, 5}, ExclusionsStyle -> {{Red, Dashed}, {PointSize -> 0.02}}]](https://www.wolframcloud.com/obj/resourcesystem/images/061/06174cf2-8e7f-4c84-980c-621f2627a740/2d6e5696716db850.png) |
| Out[16]= | 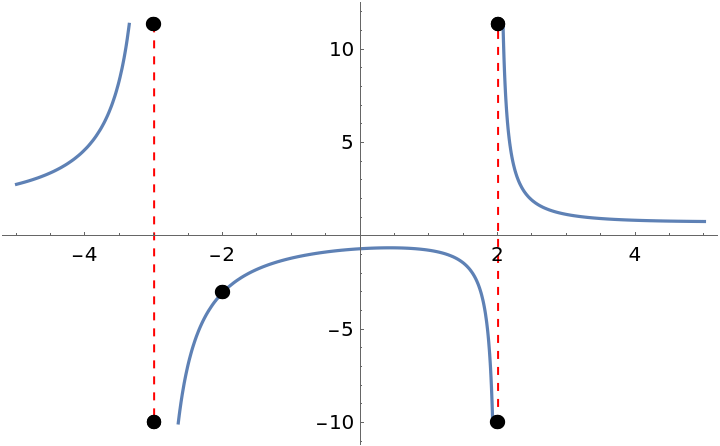 |
| In[17]:= |
| Out[17]= |
| In[18]:= |
| Out[18]= |
FunctionDiscontinuities has the attribute HoldFirst, enabling calculations such as the following:
| In[19]:= |
| Out[19]= |
Points where a function approaches ±∞ are considered to be points of discontinuity, even if they are technically outside the range of function definition:
| In[20]:= |
| Out[20]= |
This work is licensed under a Creative Commons Attribution 4.0 International License