Details and Options
ResourceFunction["FunctionAudiolize"] outputs a piece of audio such that the frequency at a particular moment is determined by the value of the plotted function for the corresponding value of the independent variable. The volume is constant.
ResourceFunction["FunctionAudiolize"] only accepts real-valued functions.
Frequency as a function of time,
f(t), is determined by
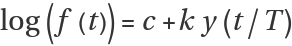
, where
y(x) is the plotted function and
k>=0,T>0. The higher the value of
y, the higher the frequency. If
y is negative and has a large absolute value, the frequency is low.
ResourceFunction["FunctionAudiolize"] can be useful to mathematicians/math enthusiasts who want to enhance their intuition about a particular function by converting it to audio; this especially applies to audials, people who perceive information better through hearing.
An audiolization can often be more intuitive than a regular plot. The ability to perceive functions through sound can potentially be tremendously helpful to sight-impaired people who want to learn math, but do not have access to the traditional teaching techniques that rely heavily on visual input.
ResourceFunction["FunctionAudiolize"] supports the following options:
| "BaselineFrequency" | 440 | average frequency of the audiolization, in hertz |
| "MinFrequency" | 120 | a lower bound below which the frequency is not allowed to fall, in hertz |
| "MaxFrequency" | 1910 | an upper bound above which the frequency is not allowed to rise, in hertz |
| "TimeStep" | 0.01 | time steps for discretization of the plotting domain |
| SampleRate | 8000 | SampleRate of ResourceFunction["FunctionAudiolize"]; determines the quality of sound |
The frequency cannot surpass "MinFrequency" and "MaxFrequency", but it is not obliged to touch both of these bounds. The frequency generally touches exactly one of those limits, either the upper or the lower one.
The mean value of
log(f(t)) over the length of the audio is bound to be equal to
Log["BaselineFrequency"].
ResourceFunction["FunctionAudiolize"] uses the built-in function
Play to make sounds. It computes the frequency as a function of time by rescaling the plotted function, finds the sound pressure as a piecewise sine function, and uses
Play.
![{ResourceFunction["FunctionAudiolize"][
Exp[-x/30] Cos[x], {x, 0, 20 \[Pi]}, 10], Plot[Exp[-x/30] Cos[x], {x, 0, 20 \[Pi]}]}](https://www.wolframcloud.com/obj/resourcesystem/images/429/4295065b-b82a-468a-8365-6b597b3d2e48/79e605d848ab3d85.png)

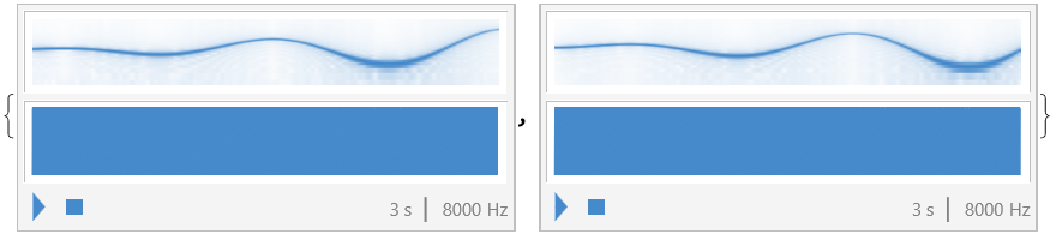
![With[{f = x Exp[I x]}, {ResourceFunction["FunctionAudiolize"][
Abs[f], {x, 0, 4 \[Pi]}, 3], ResourceFunction["FunctionAudiolize"][Arg[f], {x, 0, 4 \[Pi]}, 3]}]](https://www.wolframcloud.com/obj/resourcesystem/images/429/4295065b-b82a-468a-8365-6b597b3d2e48/03b29267803bca1d.png)

![With[{f = x Exp[I x]}, {ResourceFunction["FunctionAudiolize"][
Re[f], {x, 0, 4 \[Pi]}, 3], ResourceFunction["FunctionAudiolize"][Im[f], {x, 0, 4 \[Pi]}, 3]}]](https://www.wolframcloud.com/obj/resourcesystem/images/429/4295065b-b82a-468a-8365-6b597b3d2e48/64b1ee48e7ebc62c.png)
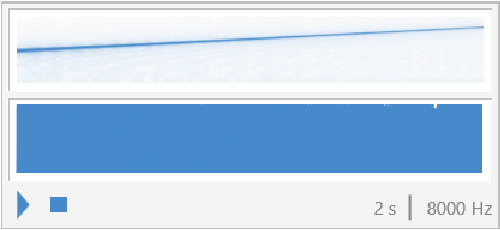
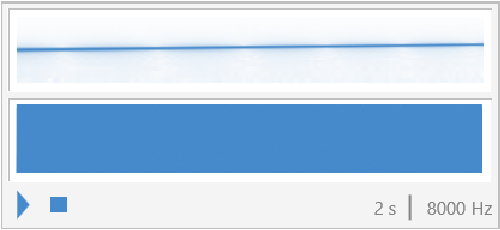
![{ResourceFunction["FunctionAudiolize"][
Tan[\[Phi]], {\[Phi], \[Pi]/2 - 0.5, \[Pi]/2 - 0.1}, 2, "TimeStep" -> 0.06], ResourceFunction["FunctionAudiolize"][
Tan[\[Phi]], {\[Phi], \[Pi]/2 - 0.5, \[Pi]/2 - 0.1}, 2]}](https://www.wolframcloud.com/obj/resourcesystem/images/429/4295065b-b82a-468a-8365-6b597b3d2e48/0d34543211f6199b.png)
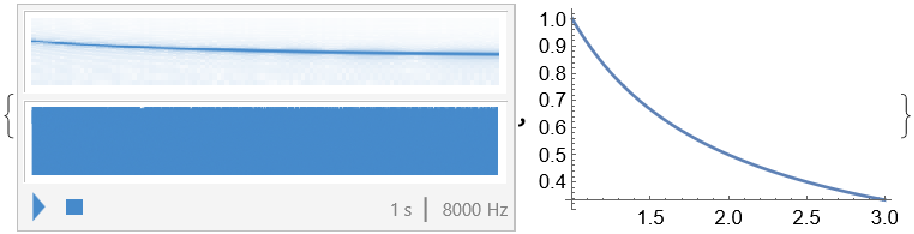
![{ResourceFunction["FunctionAudiolize"][Sin[x], {x, 0, \[Pi]}, 2], ResourceFunction["FunctionAudiolize"][
123 + 999 Sin[(x + 456)/100], {x, -456, 100 \[Pi] - 456}, 2]}](https://www.wolframcloud.com/obj/resourcesystem/images/429/4295065b-b82a-468a-8365-6b597b3d2e48/03dcf674ab4995b6.png)


![With[{n = 40}, ResourceFunction["FunctionAudiolize"][
Evaluate[Piecewise[
Table[{Mod[Fibonacci[i - 1], 17], i - 1 <= t < i}, {i, n}]]], {t, 0, n}, 5]]](https://www.wolframcloud.com/obj/resourcesystem/images/429/4295065b-b82a-468a-8365-6b597b3d2e48/6cf1a45d886f7128.png)
![Block[{notes = ({"C5", "B4", "G4", "E4", (**)"C5", "B4", "G4", "E4", (**)
"C5", "B4", "G4", "E4", (**)"C5", "B4", "G4", "E4", (**)"F4", "E4", "F4", "C4", (**)"F4", "E4", "F4", "C4", (**)"F4", "E4", "F4", "C4", (**)"F4", "E4", "F4", "C4", (**) "C5", "B4", "G4", "E4", (**) "C5", "B4", "G4", "E4", (**) "C5", "B4", "G4", "E4", (**) "C5", "B4", "G4", "E4", (**) "F4", "E4", "F4", "G4", (**) "A4", "G4", "A4", "B4", (**) "C5", "B4", "C5", "D5"} /. {"A4" -> 49, "B4" -> 51, "C5" -> 52, "G4" -> 47, "E4" -> 44, "F4" -> 45, "C4" -> 40, "D5" -> 54}) - 49, func}, func = Evaluate[
Piecewise[Table[{notes[[i]], i - 1 <= k < i}, {i, Length@notes}]]];
ResourceFunction["FunctionAudiolize"][func, {k, 0, Length@notes}, 0.4 * Length[notes], "MinFrequency" -> 440*2^(Min[notes] * 1/12), "MaxFrequency" -> 440*2^(Max[notes] * 1/12), "BaselineFrequency" -> 440*2^(Mean[notes] * 1/12)]]](https://www.wolframcloud.com/obj/resourcesystem/images/429/4295065b-b82a-468a-8365-6b597b3d2e48/212f87b4bf769395.png)