Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FullRankDecomposition

Source Notebook

Compute a full rank decomposition of a matrix

Contributed by: Jan Mangaldan

ResourceFunction["FullRankDecomposition"][m]

computes a full rank decomposition of the matrix m.

Details and Options

The result is given in the form {f,g} where f and g are matrices such that f.g==m.
In a full rank decomposition, the matrix m of dimension p×q is factored into a matrix f with dimensions p×r and a matrix g with dimensions r×q, where r is equal to MatrixRank[m].
The full rank decomposition is not unique; if f1.g1==m and f2.g2==m are two different decompositions of m, then there exists a matrix w with dimensions r×r such that f1==f2.w and w.g1==g2.
ResourceFunction["FullRankDecomposition"] takes the same options as RowReduce.

Examples

Basic Examples (3) 

Find a full rank decomposition of a rank-deficient matrix:

In[1]:=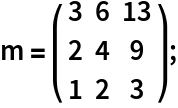
m = ( { {3, 6, 13}, {2, 4, 9}, {1, 2, 3} } );
In[2]:=
{fm, gm} = ResourceFunction["FullRankDecomposition"][m]
Out[2]=

Confirm the decomposition:

In[3]:=
m == fm . gm
Out[3]=

Format the factors:

In[4]:=
MatrixForm /@ {fm, gm}
Out[4]=

Scope (2) 

Find a full rank decomposition of a rectangular matrix with exact entries:

In[5]:=
m = {{1, 2, 3, 1, 0, 0}, {4, 5, 6, 0, 1, 0}, {7, 8, 9, 0, 0, 1}}; MatrixForm /@ ({fm, gm} = ResourceFunction["FullRankDecomposition"][m])
Out[6]=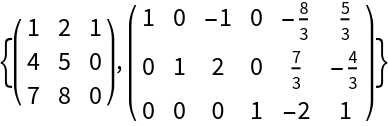

Confirm the decomposition:

In[7]:=
m == fm . gm
Out[7]=

Find a full rank decomposition of a complex matrix with inexact entries:

In[8]:=
m = RandomComplex[1, {3, 5}]; MatrixForm /@ ({fm, gm} = ResourceFunction["FullRankDecomposition"][m])
Out[9]=

Confirm the decomposition up to numerical rounding:

In[10]:=
m - fm . gm // Chop
Out[10]=

Version History

  • 1.0.0 – 25 January 2023

Source Metadata

  • Citation:
    • Piziak R., Odell, P.L., "Full Rank Factorization of Matrices." Mathematics Magazine, vol. 72, no. 3, 193-201, 1999.
      DOI: 10.1080/0025570X.1999.11996730

Related Resources

Author Notes

For numerical stability, FullRankDecomposition uses SVD when given a numerical matrix, and row reduction otherwise.

License Information