Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FullQRDecomposition (1.0.2) current version: 1.1.0 »

Source Notebook

Compute the full QR decomposition of a matrix

Contributed by: Jan Mangaldan

ResourceFunction["FullQRDecomposition"][m]

yields the full QR decomposition for a numerical matrix m. The result is a list {q,r}, where q is a unitary matrix and r is an upper‐trapezoidal matrix.

Details and Options

The original matrix m is equal to ConjugateTranspose[q].r.
q is always square, even for non-square m.
The matrix r has zeros for all entries below the leading diagonal, and has the same dimensions as m.
ResourceFunction["FullQRDecomposition"][m,Pivoting→True] yields a list {q,r,p}, where p is a permutation matrix such that m.p is equal to ConjugateTranspose[q].r.

Examples

Basic Examples (2) 

Compute the full QR decomposition for a 3×2 matrix with exact values:

In[1]:=
ResourceFunction["FullQRDecomposition"][{{1, 2}, {3, 4}, {5, 6}}]
Out[1]=
In[2]:=
Map[MatrixForm, %]
Out[2]=

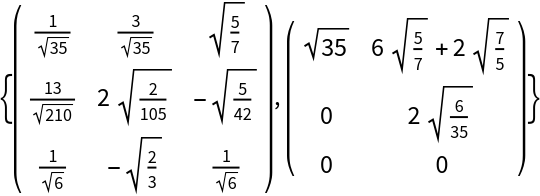
Compute the full QR decomposition for a 2×3 matrix with approximate numerical values:

In[3]:=
ResourceFunction["FullQRDecomposition"][{{1., 2., 3.}, {4., 5., 6.}}]
Out[3]=
In[4]:=
Map[MatrixForm, %]
Out[4]=

Scope (2) 

Use a 3×4 matrix:

In[5]:=
m = \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "2", "3", "4"}, {"1", "4", "9", "16"}, {"1", "8", "27", "64"} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\);

Full QR decomposition computed with exact arithmetic:

In[6]:=
ResourceFunction["FullQRDecomposition"][m]
Out[6]=

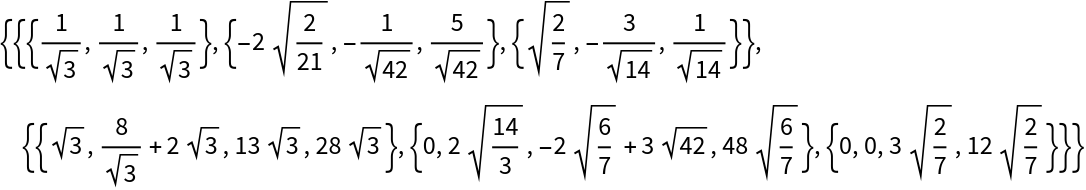
Full QR decomposition computed with machine arithmetic:

In[7]:=
ResourceFunction["FullQRDecomposition"][N[m]]
Out[7]=
In[8]:=
Map[MatrixForm, %]
Out[8]=

Full QR decomposition computed with 24-digit arithmetic:

In[9]:=
ResourceFunction["FullQRDecomposition"][N[m, 24]]
Out[9]=

Full QR decomposition for a 3×3 matrix with random complex entries:

In[10]:=
ResourceFunction["FullQRDecomposition"][ RandomComplex[{0, 1 + I}, {3, 3}]]
Out[10]=
In[11]:=
Map[MatrixForm, %]
Out[11]=

Options (5) 

Pivoting (5) 

Use a 3×4 matrix:

In[12]:=
m = \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "2", "3", "4"}, {"1", "4", "9", "16"}, {"1", "8", "27", "64"} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\);

Compute the full QR decomposition using machine arithmetic with pivoting:

In[13]:=
{q, r, p} = ResourceFunction["FullQRDecomposition"][N[m], Pivoting -> True]
Out[13]=

The elements along the diagonal of r are in order of decreasing magnitude:

In[14]:=
MatrixForm[r]
Out[14]=

The matrix p is a permutation matrix:

In[15]:=
MatrixForm[p]
Out[15]=

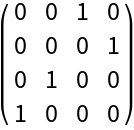
FullQRDecomposition satisfies m.p==ConjugateTranspose[q].r:

In[16]:=
ConjugateTranspose[q] . r - m . p // Chop
Out[16]=

Applications (5) 

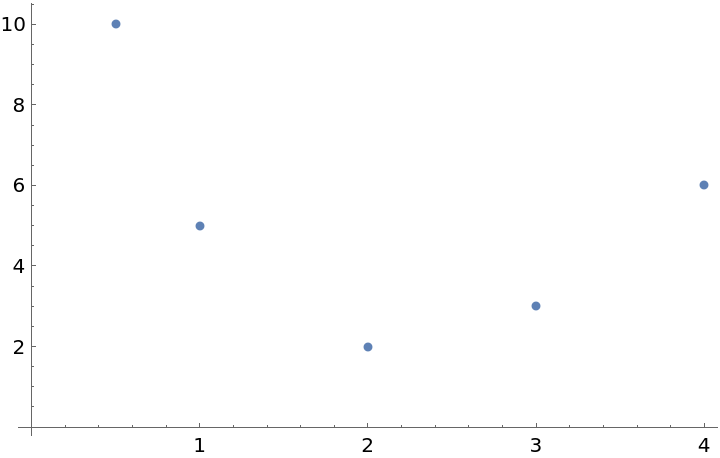
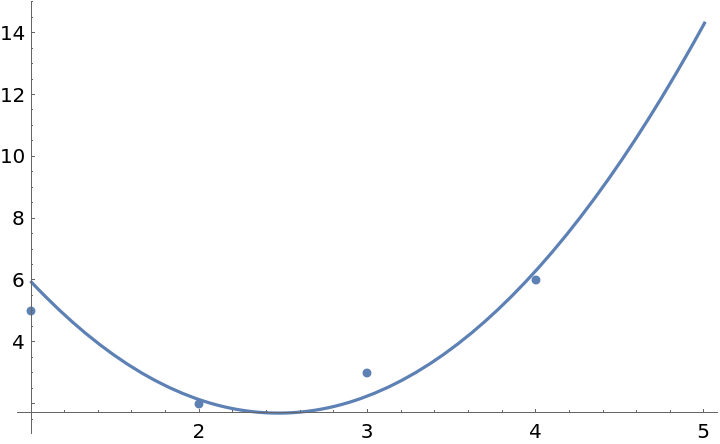
Here is some data:

In[17]:=
times = {1., 2., 3., 4., .5}; b = {5., 2., 3., 6., 10.}; data = Transpose[{times, b}];
In[18]:=
ListPlot[data]
Out[18]=

Set up a design matrix for fitting with basis functions 1, t, t2:

In[19]:=
m = DesignMatrix[data, {1, t, t^2}, t]
Out[19]=

Find the full QR decomposition of m:

In[20]:=
{q, r} = ResourceFunction["FullQRDecomposition"][m]
Out[20]=

This finds a vector x such that is a minimum:

In[21]:=
PseudoInverse[r] . q . b
Out[21]=

These are the coefficients for the least-squares fit:

In[22]:=
Fit[data, {1, t, t^2}, t]
Out[22]=
In[23]:=
Show[{Plot[%, {t, 1, 5}], ListPlot[data]}]
Out[23]=

Properties and Relations (5) 

Use a 3×4 matrix:

In[24]:=
m = \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "2", "3", "4"}, {"1", "4", "9", "16"}, {"1", "8", "27", "64"} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\);

Compute the full QR decomposition:

In[25]:=
{q, r} = ResourceFunction["FullQRDecomposition"][N[m]];

The rows and columns of q are orthonormal:

In[26]:=
Chop[q . ConjugateTranspose[q]]
Out[26]=
In[27]:=
Chop[ConjugateTranspose[q] . q]
Out[27]=

Check that r is upper trapezoidal:

In[28]:=
Dimensions[r] == Dimensions[m]
Out[28]=
In[29]:=
ArrayRules[r]
Out[29]=
In[30]:=
Cases[%[[All, 1]], {i_, j_} /; i > j]
Out[30]=

Check that m is equal to ConjugateTranspose[q].r:

In[31]:=
Chop[m - ConjugateTranspose[q] . r]
Out[31]=

Version History

  • 1.1.0 – 22 August 2022
  • 1.0.2 – 16 November 2021

Source Metadata

  • Citation:
    • Golub G.H., Van Loan C.F., Matrix Computations, Third Edition. Johns Hopkins University Press, Baltimore, pp. 223-236, 1996.

Related Resources

License Information